江苏2008年高考最后一题会有两个正确的答案吗

王美芳

（复旦大学附属中学，上海 200433）

这几年的各地高考卷涌现了很多好题，我们给学生进行高三复习时，常选来用.2008年江苏物理高考最后一题就是这样一道题，综合性强，对基本物理概念和能力要求都比较高，有相当的区分度.题目如下：

如图1所示，间距为L的两条足够长的平行金属导轨与水平面的夹角为θ，导轨光滑且电阻忽略不计.场强为B的条形匀强磁场方向与导轨平面垂直，磁场区域的宽度为d1，非磁场区域间距为d2.两根质量均为m、有效电阻均为R的导体棒a和b放在导轨上，并与导轨垂直.（设重力加速度为g）

图1

（1）若a进入第2个磁场区域时，b以与a同样的速度进入第1个磁场区域，求b穿过第1个磁场区域过程中增加的动能ΔEk；

（2）若a进入第2个磁场区域时，b恰好离开第1个磁场区域；此后a离开第2个磁场区域时，b又恰好进入第2个磁场区域.且a、b在任意一个磁场区域或无磁场区域的运动时间均相等.求b穿过第2个磁场区域过程中，两导体棒产生的总焦耳热Q；

（3）对于（2）问所述的运动情况，求a穿出第k个磁场区域时的速率v.

连续几年在高三复习时使用这道题，每次总会有个别学生提出异议并给出自己不同的解答.这道题，不同的思路考路，为什么得到的结果会不一样？是学生解答错了吗？其实，很多时候，学生的解题思路没有错.这时，我总是很耐心地帮学生看他的解答过程，肯定并鼓励他们的自主思考.笔者又到一些杂志和网上查找过这道题，也没有发现对本题多解的讨论.所以，写文一篇，希望有针对性地做一次充分的讨论，和大家一起分享思考的快乐.

本题的的第1问和第2问给出了一些信息，本文略去讨论它们，而矛盾在于第3问的求解.我们直接来解第3问.先看常规解法：

考虑其中一棒，如a棒，在经过d2区域的过程中，它做初速度为v1，末速度为v2，加速度为gsinθ，位移为d2的匀加速直线运动，设运动时间为t，可得

a棒，在经过d1区域的过程中，做减速运动，根据牛顿第二定律得

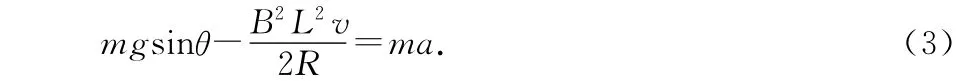
用微元法，考虑整个减速过程中任一Δt时间，并对时间做累加，由（3）式得

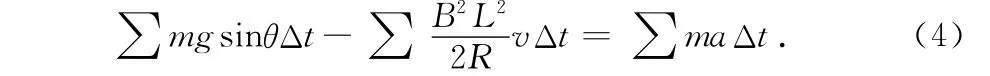
由（4）式得

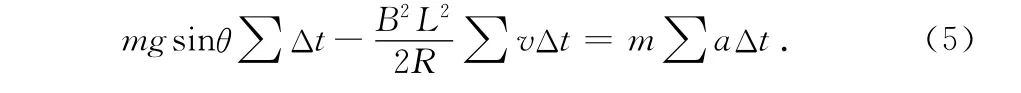
整理后得

（1）、（2）、（6）式是关于v1、v2、t这3个未知数的三元一次方程组，可解得

所以，第3小题要求的速率

解这道题的关键是通过微元法得到除（1）、（2）式外的另一个关于v1、v2、t的关系式，即上面的（6）式.如果按下面的解法，我们会发现根据题目条件，还可以得到另外一个不同于（6）式关系式.

同样考虑a棒减速过程：前面已经给出

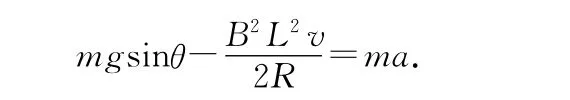
对这个式子，做另一种处理：因为a＝dv，所以（3）式dt可化为

两边分别对速度和时间积分

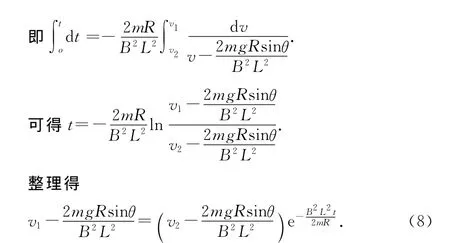
这样就得到了又一个不同于（6）式的v1、v2、t之间的关系式，即（8）式.由（1）、（2）、（8）式可得

所以，本题第3小题要求的速率

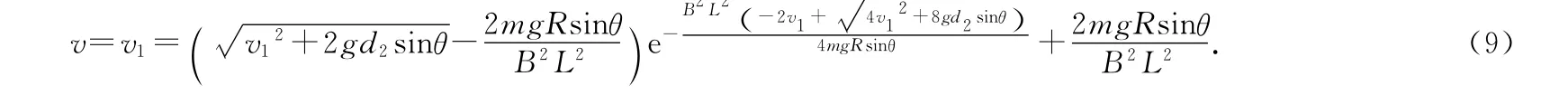
（9）式虽然不像参考答案（7）式那样简洁，但也是实实在在能做出来的一个正确答案.

有必要对两个答案都是正确的做进一步的说明.根本原因是题目中给的条件多了，不完全独立.这就好比平抛运动同时告诉初速度v0，高度h，射程s，求飞行时间t.答案就不唯一了，可以是也可以.因为v0，h，s不相互独立，知道其中2个就能推算出第3个，所以题目本不应该给3个已知条件.这个例子中3个量的不相互独立非常容易看出来，但本题中的已知量之间不相互独立不是那么显而易见，可以说是隐蔽得非常深，猛一眼完全看不出来，但可以通过以下计算得出.

假设本题中没有给出磁场区域的宽度为d1这个条件，而其他已知条件都不变，可以这样计算出d1.

同样考虑a棒减速过程：前面已经给出

两边分别对距离和速度积分

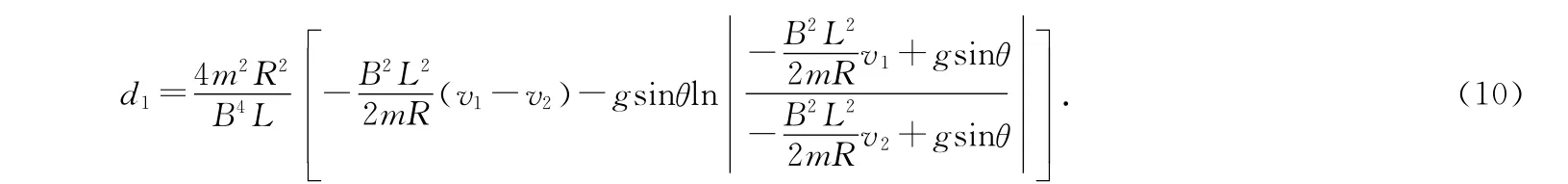
利用积分公式

这样（1）、（2）、（6）、（10）4式构成了关于v1、v2、t、d1四元一次方程组，可求得v1、v2、t、d1.也就是说，本题中d1不是独立变量，条件给多了.

从学生的角度来讲，程度好的学生可能会发现他做的答案和标准答案不一样，但很可能找不出来错在哪里.我也曾今看到有的学生拿着不一样的答案问教师，教师的回答是：“反正正确答案不是你这个答案！你就按正确答案来做！”希望这篇文章能帮助到大家理解这个问题，希望我们的学生遇到问题能坚持追根究底.