基于改进ORB 算法的遥感图像自动配准方法

张云生，邹峥嵘

(中南大学地球科学与信息物理学院，长沙 410083)

0 引言

遥感图像配准是实现图像融合、变化检测、图像纠正和图像镶嵌等应用的一个关键步骤。遥感图像自动配准方法大致可以分为2 类:①基于区域的整体配准方法。如基于相关系数、互信息或者相位相关的方法［1－2］，这类方法耗时较长;②基于特征的配准方法。近年来，随着计算机视觉领域中尺度不变特征变换(scale－invariant feature transform，SIFT)和加速鲁棒性特征(speeded up robust features，SURF)等具有尺度和旋转不变性算子的兴起，这2种算法在遥感图像配准中的应用引起了众多学者的关注，并取得了较好的效果［3－5］。但SIFT 和SURF算法要求建立高维描述符，需要大量的内存空间和较长的运行时间。Calonder 等［6］提出了一种基于二进制的鲁棒性独立基本特征(binary robust independent elementary features，BRIEF)描述符，大大缩短了建立描述符的时间，同时减少了对存储空间的需求，而且对光照变化具有较强的鲁棒性;但是其特征点检测不具备尺度和旋转不变性。在此基础上，Rublee 等［7］提出了定向二进制简单描述符(oriented brief，ORB)算法，在图像金字塔上利用加速分割测试特征(features from accelerated segment test，FAST)算子提取角点特征，使得特征点具有一定程度的尺度不变性;然后计算出角点的主方向，建立BRIEF描述符，使得描述符具有旋转不变性。ORB 算法提高了运算的适应性，在标准数据集中取得了可与SURF 算法和SIFT 算法相媲美的效果，但运算速度比SURF 算法快了1个数量级、比SIFT 算法快了2个数量级［8］。李慧等［9］提出利用FAST 算法检测角点、利用SURF 算法匹配获取控制点，但处理效率依然受到SURF 算法的影响。针对上述情况，本文提出利用结合随机采样一致性(random sample consensus，RANSAC)方法［10］的改进ORB 算法为遥感图像配准提供控制点，实现遥感图像自动配准。

1 配准方法

1.1 配准流程

配准是寻找一个从待配准图像到参考图像的变换参数，并将待配准图像纠正到参考图像坐标系的过程。本文提出的基于改进ORB 算法的遥感图像自动配准流程如图1 所示。

图1 基于改进ORB 算法的遥感图像自动配准流程Fig.1 Flow chart for automatic registration of remote sensing images based on improved ORB algorithm

上述配准流程主要由如下3个步骤组成:

1)初始控制点匹配。在参考图像和待配准图像上分别提取特征点并建立二进制描述符，然后利用局部敏感散列(locality sensitive hashing，LSH)算法匹配这些二进制描述符［11］。

2)控制点优化。利用RANSAC 算法，结合单应性矩阵估计，剔除可能的错误匹配。

3)图像纠正。利用最小二乘法估计单应性矩阵，并对待配准图像进行重采样。

1.2 初始控制点匹配

1.2.1 特征点提取

ORB 算法采用FAST 算子检测角点，但原始FAST 算子在边缘上也会提取到大量特征点，因此ORB 算法计算了FAST 所提取局部特征点的Harris兴趣值(即角点响应值)，并按兴趣值大小进行排序;然后根据特征点数目的需求，保留兴趣值较大的N个点。FAST 算子虽然具有一定程度上的尺度不变性，但由于没有提供特征点所对应的尺度，因此在后续处理中难以建立具有尺度不变性的描述符。ORB 算法为了减轻尺度的影响，通过在多层金字塔图像中提取特征点来获取尺度信息，以用于建立后续处理中的描述符;但在利用Harris 兴趣值大小排列特征点时，分布情况易受到图像纹理的影响——在图像纹理丰富区域容易提取到大量特征点，反之则提取到的特征点较少。当特征点分布不均匀时，同名点容易被集中到图像的局部区域，使用局部同名点对整景图像进行配准时，整体精度会受到很大的影响。

针对ORB 提取特征点不均匀的问题，本文提出一种基于格网滤波的改进的ORB 特征点提取方法，即在利用FAST 算子提取特征点之后，再对每个特征点计算Harris 兴趣值;在此基础上，将整景图像划分为格网大小为n×n 的均匀格网，然后在每个格网中保留兴趣值最大的特征点。

要建立稳定(reliable)和独特(distinctive)的描述符，需要确定特征点的尺度和主方向;通过对主方向的旋转，可使描述符具有旋转不变性。SIFT 和SURF 算法采用了基于梯度直方图的方法获取特征点的主方向，但存在主方向不唯一的缺点;因此，ORB 算法采用亮度中心(intensity centroid)来计算特征点的主方向。通过比较，ORB 算法具有较好的适应性。

在获取特征点尺度和主方向的基础上，采用BRIEF 描述符的思想建立描述符，但同时顾及特征点的尺度和主方向。在特征探测的基础上，对每个特征点建立由(0，1)组成的n 维二进制描述符;本文中取n=256，因此对于每个特征点会得到一个256 bit 的描述符。

1.2.2 特征点匹配

在建立二进制描述符之后，要进行特征匹配，通过比较描述符的相似性即可实现。对于2个二进制描述符的相似性，可以使用汉明距离(hamming distance)来表示。汉明距离(将一个字符串变换成另外一个字符串所需要替换的字符个数)的计算使用按位“异或”运算实现，即参与运算的2个值，如果它们的相应bit 相同，则结果为“0”，否则为“1”;然后统计“1”的个数，“1”的个数越少，表示2个二进制描述符越相似。对于256 bit 的2个二进制描述符，汉明距离取值在0～256 之间的，难以使用一个合适的阈值去确定正确的匹配。因此，本文以近邻距离与次近邻距离的比值T 来确定可能正确的匹配，只有当T ＜0.8 时，才认为最近邻距离对应的特征点有可能为同名点。

当图像存在有重复纹理或者遮挡问题时，特征匹配获取的同名点可能存在错误匹配点。因此，本文在进行了一次从左到右的图像匹配之后，再进行一次从右到左的匹配，只保留在2个方向上相一致的图像匹配结果。

对于图2(a)和(b)所示的一组卫星光学遥感图像(大小均为512 像元×512 像元，编号分别为b040 和b042)，每景图像都提取3 000个特征点，经过匹配之后，获取789个同名点，匹配结果如图2(c)所示。

图2 初始控制点匹配结果Fig.2 Matching result of initial control points

从图2 可以看出，大部分同名地物点都是匹配正确的，只有少量匹配错误的点。

1.3 控制点优化

透射变换是一种常用于表达图像之间变换关系的模型。本文采用基于单应性矩阵(homography matrix，即用于图像纠正和配准的线性变换矩阵)的透射变换表示图像之间的关系，变换式为

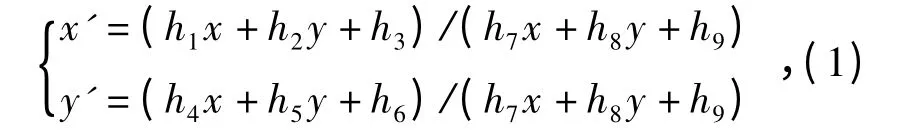
式中:x，y 分别为待配准图像的列、行坐标;x'，y'分别为参考图像的列、行坐标;hi(i=1，2，…，9)为2景图像之间的变换参数。

尽管在初始控制点匹配阶段采用了双向匹配，但依然会存在少量的错误匹配点，如果不加以剔除，将会对配准结果有较大的影响。因此，本文采用基于RANSAC 算法、结合单应性矩阵估计的方法予以剔除，保留误差小于2个像元的控制点作为优化后的控制点。图2(c)所示的789个初始控制点匹配结果，经过上述优化后，获取392个控制点的匹配结果(图3)。

图3 优化控制点的匹配结果Fig.3 Matching result of optimized control points

1.4 图像纠正

经过控制点优化之后，还存有大量的同名点，多于单应性矩阵计算所需要的4个同名点，因此采用最小二乘估计来计算单应性矩阵。最后，待配准图像中的所有像元根据单应性矩阵变换参数纠正到参考图像的坐标下。为了平衡纠正的精度和效率，本文在图像纠正中采用双线性插值对图像进行重采样。图4 是采用根据图3 所示控制点计算的单应性矩阵进行图像纠正的结果。

图4 图像纠正结果Fig.4 Result of image rectification

2 试验分析

为了验证本文方法对不同类型遥感图像配准的适应性，采用了2 组卫星光学遥感图像(数据来源于http:// nayana.ece.ucsb.edu/ registration/)和1 组SAR 图像进行配准试验。

2.1 卫星光学遥感图像配准

图2(a)为图像b040，大小为512 像元×512 像元，作为参考图像;图2(b)为图像b042，大小也是512 像元×512 像元，作为待配准图像。采用本文方法将待配准图像配准到参考图像上，配准结果如图5 所示。

图5 b040 与b042 图像配准结果Fig.5 Registration result between b040 and b042

为了更直观地显示配准情况，将配准后的图像与待配准图像一起显示，对2 景图像相交部分利用马赛克方式交错显示，并将图5(a)中黑色方框内部分放大显示(图5(b))。从图5(b)可以看出，配准后的影像边缘能够保持较好的连续性，表明2 景图像得到了较好的配准。

用同样方法，对另1 组Landsat TM 图像进行了配准(图6)。参考图像(图6(a))和待配准图像(图6(b))分别为Landsat TM 的2个波段图像，通过本文方法配准后的结果如图6(c)所示，对其中黑色方框内部分放大显示结果如图6(d)所示。由图6(d)可以看出，2个波段的图像得到了精确的配准。

图6 TM 图像配准结果Fig.6 Registration result between TM images

2.2 SAR 图像配准

为了进一步验证本文方法的有效性，还采用了如图7(a)和(b)所示的2 景SAR 图像进行配准试验，配准结果如图7(c)所示，图7(c)中黑框内部分放大结果如图7(d)所示。从图7(d)可以看出，本文方法将2 景SAR 图像自动配准到了一起。

图7 SAR 图像配准结果Fig.7 Registration result between SAR images

2.3 与SIFT 和SURF 的比较

为了比较不同算法的配准结果，使用SIFT［12］和SURF［13］算法对上述3 组试验数据提取特征，并且利用Low［12］的比值方法进行控制点匹配，比值阈值设置为0.8。获取控制点后，将控制点平分为2 组，一组用于计算单应性矩阵，另一组用于精度检查。利用检查点统计了最大残差(Max)和均方根误差(RMSE)，并对每种算法的控制点匹配数目和时间都进行了比较。比较结果如表1 所示，其中“配准时间”是使用笔记本电脑(配置为intel i3 CPU，2.40GHZ，2.00 G RAM，操作系统32－ bit Window 7)试验的结果。

从表1 中3 种算法匹配结果的比较可以看出，本文方法比基于SURF 算法和SIFT 算法的配准方法效率高。对于光学遥感图像而言，本文方法的配准精度略低于基于SIFT算法的配准精度，但基于SIFT 算法的配准效率最低;对于SAR 图像而言，本文方法无论在配准效率上还是在配准精度上都优于基于SURF 和SIFT 算法的配准方法。

表1 配准结果比较Tab.1 Comparison of registration results

3 结论

本文提出了一种基于改进的定向二进制简单描述符(ORB)算法的遥感图像配准方法，并选取具有代表性的卫星光学遥感图像对和SAR 图像对进行了试验。根据试验结果可以得出以下结论:

1)本文方法可以提取足够控制点实现遥感图像自动配准，能够获取亚像元级的配准精度，与基于SIFT 算法和SURF 算法的配准精度相当或者更高。

2)本文方法在效率上比基于SIFT 算法和SURF算法的配准效率有大幅度的提高。

下一步的工作将研究如何进一步提高基于ORB 算法的图像配准精度。

［1］Kern J P，Pattichis M S.Robust multispectral image registration using mutual－information models［J］.IEEE Transactions on Geoscience and Remote Sensing，2007，45(5):1494－1505.

［2］韦春桃，吴 平，张祖勋，等.一种改进的相位相关的影像配准方法［J］.测绘通报，2011(4):19－22.Wei C T，Wu P，Zhang Z X，et al.An image matching algorithm based on improved log－polar image transform［J］.Bulletin of Surveying and Mapping，2011(4):19－22.

［3］Liu X Z，Tian Z，Chai C Y，et al.Multiscale registration of remote sensing image using robust SIFT features in steerable－domain［J］.The Egyptian J Remote Sensing and Space Sci，2011，14(2):63－72.

［4］李晓明，郑 链，胡占义.基于SIFT 特征的遥感影像自动配准［J］.遥感学报，2006，10(6):885－892.Li X M，Zhen L，Hu Z Y.SIFT based automatic registration of re-motely－sensed imagery［J］.Journal of Remote Sensing，2006，10(6):885－892.

［5］林晓帆，林立文，邓 涛.基于SURF 描述子的遥感影像配准［J］.计算机工程，2010，36(12):216－218.Lin X F，Lin L W，Deng T.Remote sensing image registration based on SURF gescriptor［J］.Computer Engineering，2010，36(12):216－218.

［6］Calonder M，Lepetit V，Ozuysal M，et al.BRIEF:Computing a local binary descriptor very fast［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2012，34(6):1281－1298.

［7］Rublee E，Rabaud V，Konolige K，et al.ORB:An efficient alternative to SIFT or SURF［C］//2011 International Conference on Computer Vision，Barcelona，Spain，2011:2564－2571

［8］Rosten E，Drummond T.Machine learning for high－speed corner detection［C］//Lecture Notes in Computer Science，2006，3951:430－443.

［9］李 慧，蔺启忠，刘庆杰.基于FAST 和SURF 的遥感图像自动配准方法［J］.国土资源遥感，2012，24(2):28－33.Li H，Lin Q Z，Liu Q J.An automatic registration method of remote sensing imagery based on FAST corner and SURF descriptor［J］.Remote Sensing for Land and Resources，2012，24(2):28－33.

［10］Fischer M A，Bolles R C.Random sample consensus:A paradigm for model fitting with applications to image analysis and automated cartography［J］.Communications of the ACM，1981，24(6):381－395.

［11］Marius M，Lowe D G.Fast approximate nearest neighbors with automatic algorithm configuration［C］//International Conference on Computer Vision Theory and Applications，Lisboa，Portugal，2009:331－340.

［12］Lowe D G.Distinctive image features from scale－ invariant keypoints［J］.International Journal of Computer Vision，2004，60(2):91－110.

［13］Bay H，Ess A，Tuytelaars T，et al.Speeded－ up robust features(SURF)［J］.Computer Vision and Image Understanding，2008，110(3):346－359.