基于遗传算法的塔式起重机定位和防摆研究

游谊，胡伟，张自强，曾经宇，熊彤

(上海师范大学信息与机电工程学院，上海201418)

0 引言

随着建筑业的发展，塔机是建筑施工的主要运输机械。在搬运过程中，由于会受到外界因素的影响(如风力和摩擦力)以及操作人员工作经验的限制，会引起小车定位不准确和负载摆动幅度大等问题，势必会影响工作效率，给施工人员带来安全隐患。因此有必要研究起重机快速对位和消除摆动的方法。［1－2］以往控制算法多采用模糊PID控制，虽然在处理复杂系统如塔式起重机这样的大时滞性、时变及非线性系统时，显示出一定的优越性，但简单的模糊控制在复杂系统的控制中仍表现出诸多的局限性。如在系统调试过程中需花费很长时间去调整隶属函数与控制规则以达到良好的控制效果。［3－4］与模糊PID控制相比，遗传算法不需要编辑复杂的控制规则，避免了前期大量规则库整理工作和仿真实验。文中采用遗传算法对起重机对位和防摆问题进行分析，实验结果表明该方法的可行性和有效性。

1 塔式起重机的数学模型

起重机防摆系统是一个典型动力学系统，根据其力学特性，采用分析力学中拉格朗日方程来建立起重机防摆系统的数学模型。［5－6］塔式起重机简化模型如图1所示。

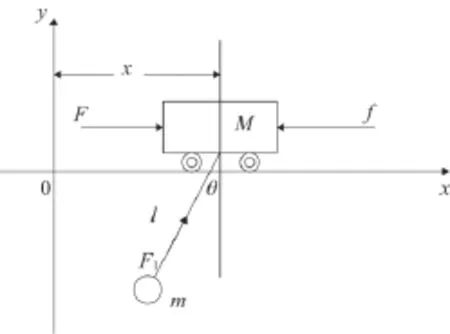
图1 起重机简化模型

根据拉格朗日方程对起重机防摆系统进行受力分析可得：

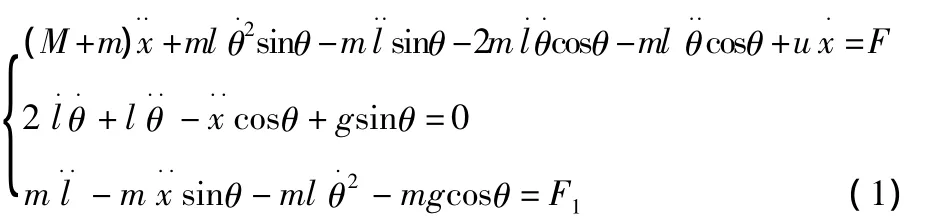
式中：M为小车质量;m为负载质量;l为悬绳的绳长;θ为悬绳摆角;系统受到的外力有小车驱动力F，钢丝绳起升力F1，小车与轨道之间的摩擦力f。由于本文研究塔吊负载水平运动过程中消摆控制，不考虑负载的提升，即绳长不变的情况。所以：

可得到定绳长的起重机防摆系统的数学方程为：

由于吊车运行中摆角不会超过10°，且平衡位置时θ=0，式(1)进一步简化得：

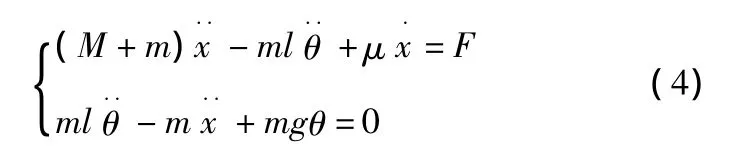
本文实验的目的是在给定一个行走距离参考值的情况下，牵引小车安全到达指定位置，并且消除负载摆动。也就是说根据给定的小车行走距离和反馈回来负载摆角信号，通过控制算法计算输出相应的电信号给驱动电机，控制小车带动负载快速到达指定位置，同时做到悬绳摆角消减为零。

2 遗传算法与模糊控制

2.1 模糊控制主要特点

模糊控制是对难以用已有规律描述的复杂系统，［7－10］采用基于自然语言控制规则，模糊推理的计算机控制技术，它不依赖与控制系统的数学模型，而是依赖于操作过程中人员控制经验归纳成定性描述的一组条件语句，［11－13］然后运用模糊集合理论将其量化为模糊语言集，从而构成控制算法。［14－15］模糊PID定位防摆控制系统的仿真框图如图2所示。

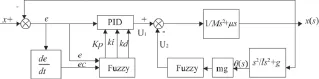
图2 模糊PID控制器的结构

2.2 遗传算法基本原理

遗传算法(GA)是美国Michigan大学Holland教授提出的模拟自然界遗传机制和生物进化论的一种并行搜索最优化办法。它将“优胜劣汰，适者生存”的生物进化原理引入优化参数形成的编码串群体中，按照所选择的适配值函数并通过遗传中的幅值，交叉及变异对个体进行筛选，使适配值高的个体被保留下来，组成新的群体，新的群体既继承了上一代的信息，又优于上一代。这样周而复始，群体中个体适应度不断提高，直到满足条件。［16］文中用于起重机定位和防摆的算法，就是基于遗传算法提出的，再结合工业控制中应用广泛的PID算法，组成遗传算法优化的PID整定，即可实现对PID参数的最佳调整，因此可以被用于塔式起重机的自动控制中。其整定原理如下所示。

1)参数确定及表示

首先确定参数范围，然后根据精度的要求，对其进行编码。选取二进制字串来表示每一个参数，并建立与参数间的关系。

2)选取初始种群

由计算机随机产生初始种群。例如：针对二进制编码而言，先产生0－1之间均匀分布的随机数，然后确定产生的随机数0－0.5之间代表0，0.5－1之间代表1。另外根据计算的复杂程度确定种群大小。

3)适配函数的确定

为了防止控制信号过大，系统出现不稳定，又不因控制量过小，造成系统响应时间过长，就需要控制量，误差，上升时间作为适配函数的约束条件。这是因为适配函数与目标函数相关，最优控制的参数也就是在满足约束条件下使f(y)最大时，y对应的控制器参数。

4)遗传算法的操作

首先利用适度值比例法进行复制。即通过适配函数，进而求每个串对应的复制概率。复制概率与每代字串的个数乘积为该字串在下一代中应复制的个数。复制概率大的在下一代中将有较多的子代，相反的被淘汰。其次进行单点交叉、交叉概率为Pc。从复制后的成员里以Pc概率选取字串组成匹配池，然后随机对匹配池成员匹配，交叉位置随机确定。最后以概率Pm进行变异。初始种群通过复制、交叉及变异得到新一代种群，该种群经解码后代入适配函数，观察是否满足结束条件，若不满足，则重复以上操作指导满足为止［16］。

3 遗传算法流程图

利用遗传算法优化Kp、Ki、Kd的具体步骤如下：

1)确定每个参数的大致范围，进行编码;

2)随机产生n个个体构成初始种群P(0);

3)将种群中各个体解码成对应的参数值，用此参数求代价函数值J及适应函数值f，取f=1/J;

4)应用复制、交叉、变异算子对种群P(t)进行操作，产生下一代种群P(t+1);

5)重复步骤3)和4)，直至参数收敛或达到预期目标。

遗传算法流程图如图3所示。

图3 遗传算法流程图

4 仿真实验与分析

为了验证算法的可行性，对基于遗传算法的PID控制进行了仿真实验，与模糊PID算法相比，仿真结果表明了该方法的可行性和良好的控制效果。塔式起重机模型参数：小车质量M=3 kg，负载质量m=0.2 kg，绳长l=1 m，位移X=3 m。遗传算法中使用的样本个数为Size=30，交叉概率和变异概率分别为：Pc=0.90，Pm=0.033。为了防止遗传算法寻优区域局部最优解，采用保留最优个体法。经遗传算法优化后所得到的三个参数的数值分别为：kp=7.851 2，ki=0.220 9，kd=2.850 9。仿真结果如图3，图4，图5，图6所示。

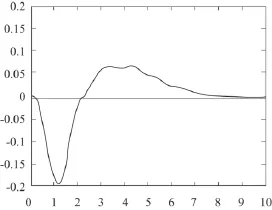
图3 模糊PID控制位移曲线

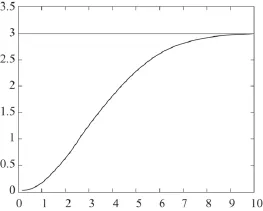
图4 模糊PID控制位移曲线

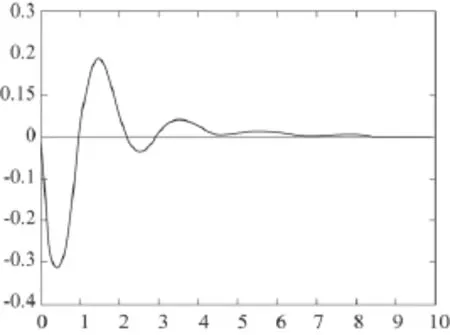
图5 遗传算法PID控制摆角曲线

图6 遗传算法PID控制位移曲线

在相同的实验条件下，图3和图4给出了采用模糊PID控制的仿真结果。图5和图6是遗传算法优化的PID控制摆角位移曲线。通过对比可以得到，基于遗传算法PID整定的摆角曲线在5 s内几乎减小至零，衰减速度优于模糊PID算法3 s左右;位移曲线在7 s时到达指定位移，与模糊PID位移曲线的响应时间相比提高了3 s左右。从仿真图中可以看出基于遗传算法的PID控制，在准确对位和快速消摆上更胜一筹，用于建筑施工时更有利于防止事故的发生。

5 结语

文中对塔式起重机定位和防摆进行了研究，采用遗传算法优化PID参数，它具有操作方便，速度快的优点。不需要复杂的规则，只通过简单的复制、交叉及变异，便可以达到寻优，避免前期大量整理工作，为实现复杂系统的控制提供了有效途径，同时也提高了稳态精度和收敛速度，在实现起重机定位和快速消摆的问题上，取得良好的控制效果。

［1］马晓虹.一种模糊自适应PID控制器的设计［J］.大庆师范学院学报，2009，29(3)：37-39.

［2］李伟.基于时间最优的起重机消摆控制策略［J］.山东工业大学学报，1998，28(2)：107-111.

［3］华克强.桥式吊车模糊防摆技术［J］.中国民航学院学报，2000，18(3)：12-15.

［4］薛朵，李宇成.港口集装箱吊车的建模与模糊控制［J］.机电一体化，2009，31(2)：28-32.

［5］薛定宇，陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用［M］.北京：清华大学出版社，2003.

［6］樊京，刘叔军，盖晓华，等.MATLAB控制应用与实例［M］.北京：清华大学出版社，2008.

［7］姜兴华，尹志宇，郭晴.一种模糊自整定PID控制器的设计与仿真［J］.河北师范大学学报(自然科学版)，2009，33(4)：448-450.

［8］曾光奇，胡均安，王东，等.模糊控制理论与工程应用［M］.武汉：华中科技大学出版社，2006.

［9］张静等.MATLAB在控制系统中的应用［M］.北京：电子工业出版社，2007.

［10］席爱民.模糊控制技术［M］.西安：西安电子科技大学出版社，2008.

［11］王正林，王胜开，陈国顺.MATLAB/Simulink与控制系统仿真［M］.北京：电子工业出版社，2005.

［12］蒋理，陈树广.基于模糊控制的桥式起重机定位防摆研究［J］.计算机仿真，2009，26(6)：179-182.

［13］但堂咏.岸边桥式起重机智能防摇机理研究［D］.武汉：武汉理工大学，2005.

［14］王宏，黎亚元，陈守强，姚悠然.起重机模糊控制系统的研究［J］.机电工程技术，2006，35(9)：18-20.

［15］石辛民，郝整清.模糊控制及其MATLAB仿真［M］.北京：清华大学出版社，2008.

［16］刘金琨.先进PID控制及其 Matlab仿真(第2版)［M］.北京：电子工业出版社，2005.