某高低压榴弹发射器两相流内弹道数值模拟

方磊磊，周克栋，赫雷

(南京理工大学机械工程学院，江苏南京210094)

0 引言

榴弹发射器可毁伤开阔地带及野战掩蔽工事内的有生目标和轻型装甲目标，压制敌火力点，摧毁其技术兵器和设施，可用于打击薄壁装甲目标或执行其他战斗任务，同时也是重要的警用防暴武器［6］。当高低压发射原理成功应用在美国40 mm榴弹时，人们予以了很高的评价，并迅速在世界范围内得到推广。通过高低压药室结构参数和装填条件的改变，来研究控制高压室和低压室的压力，以及弹丸的初速的规律［1］。

1 榴弹发射时的物理模型

底火被机械击发，先引燃附近发射药，由它所产生的炽热气体和固体产物进而引燃周围更多发射药。高温高压的气体和炽热固体粒子的对流和辐射使得药床逐次被点燃，形成火焰阵面的传播［2］。在压力阵面向前传播的同时，若气体压力超过铜质衬片的剪切强度，喷孔被打开，气体压力由高压室传入低压室。当低压室压力升至弹丸启动压力后，弹丸开始做加速运动。

榴弹发射时，其等效物理模型示意图如图1所示。

图1 榴弹发射等效物理模型

根据以上高低压榴弹发射过程的物理化学现象，提出以下基本假设［3］：

1)单个颗粒火药都服从几何燃烧定律和指数燃速定律，火药的几何形状和尺寸是严格一致的;

2)火药的燃烧产物的组分保持不变，火药气体的热力参数，如火药力、余容及绝热指数均保持为常量;

3)固体药粒不可压缩，即火药的物质密度为常数;

4)火药燃气服从诺贝尔－阿贝尔方程;

5)对于阻力、热传导及燃烧等微观过程，假定作为两相当地平均状态的函数。

2 数学模型

2.1 基本方程［3］

将气相能量方程、气固两相连续方程和动量方程写成守恒的形式：

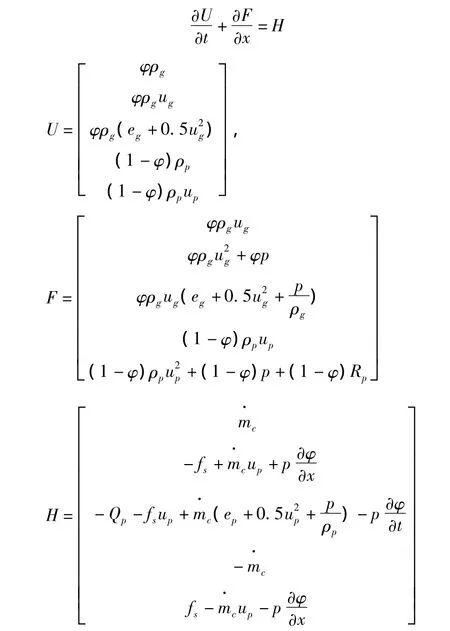
式中，φ 为空隙率，ρg、ug、eg分别为气相的密度、速度、内能，ρp、up、ep分别为固相的密度、速度、内能，fs为相间阻力，Qp为相间热交换量，p为气相压力，m·c为固体颗粒燃烧生成气体质量。

2.2 辅助方程

辅助方程包括相间阻力、相间热交换、状态方程、火药燃烧速率、形状函数、颗粒间应力和火药表面温度的方程，具体参见文献［4］。

另外需要说明的是：1)火药着火准则采用的是固相点火理论模型，火药颗粒表面温度达到点火温度时，火药即被点燃，火药着火温度取565 K;2)高低压室之间的衬片材料为黄铜A62，经计算破膜压力为105 MPa。

2.3 差分格式及定解条件

1)差分格式

对于上述基本方程，本文采用MacCormack差分格式进行数值求解，具体形式如下：

稳定性条件见文献［5］。

2)初始条件

初始条件的确定根据装填条件确定，但对于有装药间隙的情形一般在保证装药量不变的条件下可以适当抹平。使用的是M9发射药的相关示能参数，高压室容积V1=7.85 ×10－7m3，低压室初始容积V2=1.49 ×10－5m3。

3)边界条件

左边界：不考虑后坐的影响，可以把膛底当作静止的固壁，即ug(0，0)=up(0，0)=0，采用第二网格系中的反射法。

右边界：在低压室未达到启动压力时，右边界也是固定边界。但是当弹丸运动后，采用运动控制体方法，推导出守恒格式即可［3］。

3 结果与分析

忽略弹丸挤进过程的影响，用该模型计算后，得到高压室膛底最大膛压值约为247 MPa，低压室最大压力点约为19.6 MPa，与实测值符合较好，如图2所示高压室膛底压力变化曲线。

图2 高压室膛底压力曲线

从图3不同时刻压力随空间分布曲线可以看出，在弹丸未运动之前，膛内存在压力梯度，当弹丸运动后，膛内压强平缓下降。

图3 不同时刻压力分布曲线

由图4不同时刻气相速度随空间分布曲线可以看出，弹丸没有运动之前，气相速度波动较大，随着弹丸的运动，气相速度逐渐呈现上升趋势。

图4 不同时刻气相速度曲线

从图5不同时刻固相速度随空间分布曲线可以看出，弹丸没有运动之前固相速度波动也较大，在弹底处固相速度较小，是因为弹底处聚集的颗粒比较多，弹丸的运动，固相颗粒速度呈现与气相速度类似的特性。

图5 不同时刻固相速度曲线

从图6不同时刻空隙率分布曲线可以看出，弹丸没有运动之前，由于火药颗粒不断向右的运动，从而导致右边的火药颗粒比较密集，左端比较稀疏，即左端空隙率较大，而右端空隙率较小。火药全面着火后，空隙率逐渐上升，当弹丸运动后，弹底空隙率较高，这是因为固相颗粒速度没有弹丸速度大，从而在弹底存在一个纯气相区，火药全部燃烧完后，空隙率接近于1。

4 结语

1)在提出榴弹发射器发射的等效物理模型的基础上建立了其内弹道一维两相流模型，并运用该模型模拟了任意时刻、枪膛任意位置的压力变化规律，以及燃气和火药颗粒的运动规律，计算结果与实验测量结果吻合较好。

图6 高压室膛底曲线

2)对气固两相都采用了二阶精度MacCormack两步差分格式，并运用该格式完成了模型的VB编码计算，便于后续开发具有良好人机交互界面的内弹道软件。

3)由计算结果可以看出，利用高低压原理发射榴弹过程中内弹道各参数的变化规律与传统枪炮武器内弹道过程的变化规律基本上一致，而且能实现“高初速、低后坐力”的目的。

［1］刘寅.某新型防暴榴弹发射器方案设计与仿真研究［D］.南京：南京理工大学，2012：1～3.

［2］解放军总参谋部轻武器论证研究所.步兵近战武器论证参考［M］.北京：国防工业出版社，1992：160～175.

［3］金志明，袁亚雄，宋明.现代内弹道学［M］.北京：北京理工大学出版社，1992.

［4］翁春生，王浩.计算内弹道学［M］.北京：国防工业出版社，2006：65～94.

［5］金志明，袁亚雄.内弹道气动力原理［M］.北京：国防工业出版社，1983.

［6］袁亚雄，张小兵.高温高压多相流体动力学基础［M］.哈尔滨：哈尔滨工业大学出版社，2005.