高气液比气井管流压降计算实用方法

李颖川 刘 通 钟海全 张 坤 王 涛 侯朋军 张国兄

1．“油气藏地质及开发工程”国家重点实验室·西南石油大学 2．中国石油西南油气田公司川中油气矿3．胜利油田鲁明油气勘探开发有限责任公司 4．中国石油华北油田公司第二采油厂

气井生产动态分析和排液工艺设计等都离不开气井气液两相管流压降计算［1－3］。目前气液两相管流模型主要分为机理模型和经验模型。机理模型是目前描述两相流最精细的手段［4－5］，然而其精度同时取决于流型划分的精度、流型间的连续性和压降计算方法本身，同时计算比较复杂［6］。经验模型简单、连续且具有与机理模型相当的精度［7－9］，而阻力系数法是经验模型中最为简单实用的一种［10］。

阻力系数法将气液两相流动规律反映于阻力系数中，通过查询阻力系数图版实现两相流的计算，最早的代表 是 Poettmann－Carpenter 图 版［11］和 Baxendall－Thomas图版［12］。后来 Fancher－Brown［13］将阻力系数法推广到更宽的气液比（GLR）范围。但主要是针对油井条件提出的且图版中的横坐标为英制单位下密度、流速、管径的乘积，不便于使用。Tek［14］、陈家琅［15］改进了阻力系数图版的适应性，采用了不含量纲的两相雷诺数作为图版横坐标，但他们的回归数据仍主要来自油井，仅适用于较低的气液比范围。因此以气井实测压力数据为基础，引入无因次两相雷诺数的概念，拟合阻力系数与两相雷诺数的关系，进而修正两相雷诺数，绘制了适用于高气液比气井条件的阻力系数新图版。

1 气井压力梯度方程

气井气液两相管流可视为沿井深z方向的一维稳定流动。基于质量和动量守恒原理，其压力梯度方程可表示为重力、摩阻和动能三项压力梯度之和［16］，即

考虑在高气液比下流型多为环状流，液滴与气体流速相近，气液滑脱产生的重力压降较小，此时采用阻力系数法尤其适用。它忽略了气液滑脱对混合物密度的影响，将流型特征、滑脱效应、摩阻规律均反映于阻力系数中。于是混合物密度采用无滑脱密度计算：

式中ρg、ρL分别为气相、液相密度，kg／m3；λL为无滑脱持液率；vsL为液相表观流速，m／s。

两相阻力系数需要同时考虑气、液两相物性参数、流动参数和质量含量的影响，可以利用无因次两相雷诺数来描述［14］，其定义为：

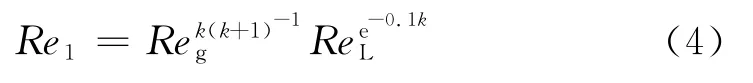
气相折算雷诺数为：

液相折算雷诺数为：

式中k为气液质量比；vsg为气相表观流速，m／s；μg、μL分别为气相、液相黏度，Pa·s。

由式（4）可知，当气、液产量不为0时，两相雷诺数反映了气、液两相的综合影响，当产液量接近0时，两相雷诺数接近气相雷诺数；当产气量接近0时，两相雷诺数接近液相雷诺数。

2 阻力系数图版回归

2．1 实测数据反算阻力系数

搜集到四川盆地南部及鄂尔多斯盆地66口宽气液比范围的产水气井的实测压降数据，来作为拟合阻力系数图版的基础资料。其数据范围为：气液比480～344 360m3／m3，油压4．39～18．69MPa，井底压力10．59～39．19MPa，产气量（0．81～20．52）×104m3／d，产液量0．1～51m3／d，油管内径50．7～76mm，井深2 330～3 260m，产出水相对密度1．01～1．09，气体相对密度0．57～0．83。由以上数据反算每个测点的阻力系数步骤如下：

1）每个测点的压力、温度和压力梯度已知，计算每个测点的基本物性参数，进而得到ρg、ρL、vm、vsL等参数。

2）由式（2）、式（3）反算混合物密度（ρm）。

3）由式（1）反算每个测试点的阻力系数（fm）。

2．2 新阻力系数图版

将所得的66个阻力系数值与式（4）定义的两相雷诺数共同绘入对数坐标图1中。由图1可知，两相雷诺数分布在1．32×105～1．30×108、阻力系数分布在0．005 8～21．02。该阻力系数不仅考虑了摩阻的影响，还考虑了流型、气液滑脱的影响，因此其值普遍大于传统Moody图版［17］中单相气体摩阻系数。由图1还发现，反算数据点较分散，函数关系不明显，为了实现阻力系数图版的最佳拟合，有必要对两相雷诺数进行修正。

图1 阻力系数与两相雷诺数Re1关系图

通过多次回归试算后，发现对两相雷诺数进行如下修正，可以将阻力系数回归为一条单一曲线。即

上式中的α、β、γ是两相雷诺数的修正系数，反映了真实气井条件下气液质量比对两相雷诺数的影响，会影响到图1中的曲线形态，当α＝3．55、β＝－0．16、γ＝－0．012时拟合程度最佳。图2中曲线即为新的阻力系数图版，其拟合方程为：

图2 新的阻力系数图版

2．3 压力梯度计算步骤

应用新阻力系数图版（图2）计算气井压力梯度简单方便，其具体步骤为：

1）由式（5）、（6）计算Reg、ReL。

2）由Reg、ReL和气液质量比（k），按式（7）计算修正的两相雷诺数（Re2）。

3）由图2或式（8）得到阻力系数（fm），由式（2）、式（3）计算混合物密度（ρm）。

4）由式（1）确定压力梯度。

计算中涉及气体或液体密度、黏度等物性参数按本文参考文献［17］中推荐公式计算。

3 模型评价

选用公开文献 Texas Railroad Commission 50口气井测压数据［18］对新的阻力系数法进行评价。其中气井数据范围如下：气液比150～138 923m3／m3，油压5．56～65．09MPa，井底压力10．94～81．98MPa，产气量1．3×104～70．5×104m3／d，产液量0～347．9 m3／d，油管内径40．9～100．5mm，井深2 206～6 539 m，油相对密度0．73～0．82，气体相对密度0．59～0．88。由于缺少水分析数据，假定地层水的相对密度为1．02。图3即为新的阻力系数法计算井底压力与实测井底压力对比图。

图3 井底压力计算值与实测值对比图

由图3可知，新的阻力系数法在不同的气液比范围内（GLR＜2 000、2 000＜GLR＜10 000、GLR＞10 000）均具有较低的误差和离散程度，流压平均相对误差仅为2．48%，流压平均绝对误差仅为5．37%，说明该方法能够满足高气液比气井压降计算需要。

4 结论

1）提出了一个适用于气井压降计算的阻力系数图版，适用的气液比范围在480～344 360m3／m3，其中回归数据取自川南及鄂尔多斯地区66口产水气井测压数据。

2）新图版的阻力系数是关于修正的无因次两相雷诺数的函数。因此不受变量量纲的限制，应用范围更广。

3）利用公开文献50口气井的压降测试数据评价表明，新图版能够满足工程需要且计算简单方便。

［1］常志强，肖香姣，朱忠谦，等．高温高压气井、凝析气井井筒及近井地带的压力变化规律［J］．天然气工业，2012，32（10）：47－51．CHANG Zhiqiang，XIAO Xiangjiao，ZHU Zhongqian，et al．Pressure change law at the wellbore and well－adjacent zone of a HTHP or condensate gas well［J］．Natural Gas Industry，2012，32（10）：47－51．

［2］杨焦生，王一兵，王宪花．煤层气井井底流压分析及计算［J］．天然气工业，2010，30（2）：66－68．YANG Jiaosheng，WANG Yibing，WANG Xianhua．Analysis and computation of flowing bottom－hole pressure in coalbed methane wells［J］．Natural Gas Industry，2010，30（2）：66－68．

［3］朱瑞，吕涛，胡勇，等．裂缝性气水两相地层井筒组合数值模拟［J］．西南石油学院学报，2002，24（5）：37－39．ZHU Rui，LYU Tao，HU Yong，et al．A combined numerical simulation for transient two－phase flow of gas and water in the wellbore／reservoir with fracture［J］．Journal of Southwest Petroleum Institute，2002，24（5）：37－39．

［4］GOMEZ L E，SHOHAM O，SCHMIDT Z，et al．Unified mechanistic model for steady－state two－phase flow：Horizontal to vertical upward flow［J］．SPE Journal，2000，5（3）：339－350．

［5］KAYA A S，SARICA C，BRILLl J P．Mechanistic modeling of two－phase flow in deviated wells［J］．SPE Production＆ Facilities，2001，16（3）：156－165．

［6］SHOHAM O．Mechanistic modeling of gas－liquid twophase flow in pipes［M］．New York：Society of Petroleum Engineers，2006．

［7］REINICKE K M，REMER R J，HUENI G．Comparison of measured and predicted pressure drops in tubing for highwater－cut gas wells［J］．SPE Production Engineering，1987，2（3）：165－177．

［8］LI Y C，DU Z M．A new numerical model for two－phase flow in liquid－cut gas wells［C］∥paper 35612－MS presented at the SPE Gas Technology Symposium，28April －1 May 1996，Calgary，Alberta，Canada．New York：SPE，1996．

［9］HASAN A R，KABIR C S．A simple model for annular two－phase flow in wellbores［C］∥paper 95523－MS presented at the SPE Annual Technical Conference and Exhibi－tion，9－12October 2005，Dallas，Texas，USA．New York：SPE 2005．

［10］陈家琅，陈涛平．石油气液两相管流［M］．北京：石油工业出版社，2010．CHEN Jialang，CHEN Taoping．Gas－liquid two－phase pipe flow in petroleum industry［M］．Beijing：Petroleum Industry Press，2010．

［11］POETTMANN F H，CARPENTER P G．The multiphase flow of gas，oil，and water through vertical flow strings with application to the design of gas－lift installations［J］．Drilling and Production Practice，1952，14（4）：257－317．

［12］BAXENDELL P B，THOMAS R．The calculation of pressure gradients in high－rate flowing wells［J］．Journal of Petroleum Technology，1961，13（10）：1023－1028．

［13］FANCHER G H Jr，BROWN K E．Prediction of pressure gradients for multiphase flow in tubing［J］．SPE Journal，1963，3（1）：59－69．

［14］TEK M R．Multiphase flow of water，oil and natural gas through vertical flow strings［J］．Journal of Petroleum Technology，1961，13（10）：1029－1036．

［15］陈家琅．油、气、水混合物垂直管流的压降计算——阻力系数法［J］．石油勘探与开发，1979，6（6）：57－64．CHEN Jialang．Calculation of pressure drop for oil／gas／water mixture flow in vertical tubing－friction factor method［J］．Petroleum Exploration and Development，1979，6（6）：57－64．

［16］郭冀义，韩玉堂，齐占奎．气井油管流动计算动能项的取舍［J］．天然气工业，2007，27（3）：80－82．GUO Jiyi，HAN Yutang，QI Zhankui．Treatment of the kinetic energy term for calculation of flowing performance in gas well tubings［J］．Natural Gas Industry，2007，27（3）：80－82．

［17］李士伦．天然气工程［M］．2版．北京：石油工业出版社，2008．LI Shilun．Natural gas engineering［M］．2nded．Beijing：Petroleum Industry Press，2008．

［18］PEFFER J W，MILLER M A，HILL A D．An improved method for calculating bottomhole pressures in flowing gas wells with liquid present［J］．SPE Production Engineering，1988，3（4）：643－655．