广域继电保护中一种故障判定算法

李运坤，江登笠，周文越

(1.德阳电业局检修公司，四川 德阳 618000;2.四川大学电气信息学院，四川 成都 610065)

0 引言

传统继电保护都是采用离线整定以获得保护定值，但电力系统运行方式太多且变化频繁，因此无法保证定值的灵敏性和选择性随时都满足要求。近几年的大面积停电表明，当发生大范围潮流转移时，传统保护难以区分线路内部故障和过负荷［1］。为提高继电保护的性能，提出了广域继电保护的概念，即利用电力系统中不同位置的广域测量信息来实现继电保护的功能。在现有的高压系统中，主保护通常是基于纵联差动原理进行动作判定的，能不受电网运行状态的影响而快速确定故障位置。因此广域继电保护一般用于后备保护。

近年来，人们对广域继电保护展开了广泛的研究。在系统结构方面，文献［2－3］根据图论中的相关知识划分保护区域，文献［4］将多Agent 引入广域继电保护的体系结构。在保护算法方面，文献［4－6］根据底层终端的智能电子设备(IED)的方向信息实现故障判定，文献［7］利用电压测量信息组成故障判据。为提高保护的容错性能，文献［8－10］融合电网多点信息实现故障元件识别。

这里对广域继电保护的算法进行了研究。在混合式广域继电保护系统模型的基础上，利用Petri 网得到元件/IED 关联矩阵，矩阵中的每个元素表明相应元件与IED 的关联程度，然后将IED 的方向信息作为主判据，主保护和距离I 段的动作信息作为辅助判据，识别故障元件。需要说明的是，这里所指的元件都为电网的一次设备。

1 广域继电保护系统结构

广域继电保护的系统结构可分为3种:集中式、分布式和混合式［11］。

集中式结构从整个大电网采集数据，控制中心对数据进行整理分析并决策，然后将处理信息发送给各个IED 执行决策。分布式结构将数据的分析和决策放在每个IED 上。

综合集中式结构和分布式结构的优点，提出了混合式系统结构。这种结构对整个电网进行分区处理，每个局域网内有单独的控制决策中心进行数据处理以及决策，并与相邻局域网的控制中心进行信息交换。就目前看来混合式系统结构应该是广域继电保护系统的最佳结构。从整体上看，混合式系统结构与分布式结构相似，每个局域网等同于一个IED，相邻局域网之间进行必要的信息交换，但主要信息在局域网内部传输，因此减少了不必要的信息通信。从局域网层面来看，混合式系统结构又与集中式结构相似，在局域网内部，决策中心负责全部的信息处理，避免了单个IED 获取信息过于单一的缺点。再则，考虑到系统升级后，单个IED 功能更加完善或者决策中心信息处理能力大幅提高，混合式结构很容易过度到其他两种结构。图1 为混合式系统结构示意图。

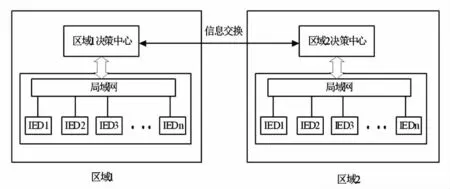
图1 混合式系统结构示意图

这里的故障判定算法是建立在混合式系统结构的基础上。所分析的电网均为单个局域网。对于广域继电保护的保护区域划分方法，可参见相关文献，这里不做详细讨论。

2 元件/IED 关联矩阵

如图2 所示的电网，被保护的元件为母线B1～B5，线路L1～L5，每个保护上都安装一个IED，可测量该位置短路电流方向，读取所安装保护的动作信息。

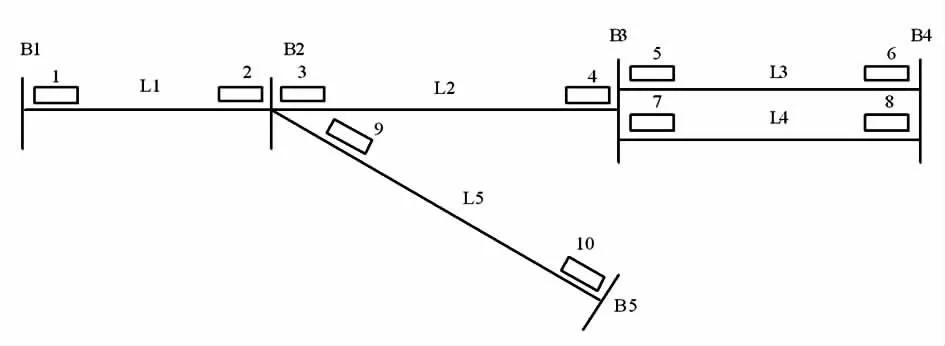
图2 某电网接线图

受与故障元件距离、灵敏度等因素影响，电网内的IED 对于故障的反映程度有所不同。对于某一个电力元件而言，其自身保护装置中IED 的故障信息无疑是最准确的，其次相邻元件中的IED 也能从某种程度上反映故障元件的特征。因此，希望广域继电保护系统的决策中心在进行故障识别时，能够识别IED 与电力元件的这种关系，即对于特定的故障元件，决策中心应当按照IED 故障信息的价值对IED 加以区分。因此，引入了元件/IED 关联矩阵的概念。

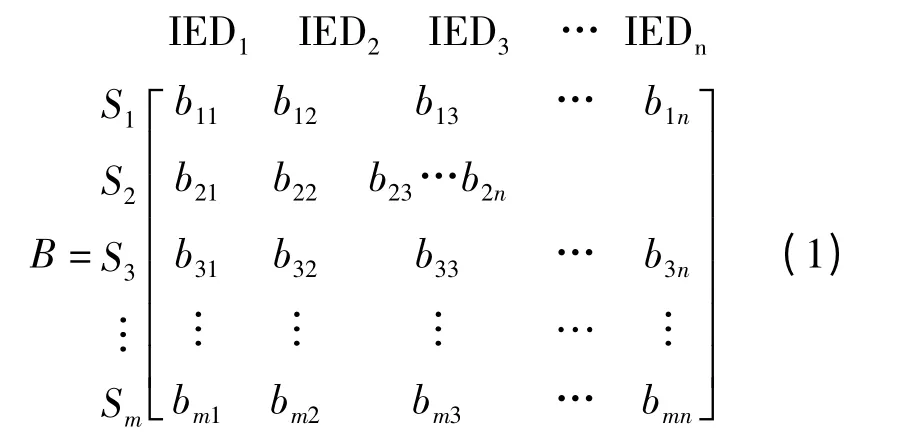
如式(1)所示，m×n 维矩阵B 为一个元件/IED矩阵。矩阵的每一行代表一个被保护元件，每一列代表一个IED，矩阵的元素量化了元件与IED 的关联程度。下面将详细阐述基于Petri 网推导元件/IED 矩阵的方法。

2.1 Petri 网的基本原理

Petri 网是一种可以用图形表示的组合模型，又是严格定义的数学对象，可以很方便地用于静态结构分析和动态的行为分析。图3 为Petri 网的典型结构，圆圈表示库所，方框表示变迁，箭头表示有向弧，黑点表示令牌。Petri 网的基本规则为:有向弧必须是有方向的;两个库所或变迁之间不允许有弧;位置节点可以拥有任意数量的令牌。

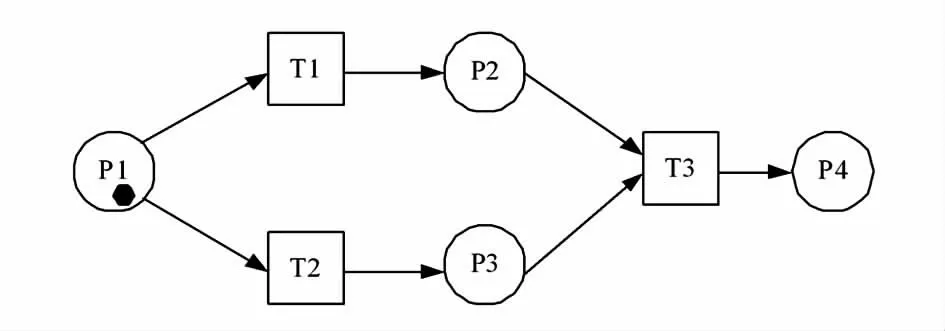
图3 Petri 网典型结构

如果一个变迁的每个输入库所都拥有令牌，该变迁即为被激活。一个变迁被允许时，变迁将发生，输入库所的令牌被消耗，同时为输出库所产生令牌。

2.2 元件/IED 矩阵推导过程

以图2 所示电网为例说明基于Petri 网的元件/IED 矩阵推导方法。电网中的IED 等同于库所，被保护元件等同于变迁，元件与IED 间的功率流动等同于有向弧，方向为由母线到LED，由LED 到线路。于是图2 所示电网可等同于图4 所示Petri 网。以推导元件/IED 矩阵中L2 所在行为例，假设L2 故障，放置一个带令牌的库所指向L2 所在变迁。

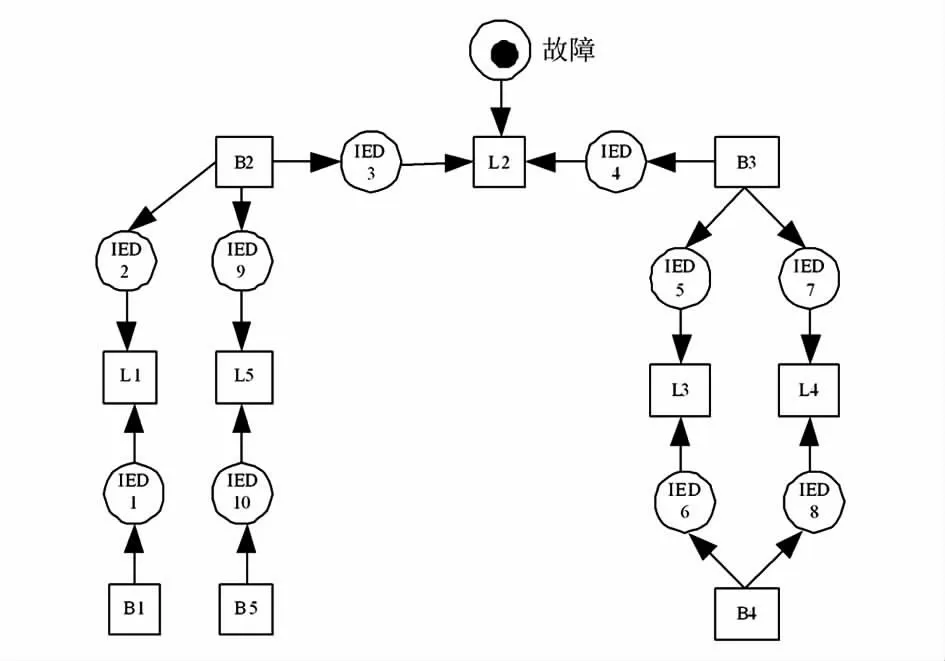
图4 电网的Petri 网模型

元件/IED 矩阵的求解过程就是令牌在各个库所的转移过程，也就是令牌从故障库所一步步向各个IED 库所的转移过程，令牌的每一次转移，都是从一个库所转移到离它最近的库所，得到令牌的库所将令牌保存并沿着有向弧继续向其他库所转移令牌，一直重复此过程，直到Petri 网中所有的库所都接受到令牌。

定义3 个矩阵U、M、C。U 与网络结构相关，保持不变。M、C 都为动态矩阵，随着令牌的转移不停变化。

U 为变迁/库所关联矩阵，表明变迁与库所的关系。矩阵的每一列代表一个库所，每一行代表一个变迁。当变迁是库所的输出时uij=1，当变迁是库所的输入时uij=－1。图2 所示电网的U 为式(2)所示矩阵，其中行按IED1～IED10 排列，列按L1～L5、B1～B5 排列。

M 为令牌位置矩阵，Mi表示第i次推导的M 矩阵，表明令牌在Petri 网中的分布。对图2 所示电网，M 的列按IED1～IED10 排列，这里未考虑故障库所。

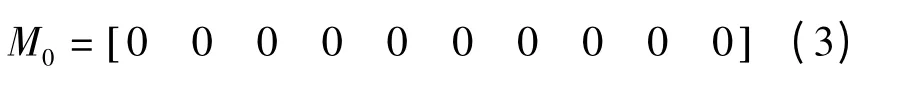
C 为变迁激活矩阵，Ci表示第i次推导的C 矩阵，表明Petri 网中被激活的变迁。如果令牌的转移是从线路到IED，即与规定的正方向相反，则在C 中的相应位置取－1，反之如果令牌的转移是按规定的正方向转移则在C 中的相应位置取1。C 可由M·UT计算得到。由于未考虑故障库所，M0为全零矩阵，因此不能用M0·UT得到C1。对图2 所示电网，C 的列按L1～L5、B1～B5 排列。从图4 可以看出，变迁L2 被激活。

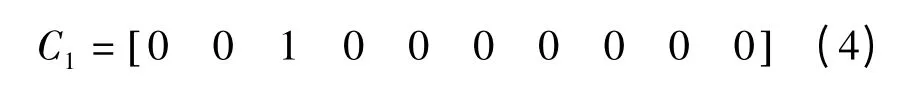
令牌在Petri 网中的传播过程可用下面两个式子表示。

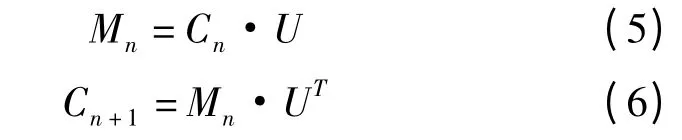
按式(5)、式(6)进行迭代操作，直到网络中每个库所至少有一个令牌，即矩阵M 中无零元素。

对图4 所示Petri 网进行上述操作，经过三次迭代，可得

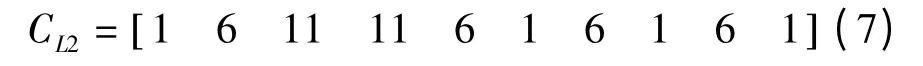
ML2为最终L2 对应的令牌位置矩阵。从矩阵ML2可以看出，IED3、IED4 所在列数值最大，IED2、IED5、IED7、IED9 其次，IED1、IED6、IED6、IED10 最小。这些值表明了L2 与各IED 的相关程度。

当L2 发生短路故障时，IED1、IED3、IED4、IED6、IED8、IED10 处的方向元件判定为负方向，IED2、IED5、IED7、IED9 处的方向元件判定为正方向。用矩阵I 表示这种关系，I 的列按IED1～IED10排列。

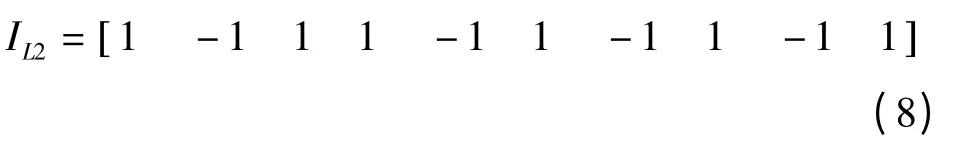
IL2表示L2 与各IED 的方向关系，将IL2与ML2点乘，便可将方向信息加入元件与IED 的相关程度中。修改ML2矩阵为

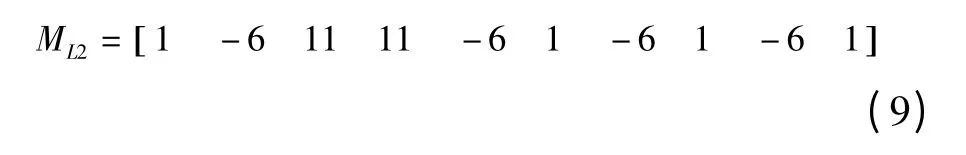
对电网中的每个元件，按上述方法进行推导时，U 都是一样的，需要改变的是C1和I。需注意的是，为保持每个元件的M 矩阵中元素的符号统一，在推导母线的M 矩阵时，C1中的元素取为负。将所有M矩阵组合成一个矩阵如下。

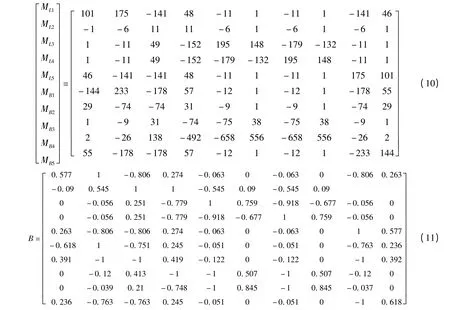
可以看出，不同元件M 矩阵各元素的值相差较大，由于只需要反应元件与IED 之间相对关联程度，因此为方便比较，将矩阵中的各元素除以元素所在行最大的绝对值，最后得到的矩阵便为元件/IED关联矩阵。矩阵中的某些元素可能非常小，这表明对应的元件与IED 关联程度相当低，于是可直接忽略，将该元素置零。最后得到的矩阵即为元件/IED关联矩阵B。

借用Petri 网络的基本概念和原理，对元件/IED矩阵的元素取值进行推导，过程直观简便，只需要简单的矩阵运算，便可从数学的角度量化关联矩阵的元素值，从而达到对元件与IED 之间关联矩阵赋值的目的。相对于其他算法，Petri 网络不需要在庞大的解空间内寻求最优解，从而降低了运算难度。当电网结构发生变化时只需修改矩阵U 中的相关元素即可。可以看出，基于Petri 网推导元件/IED 关联矩阵的过程即是不断对电网中IED 进行赋值，而与元件关联越紧密的IED 被赋值的次数也就越多，因此最后得到的元件/IED 矩阵反映了元件与IED的关联程度。

3 故障判定算法

将方向元件的动作信息作为故障判定的主判据。而主保护和距离Ⅰ段误动率很低，因此为充分利用冗余信息，将主保护和距离Ⅰ段的动作信息作为故障判定的辅助判据。

方向元件可能的动作情况为

当保护动作时，经过一段延时后，局域网的决策中心在一定的时间范围内收集所有IED 方向元件以及主保护和距离I 段的动作信息，并按照式(12)、式(13)、式(14)进行赋值。分别用矩阵F、Z、L 表示电网中方向元件、主保护和距离I 段的动作信息。

n 为电网中IED 的数量。上面3 个矩阵的每1列代表1 个相应位置保护的动作信息，排列顺序与元件/IED 矩阵列的排列顺序一致。

在得到电网的元件/IED 关联矩阵和式(15)、式(16)、式(17)3 个矩阵后，便可用式(18)计算故障判定值。

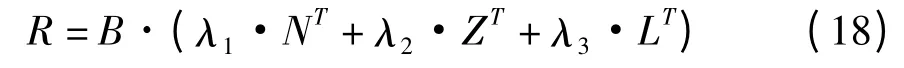
式中，λ1、λ2、λ3为权重因子，考虑到方向信息为主判据，主保护和距离Ⅰ段的动作信息为辅助判据，λ1应大于λ2、λ3。R 代表系统中保护范围内所有元件的故障判定值ri组成的列相量如下。

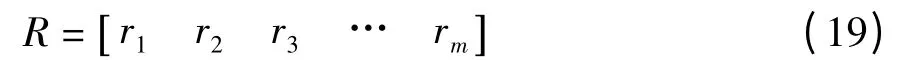
式中，m 为电网中元件的数量。式(19)就是将每个IED 动作值、主保护和距离Ⅰ段动作值与对应IED与每个元件的关联度相乘，然后将3 个值相加。由于元件/IED 矩阵已进行过归一化处理，因此式(20)所得向量R 中的元素定量表示了元件故障概率的相对大小。

元件的故障判据为

式中，riset为预先设定的故障阈值。电网中的每个元件都有自己的故障阈值，应该根据电网的拓扑结构选择每个元件合适的故障阈值。这里从两方面考虑元件的故障阈值。首先，考虑到故障定位的准确性与可靠性，阈值应适当取高;其次，当通信故障或IED 灵敏度不够时，可能会造成电网内某些IED 不动作或误动，此时因考虑较低的阈值。因此，在计算元件阈值时，应假设该元件故障，在电网内所有IED都正确动作时确定一个阈值，然后以N－1 切换的方式考虑单个IED 故障时，再考虑一定的裕度便可确定最终的元件故障阈值。

4 算例分析

以图2 所示电网为例说明所提出的广域继电保护故障判定算法。λ1、λ2、λ3分别为1、0.5、0.5。电网的元件/IED 矩阵为式(11)所示矩阵。假设线路2 中点处发生故障，保护动作正确、方向元件2 误动、拒动。按式(16)计算各个元件的故障判定值，最终的判定结果见表1。

从表1 可以看出，故障线路的故障判定值要明显高于其他非故障线路的故障判定值，主要原因在于，在用方向信息进行故障判定时，在非故障线路中负方向元件动作后起到一定的负反馈作用，从而部分抵消了非故障线路的正方向元件动作后的故障计算值，而在故障线路中负方向元件则起到了正反馈作用，使判定值增大。根据这种特征，再加以主保护和距离I 段动作信息的辅助判据，决策中心就能区分故障元件与非故障元件，且具有较强的容错性。因此，只要阈值设定合理，即使某个保护误动或拒动，决策中心仍能正确判定故障。

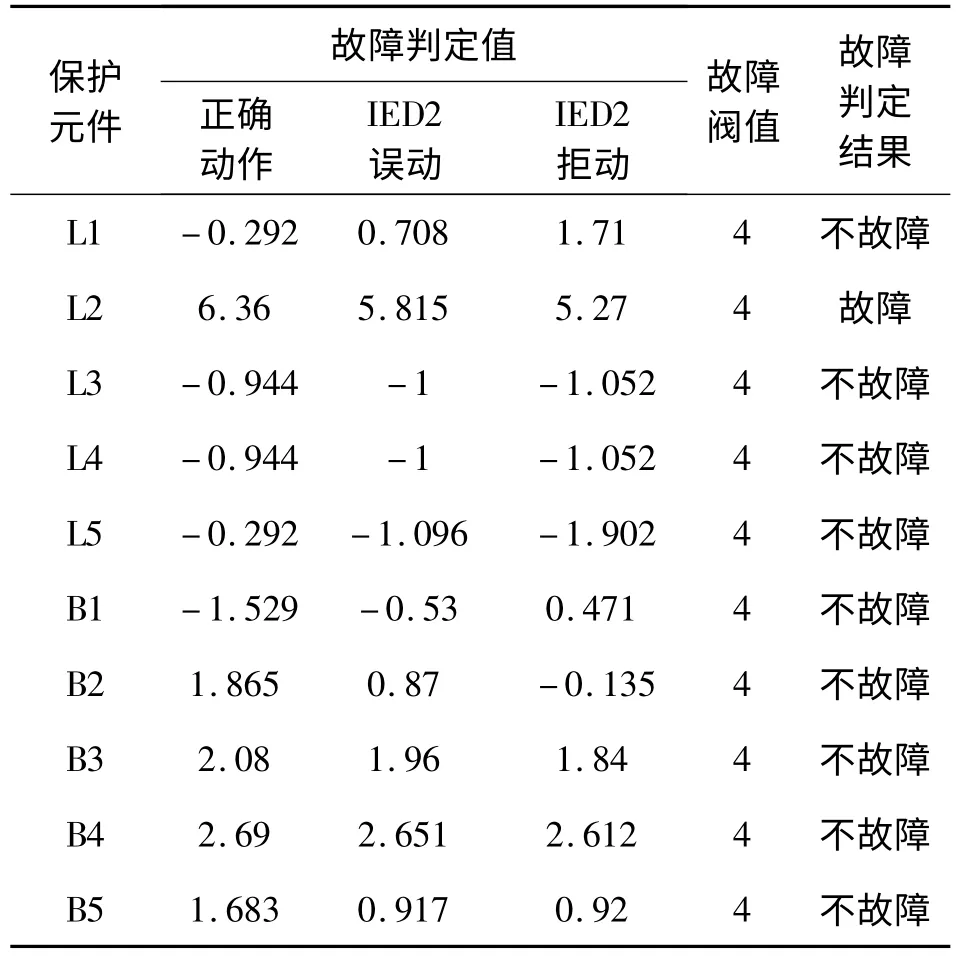
表1 故障判定结果

5 结语

在混合式广域继电保护系统结构的基础上，基于Petri 网推导出表示电网一次设备与IED 关系的元件/IED 关联矩阵。推导过程简单，当网络结构发生改变时，易于更新。故障发生后，将IED 的方向信息作为主判据，主保护和距离Ⅰ段的动作信息作为辅助判据，并借助元件/IED 关联矩阵进行故障判定。通过算例分析表明，该算法能很好的分辨出故障元件与非故障元件，并具有较强的容错性。

［1］杨春生，周步祥，林楠，等.广域保护研究现状及展望［J］.电力系统保护与控制，2010，38(9):147－150.

［2］苏盛，K.K.Li，W.L.Chan，等.广域电流差动保护区划分专家系统［J］.电网技术，2005，29(3):55－63.

［3］李振兴，尹项根，张哲，等.有限广域继电保护系统的分区原则与实现方法［J］.电力系统自动化，2005，29(3):55－63.

［4］李振兴，尹项根，张哲，等.基于多Agent 的广域保护系统体系研究［J］.电力系统保护与控制，2012，40(4):71－75

［5］丛伟，潘贞存，赵建国.基于纵联比较原理的广域继电保护算法研究［J］.中国电机工程学报，2006，26(21):8－14

［6］田聪聪，文明浩.具有高信息冗余的广域后备保护系统［J］.电网技术，2011，35(10):214－219

［7］杨增力，石东源，段献忠.基于方向比较原理的广域继电保护系统［J］.中国电机工程学报，2008，28(22):97－93

［8］汪华，张哲，尹项根，等.基于故障电压分布的广域后备保护算法［J］.电力系统自动化，2011，35(7):48－52

［9］汪旸，尹项根，赵逸君.基于遗传算法的区域电网智能保护［J］.电力系统自动化，2008，32(17):40－44

［10］汪旸，尹项根，张哲，等.基于遗传信息融合技术的广域继电保护［J］.电工技术学报，2010，25(8):174－179

［11］尹项根，李振兴，刘颖彤，等.广域继电保护及其故障元件判别问题的探讨［J］.电力系统保护与控制，2012，40(5):1－9