考虑电量分布及行驶里程的高速公路充电站规划
葛少云,冯 亮,刘 洪,王 龙
(天津大学 智能电网教育部重点实验室,天津 300072)
0 引言
目前,环境和能源问题日益突出,节能与环保也成为世界各国所追求的发展模式[1-2]。高污染和高耗能的缺点使得传统燃油汽车的发展受到了极大的限制,而电动汽车的出现却给未来的汽车行业提供了一个长远发展的解决方案[3-4]。
电动汽车的相关技术已成为国内外众多学者的研究热点,而作为电动汽车推广应用的前提和基础,充电设施的规划和建设也逐步引起人们的重视[5]。文献[6-7]分析了大量电动汽车的充电行为对电网所带来的影响。文献[8-9]研究了对电动汽车充电行为的优化调度与控制问题。文献[10-11]研究了电动汽车的充电需求和负荷特性,并提出了相应的计算方法。文献[12]介绍了我国电动汽车充电站的发展现状,提出了影响电动汽车充电站规划的因素和所需遵循的原则。文献[13]以居民负荷的分布情况模拟电动汽车的数量,以投运至目标年最大化充电站运营收益作为目标来进行充电站的选址规划。文献[14]根据电动公交客车的运行机制和动力电池的功率变化特性构建了电动公交客车充电站的容量需求预测模型,建立了定功率工况下的充电机制。文献[15]将电动汽车充电设施规划划分为示范阶段、公益阶段和商业运营阶段,并根据每个阶段的特点提出了充电方式的选择优化模型以及充电设施规划的原则、流程和模型。文献[16]提出了电动汽车充电站规划的两阶段模型,第一阶段利用聚类分析法将区域的路况信息转化为充电需求集群,第二阶段在考虑一定的约束和资金因素等条件下,利用优化算法进行电动汽车充电站的优化选址。文献[17]运用动态交通网络思想建立了基于硬时间窗约束下的充电站布局及确定最佳规模的多目标优化模型,并提出了求解该模型的两阶段启发式算法。文献[18]以包含充电站配电网投资与运行成本最小为目标,建立了考虑充电站布局优化的配电网规划模型。文献[19]对具有反向放电能力的电动汽车充电站的入网方案进行了分析,总结了各种典型方案的优缺点及其适用范围。
目前已发表的文献主要关注于城市区域内电动汽车充电站的规划建设情况,而对于电动汽车的长距离行驶及高速公路充电站的建设情况则较少涉及。因此,本文针对高速公路的车流情况和充电需求特点构建了高速公路充电站的规划模型。主要研究在考虑电动汽车电量分布和行驶里程的情况下,充电站的布局和容量配置问题,并通过算例进行了验证。
1 选址模型
由于在高速公路上,汽车是单向行驶的,不能掉头,如果需要充电只能到前面最近的充电站进行充电,并且2个方向的车流互不影响,所以本文在构建高速公路的充电站选址模型时,只考虑了一个方向的车流情况,对于另一方向可采用相同的方法进行规划和布局。
假设某一高速路段如图1所示,各路口位置用A1、A2、…、An、An+1表示,从各路口进入该高速公路的汽车数量用 Q1、Q2、…、Qn、Qn+1表示。

图1 某高速路段示意图Fig.1 Schematic diagram of a highway
若该高速路段欲建m座充电站,则这m座充电站站址的选择应以充电站收益最大化为目标,即到这m座充电站充电的电动汽车数量最大。所以,本文以高速路段中到充电站充电的电动汽车的数量期望值最大化为目标来进行高速公路充电站的站址选择和布局。目标函数可表示为:
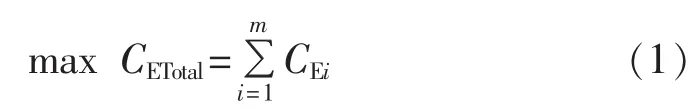
其中,CETotal为高速路段中m座充电站所服务的电动汽车总的期望值;CEi为第i座充电站所服务的电动汽车的期望值。
若第i座充电站的站址li位于路口Aj和Aj+1之间,则:
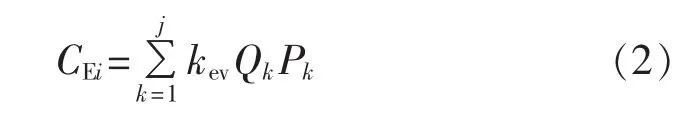
其中,j=1,2,…,n;kev为电动汽车的比例;Qk为由 k路口进入该高速路段的汽车数量;Pk为由k路口进入该高速路段的电动汽车行驶到li位置时需要充电的概率。
用Lmax表示电动汽车的最大行驶里程,x表示电动汽车现存电量比例,α表示电量的警戒值,则需要充电的电动汽车即为电量处于0≤x≤α的电动汽车。若Qk>0(表示k路口有Qk辆汽车驶入该高速公路路段),则:

若从外界驶入该高速路段的电动汽车的电量服从函数 F(x)的概率分布,则式(3)又可表示为:
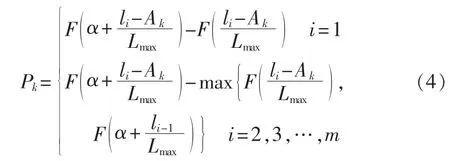
若Qk<0(表示k路口有Qk辆汽车驶出该高速路段),则:

其中,Ek为行驶到k路口时需要充电的电动汽车期望值,计算方法同CEi。
2 定容模型
电动汽车充电站对电动汽车的充电服务是随机的,因此可用排队论(或称随机服务系统理论)来对充电站的充电机配置进行优化。
2.1 排队论的基本原理及指标
排队论,是通过对服务对象到来及服务时间的统计研究,得出这些数量指标(等待时间、排队长度、服务强度等)的统计规律,然后根据这些规律来改进服务系统的结构或重新组织被服务对象,使得服务系统既能满足服务对象的需要,又能使机构的费用最经济或某些指标最优[20]。
电动汽车到达充电站接受服务是相互独立的,满足平稳性、无后效性及普通性的特点。因此可以用参数为λ的泊松流来表示电动汽车到达充电站的规律,则电动汽车接受充电服务的时间服从参数为μ的负指数分布。若充电站有c台充电机,则整个充电站的平均服务率为 cμ(n>c)或 nμ(n≤c),ρ=λ/(cμ)称为充电站的服务强度,该充电站属于标准的M/M/C/∞/∞排队系统模型,则系统状态转移关系图如图2所示。

图2 充电站排队系统状态转移关系图Fig.2 State transition diagram of charging station queuing system
排队系统稳态的平衡方程[21]为:
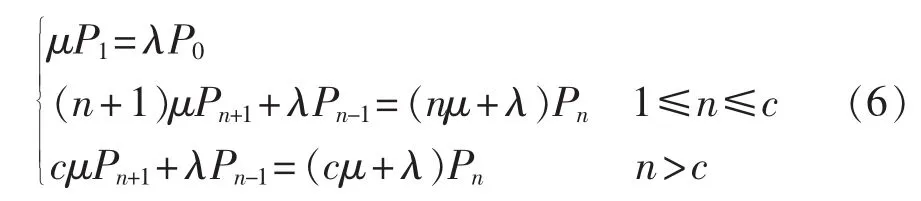
其中,Pn为有n辆电动汽车接受充电服务的概率,且。
利用递推法求解式(6)所示的差分方程,可得电动汽车充电服务的概率为:

由此可得充电站排队服务系统的运行指标如下。
充电站的平均排队长度Lq为:

充电站的平均队长Ls为:

顾客在队列中的平均等待时间Wq为:

顾客在充电站的平均逗留时间Ws为:

充电机的空闲比例I0为:
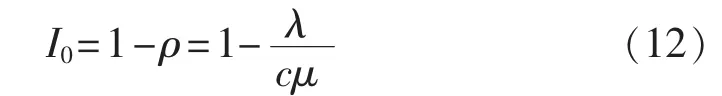
2.2 充电机的优化配置
对于充电站而言,若充电机配置较多,则充电站的服务成本会增加,服务水平会有所提高,顾客在充电站中由于等待所花费的成本会降低;相反,若充电机配置较少,充电站的服务成本会减少,服务水平会降低,而顾客在充电站中由于等待所花费的成本会增加。所以,本文兼顾了充电站与顾客双方的利益,以充电站的服务成本和顾客的等待费用之和最小为目标来优化配置充电站的充电机台数。
在稳态的情况下,设单位时间内每个充电机的成本费用是cs,每个顾客在充电站停留单位时间的费用为cw,则单位时间内的费用(服务成本和等待费用之和)的期望值为:

其中,Ls是 c的函数,因此,系统的总费用 z=z(c)是关于c的函数,记c*为充电机的最优配置台数,则z(c*)即为最小费用,由于 c 只能取整数,z(c)是离散函数,所以采用边际分析法求解,则有:
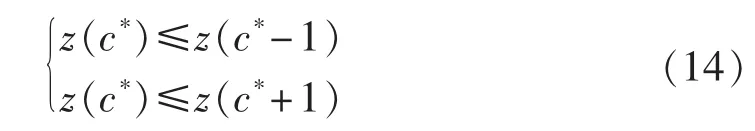
将式(13)代入式(14),可得:

化简整理,可得:

由式(16)即可求得充电站的最优充电机配置台数c*。
3 算例分析
3.1 基础数据
假设某一高速路段如图3所示。该路段各路口位置可表示为 A=[0,24,54,104,120](单位为km),高速路段及各路口典型日的车流量可表示为Q=[14808,1398,570,-2748,-14028](单位为辆),到规划目标年,预计电动汽车所占车辆比例为15%,最大行驶里程为120 km,电量警戒值为30%。

图3 规划路段示意图Fig.3 Schematic diagram of trunk road
假设进入该路段的电动汽车的电量分布满足参数为τ=0.5、σ=0.204的正态分布,则其概率密度函数为:
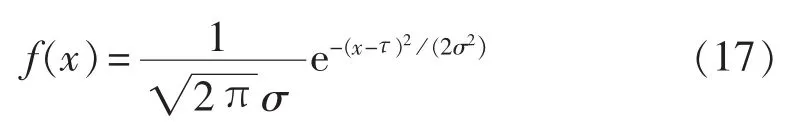
3.2 充电站数量预估
设驶入高速路段的电动汽车电池中的电量比例为x(0≤x≤1),且电动汽车驶入与驶出的路口分别为 Ai、Aj(i=1,2,3;j=4,5),则电动汽车在该高速路段所消耗的电量在电池中的比例为:

若电动汽车在该高速路段不需要充电,则需满足:

若电动汽车在该高速路段只充电1次,则需满足:

化简,可得:

若电动汽车在该高速路段需充电2次,则需满足:

由该高速路段的长度、电动汽车的最大行驶里程及电量警戒值分析可知,在该高速路段电动汽车最多需要充电2次。
若该高速路段中的电动汽车所需要的充电电量总和为S,设充电站的标准容量配置为Sm,则可估算该路段所需建设的充电站数量:

设电动汽车电池的平均容量为50 kW·h,充电站的标准容量配置为20台充电机,则由式(18)—(23)计算可得,该高速路段需建设4座充电站。
3.3 站址选择
按照式(1)—(5)所示方法,并运用遗传算法对路段的充电站站址位置进行优化选择,站址编码采用十进制实数编码方式,适应度函数即为目标函数,求得最优结果如表1所示。

表1 充电站的站址Tab.1 Location of charging stations
由表1可以看出,当4座充电站的位置分别选择19.84 km、39.63 km、72.65 km、104.00 km 处时,电动汽车充电车辆的期望值最大,共为3206辆。充电车辆期望值随行驶里程的变化曲线如图4所示。

图4 充电车辆期望值随行驶里程的变化曲线Fig.4 Curve of charging vehicle expectation vs.driving mileage
在图4中,在l4处充电车辆期望值有一个激增量,这是因为在l1处充电的汽车行驶到l4处时由于行驶消耗其电池内的电量又处于警戒值之内,这部分电动汽车使得l4处的充电车辆期望值产生了一个激增量。
3.4 容量优化配置
根据表1充电汽车期望值可得4个充电站的泊松流参数分别为 λ1=35.38,λ2=30.42,λ3=27.46,λ4=40.33。设充电机的充电时间为30 min,则μ=2。根据充电站的建设费用、运行维护费用、网损费用和运行年限测算每个充电机每小时的服务成本约为cs=5.07元,设用户出行每小时时间价值[22]为cw=17元,利用式(13)和(16)对4个充电站的充电机进行优化配置。4个充电站每小时的费用期望值分别如图5—8所示。
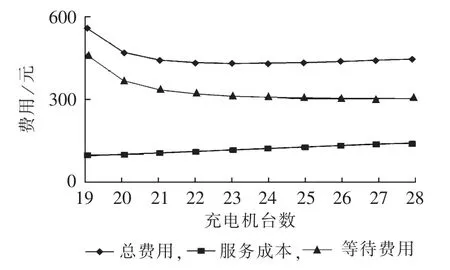
图5 第1座充电站的费用曲线Fig.5 Cost curves of the first station

图6 第2座充电站的费用曲线Fig.6 Cost curves of the second station

图7 第3座充电站的费用曲线Fig.7 Cost curves of the third station

图8 第4座充电站的费用曲线Fig.8 Cost curves of the fourth station
由图5—8可以看出,对于每座充电站都有最优的充电机配置台数使单位时间内充电站的服务成本和顾客等待费用之和最小,4座充电站充电机的最优配置及其对应的每小时费用期望值如表2所示。
根据充电站的配置,利用式(8)—(12)计算3个充电站的运行指标如表3所示。

表2 充电站的最优配置及每小时费用期望值Tab.2 Optimal allocation of charging stations and expected cost per hour

表3 4个充电站的运行指标Tab.3 Operational indicators of four charging stations
由表3可以看出,在4个充电站中,顾客的平均等待时间都不会超过1.2 min,充电站为顾客提供了较好的服务,并且充电站的充电机空闲比例最高只有27.74%,即充电站的充电机利用率达到了72.26%以上。在满足顾客优质服务的基础上,充电站的资源得到了较好的利用。
4 结论与展望
本文在考虑电动汽车电量分布及行驶里程的情况下,提出了一种针对高速路段的充电站选址定容模型。高速路段充电站的布局主要是以路段中到充电站充电的电动汽车的数量期望值最大化为目标。充电站内的充电机台数选择则兼顾了充电站与顾客双方的利益,以充电站的服务成本和顾客的等待费用之和最小为目标来进行优化配置的,同时利用排队论原理分析了充电站的服务水平和运行效率。经过分析可以看出,充电机台数的合理配置,既可以为顾客提供较为优质的服务,也可以使得充电站的资源得到较好的利用。
本文所提出的充电站规划模型主要是基于电量分布和行驶里程等与电动汽车相关的因素来构造的,而对与充电站相连的配电系统相关的因素则暂未考虑,这将在后续的工作中进一步进行研究。

