康铜薄膜压力传感器的有限元分析
李 琦,武文革,李学瑞,范 鹏
LI Qi,WU Wen-ge,LI Xue-rui,FAN Peng
(中北大学 机械工程与自动化学院,太原 030051)
0 引言
合金薄膜压力传感器应变灵敏度较高,具有耐高温和耐腐蚀的特性,能适用于各种恶劣环境下的压力测量[1]。近年来有很多学者致力于各种合金薄膜传感器的特性研究,取得了很多重要的研究成果。例如,胡昌义、高逸群等人研究了铜镍合金的压阻系数[2],发现经退火处理后的铜镍合金性能指标稳定,可以作为各向同性材料对待,具有一定的实用价值。美国威斯康星大学的张绪刚、李晓春等人进行了将微薄膜传感器嵌入Ti6Al4V合金基底的研究[3],设计一出种嵌入式薄膜传感器并对其特性进行了分析。
由于合金薄膜制备工艺较复杂,需要较大的成本投入,若制作出实物后再进行研究会造成不必要的浪费。本文利用ANSYS12.0有限元分析软件对康铜薄膜压阻式传感器进行了静态分析,研究压阻薄膜分布位置、薄膜厚度对传感器输出的影响规律,以此来设计合理的合金薄膜层的尺寸及参数,以期减少研究成本、缩短开发周期。
1 传感器系统及惠斯通电桥设计
应变梁式弹性元件是常用的一种传感器弹性元件结构[4],其中悬臂梁式灵敏度较高,故本文采用悬臂梁结构作为传感器测力系统的弹性元件,悬臂梁结构及康铜薄膜布片方式如图1所示。
传感器悬臂梁结构是由五层材料组成,其中中间一层是弹性元件兼基底,材料为45号钢,基底表面上下两层均为Al2O3绝缘层,在绝缘层表面用物理气相沉积的方法溅射上康铜薄膜应变电阻,设定基底长宽为10mm×2mm,厚度为0.5mm;上下两绝缘层厚度为0.05mm;R1、R2、R3、R14为康铜薄膜应变片,其厚度为0.5μm。将R1、R2、R3、R14由导线连成直流全桥线路[5]。康铜薄膜应变电阻尺寸及其测量电路如图2所示。
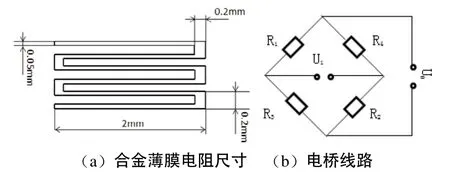
图2 合金薄膜电阻尺寸及电桥线路
传感器用来测竖直方向的压力,连接成全桥电路具有较高的灵敏度,能消除其他方向作用力的相间干扰,且具有温度误差补偿功能。当传感器自由端受如图1的力F作用时,基底产生弹性形变,从而引起薄膜电阻的受力,R1、R2受压力作用,R3、R4受拉力作用,当在电桥输入端端加载电压U0时,输出电压U1为:
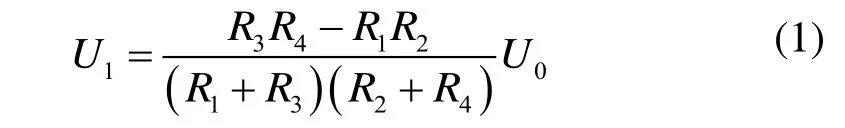
初始时令R1=R2=R3=R4,当传感器受力时各电阻增量分别为,且有,则式(1)可描述为:
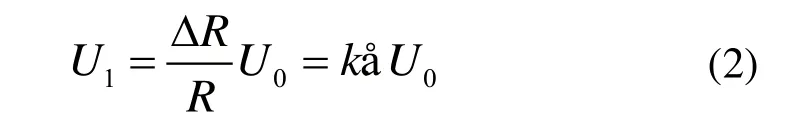
式中,k为电阻灵敏系数,ε为电阻应变,根据胡克定律σ=Eε,可得:

式中,σ为应力,E为弹性模量。由此可知传感器测量电压U1与施加作用力F之间近似成正比。
2 ANSYS建模仿真
压阻分析是一种多场耦合分析,ANSYS软件在多场耦合分析中有着其他有限元软件不可比拟的优势。用ANSYS进行压阻分析时,首先要设置单元类型和材料属性。本文设计的传感器由弹性元件、绝缘层、压阻薄膜和导线组成,其中弹性元件是45号钢,绝缘层是Al2O3,单元类型均采用solid45单元;康铜薄膜设置为solid226单元;导线选为电传导单元solid232,其电阻率设定为0.1×10-10Ωm。所需材料特性如表1所示[2,6]。
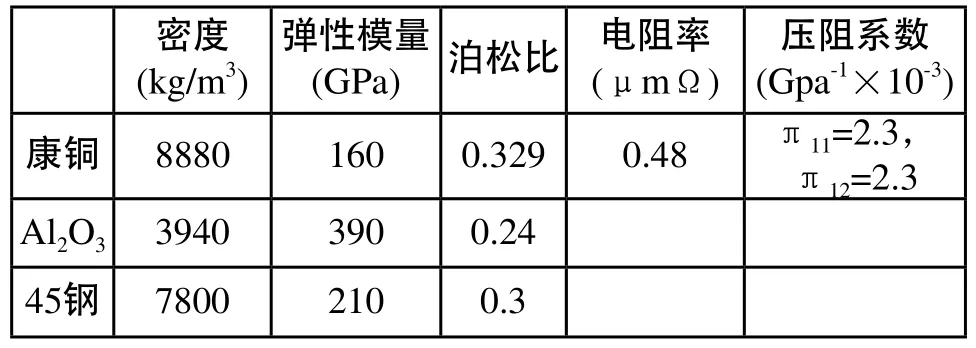
表1 材料特性
其中,康铜材料需要输入的是压阻系数矩阵,由压阻效应原理可知,电阻变化率与压力之间关系为:
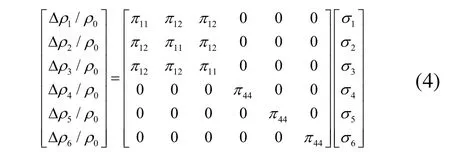
式中,ρ0为初始电阻率,Δρi/ρ0为电阻率变化率,σi为压力,为压阻系数矩阵。经过退火处理后的康铜可以作为各向同性材料[1],因此π44=π11-π12=0。最后所得压阻系数矩阵为:
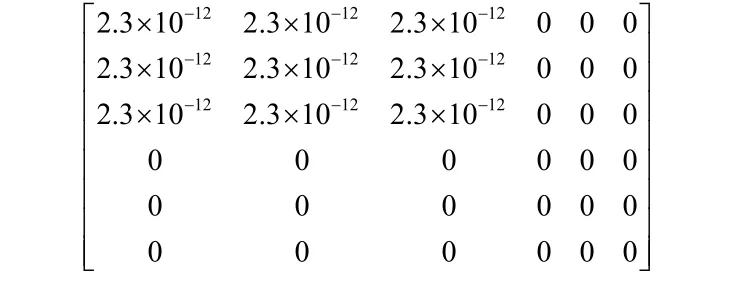
3 结果分析
建立模型图如图3所示,康铜薄膜位置距约束端1mm,设置各个实体之间的接触方式为粘接。当悬臂梁压阻传感器在自由端受50N的Z向力时,悬臂梁向上弯曲,最大Z向位移可达1.55mm,其应变及应力云图如图4和图5所示。
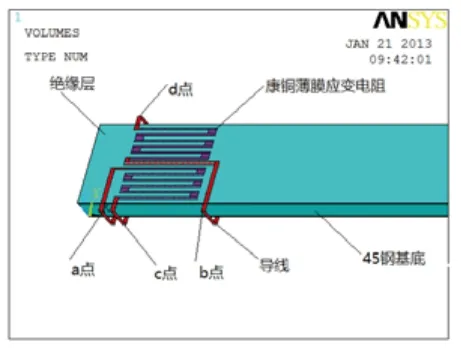
图3 传感器ANSYS模型图

图4 应变分布云图

图5 应力分布云图

图6 电场分布云图
在图3所示导线上a、b两点施加电压U0=5V,当悬臂梁产生应变后,由于R1、R2、R3、R4阻值的变化,图3中c、d两点之间会产生电势差。电场分布云图如图6所示,在图上测得c点电势为2.51338V,d点电势为2.4867V,两点间电势差Ucd=0.0267V,即为输出电压U1=0.0267V,通过式(2)可得出其电阻变化率=0.0053。
为研究电桥输出电压和电阻变化率与载荷之间的关系,分别在自由端加载1N、5N、10N、20N、50N、100N、200N的Z向力,测得电压输出值与力之间的关系图如图7所示,计算出电阻变化率与载荷之间的关系如图8所示。
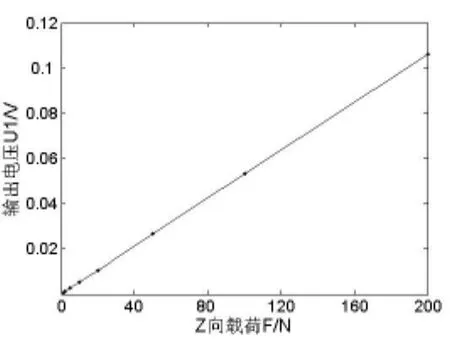
图7 输出电压与载荷关系图
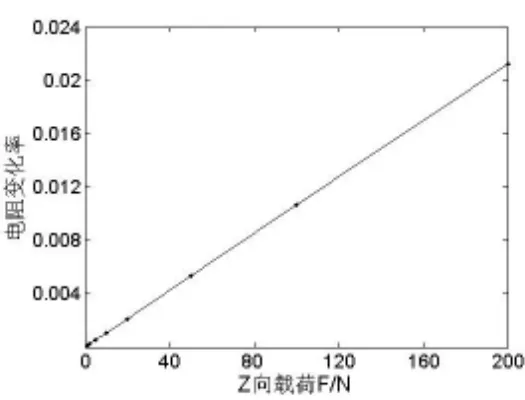
图8 电阻变化率与载荷关系图
由图7可以看出传感器输出电压U1与Z向载荷之间有着良好的线性关系,同理,由图8得出电阻变化率与载荷之间的线性关系。经拟合得电压与载荷间的线性关系式为 U1=1.07× 10-3FU0。
为分析传感器压阻薄膜位置及薄膜厚度与输出之间的关系,本文做了进一步的研究。图9是在50N的Z向载荷下,压阻薄膜厚度为0.5μm时传感器压阻薄膜距固定端的距离与输出电压之间的关系曲线。从图中可以清晰地看出当压阻薄膜距悬臂梁约束端越近时,其输出电压越大,传感器灵敏度越高,其变化值呈近似线性关系,这与图5中悬臂梁结构受Z向载荷时距约束端越近应力越大的结果相符。因此在设计传感器时,压阻薄膜位置应尽量靠近传感器约束端。
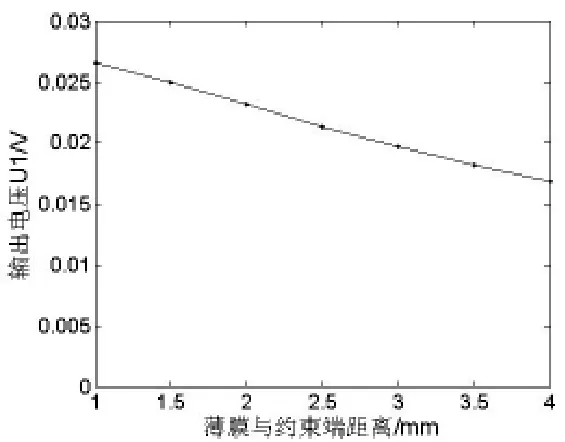
图9 输出电压与薄膜位置关系图
图10是在50N的Z向载荷下,压阻薄膜距悬臂梁固定端为1mm时传感器压阻薄膜厚度对输出电压的影响曲线。图中可以清晰地看出在一定厚度范围内传感器输出电压随着压阻薄膜厚度的变大而减小,但变化不是很显著,这与式(2)的结果相符,即薄膜厚度对传感器电阻变化率影响较小。
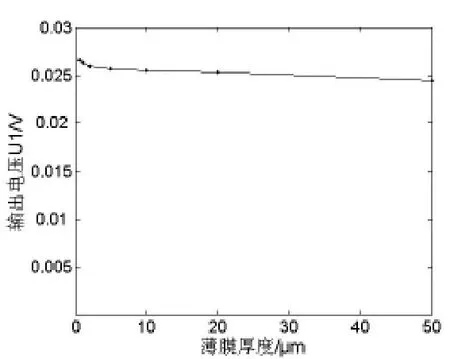
图10 输出电压与薄膜厚度关系图
4 结束语
本文设计了一种悬臂梁结构的薄膜压阻式传感器,并用ANSYS12.0软件对传感器的实际结构进行了静态特性的仿真分析。通过研究载荷与输出电压之间的关系得出了本传感器输出电压与载荷间的线性关系式 U1=1.07× 10-3FU0,由此得出了臂梁式压阻传感器具有良好的线性度和灵敏度的结论。同时分析了压阻薄膜位置和薄膜厚度对传感器输出的影响,发现压阻薄膜距悬臂梁约束端越近,输出电压越大,灵敏度也就越高,而薄膜厚度对传感器输出几乎没有影响。这些结论完全符合实际情况。因此,用ANSYS软件进行合金薄膜压阻传感器的研究是正确可靠的,具有较高的应用价值。完全可以将ANSYS软件应用于合金薄膜压阻传感器的研究工作中,以达到缩减研究成本、减少开发周期的目的,同时为下一步的实物研究做好了基础工作。
[1] 李伟,陈怀礼.合金薄膜高温压力传感器研究进展[J].火箭推进,2011,37(5):78-82.
[2] Hu Changyi,Gao Yiqun,Sheng Zhongyi. The piezoresistance coefficients of copper and copper-nickel alloys[J]. Journal of Materials Science,2000,35:381-386.
[3] Zhang Xugang,Li Xiaochun.Design and Characterization of Thin-Film System for Microsensors Embedding in Ti6Al4V Alloys[J].IEEE Sensors Journal,2010,10(4):839-846.
[4] 樊尚春,刘广玉.新型传感器技术与应用[M].北京:中国电力出版社,2010.
[5] 李伟东,吴学忠,李圣怡.一种压阻式微压力传感器[J].仪表技术与传感器,2006(7):1-5.
[6] 郑峰.常用金属材料手册[M].北京:化学工业出版社,2007,6:134-621.

