基于LM－BP神经网络的高铁建设环境中短期影响综合评价研究

孙东东

（石家庄铁道大学 研究生学院，河北 石家庄 050043）

高铁建设环境影响评价是一个多因素、多变量、模糊的非线性过程，其评价模型有许多种，如图形叠置法、指数法、网络法、矩阵法等等。但这些模型方法大多属于数学模型，存在着诸多不足，例如为了模型建立的方便，对复杂问题采取的简化处理降低了评价模型的准确性和有效性；指标权重主要依靠人为打分确定，主观性强；该类模型对评价的非线性拟合的差异不稳定，且可衡量性较差；基于此类模型开发的评价系统泛化能力弱、没有学习能力，灵活性、开放性、适应性也都较差［1］。

人工神经网络能模拟人的大脑活动，在非线性逼近、大规模并行处理、自组织和容错等方面具有极强的能力，所以在高铁建设环境干扰评价建模过程中应用人工神经网络会非常有效。在评价建模时，BP神经网络是应用最广泛的一类网络模型，但传统的BP网络在运算过程中采用的单一梯度算法容易出现局部极小、收敛速度慢等缺陷，从而限制了其应用推广。所以有必要拓宽思路，引入新算法优化BP神经网络，建立优质的高铁环境影响评价模型。

一、LM－BP神经网络

（一）LM 算法

为了最大程度避免传统BP神经网络的上述缺陷，利用Levenberg－Marquardt（LM）算法对神经网络进行训练学习，该算法融合了梯度算法和高斯—牛顿迭代算法的优点。使用LM算法的BP神经网络，即LM－BP神经网络，一方面克服了单一使用梯度算法造成局部极小、收敛速度慢的缺陷；另一方面降低了使用牛顿—高斯迭代算法时海塞矩阵在运算过程中变成奇异矩阵的概率。

LM－BP神经网络的两种算法是通过公式（1）进行智能融合的。

式中，E代表训练网络的误差；J为雅克比（Jacobian）矩阵，它里面包括了E对于权重W 和阈值的一阶微分；μ为自适应因子，当μ很小时，LM算法接近高斯—牛顿迭代法；当μ很大时，则接近梯度法。对于μ有如下调整方法：若E（n＋1）≥E（n），则有μ＝10μ；若E（n＋1）＜E（n），则有μ＝10／μ。

由公式（1）可知，运算每向前迭代一步，μ就相应的减小，在与误差目标接近的时候，该算法就接近于高斯—牛顿迭代法。使用高斯—牛顿迭代法时，在与误差最小值逐渐接近的时候，运算速度也逐渐更快，精确度也越来越高。实践证明，LM算法的训练次数明显少于梯度法等其他相关BP算法，在准确度方面也更有优势［2－4］。

（二）LM－BP神经网络训练步骤

再由隐含层传到输出层，最终输出结果为：

假设建立的网络结构为n－q－m，WIij（i＝1，…n，j＝1，…，q）表示为输入层第i单元到隐含层第j单元的权重，WHjk（j＝1，…，q，k＝1，…，m）表示为隐含层第j单元到输出层第k单元的权重，则θj（j＝1，…，q）为隐含层第j单元的阈值，θk（k＝1，…，m）表示为输出层第k单元的阈值，LM－BP网络算法学习过程如下：

步骤1 对权值和阈值进行初始化设置

初始化权值及阈值，将各权重和阈值设置为小的随机数。

步骤2 选定训练样本进行规范化处理

由于输入样本形式不一，为了建立统一的标准，必须对训练样本进行规范化处理，以免输入数据表达内容相差较大而造成失误。

步骤3 正向计算

设第P组样本，其输入样本为

Xn＝ （X1，…，Xn）T，期望输出为Ym＝ （Y1，…，Ym）T，P ＝1，2，…，L，是样本数量，则隐含层第j单元的输出为：

步骤4 计算网络的误差平方和E

设yp＝y1p，y2p，…，ymp为第P 组样本的实际输出结果。

则网络的误差平方和E可定义为：

对照给定的精度ε，看误差函数是否收敛，若收敛，则结束；如果不收敛则转向步骤5。

步骤5 反向计算

从输出层开始，采用非线性规划中的梯度法，按误差函数E的负梯度方向修改权系数，逐层调整权值，即：

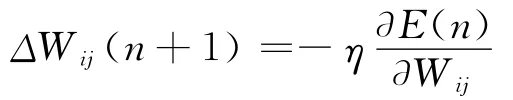
其中η称为步长或学习率。η的引入是为了加快网络的收敛速度。通常权值修正公式中还需加一个动量参数，以增加学习的稳定性。从而第n次学习时权值的修改公式变为：

步骤6 不断重复步骤3～5，直到样本的输出误差满足［5］。

二、应用实例

（一）长益城际铁路

长益城际铁路是湖北省境内长沙至益阳的城际高速铁路，设计时速250km／h。城铁的修建会对沿线的生态环境产生了一定程度的影响，在水土保持、水资源、动植物存在、噪音、固体废弃物、大气环境、土地功能利用等方面表现突出。

（二）中短期环境干扰评价指标体系的建立

铁路建设会对沿线周围的水土流失、水环境、动植物生存、人类居住、大气环境、土地功能等方面产生一系列影响，根据高铁建设对生态环境各方面影响的相关分析，把长益城铁对环境的干扰分成两类，一个是生物影响指标，一个是环境影响指标。每个下面分别有若干二级指标，建立了相应中短期环境干扰的指标评价体系，如表1所示。

表1 高铁建设中短期环境干扰评价指标

（三）指标无量化

1.定量指标的无量纲化

定义x为指标值，y为评价值，即指标值的无量纲化值，且y∈ ［0，1］，x∈ ［a，b］，a，b分别为指标的最小及最大值，正向指标和逆向指标分别采用相应的无量纲化函数。

（1）逆向性指标的无量纲化函数：

（2）正向性指标的无量纲化函数：

2.定性指标的无量纲化

采用确定隶属度的方法对定性指标进行无量纲化处理。首先，确定评价集P，包含5个评价等级，即P＝（极小影响，较小影响，中等影响，较大影响，极大影响），确定各评价等级的评价尺度B ＝（B1，B2，…，B5），本研究采用的尺度为 B ＝（0.1，0.3，0.5，0.7，0.9）T。其次，采用模糊统计法确定评价指标相对评价集P的隶属度向量ri＝（rb1，rb2，…，rb5）。最后，在给定评价尺度 B 下，将评价指标隶属于评价集P各评价等级的隶属度向量ri与标准尺度B作点乘运算，得到评价指标无量纲化值ci，ci值利用如下公式计算：

（四）评价等级的确定

高铁建设环境影响中短期评价模型需要对结果划分评价等级，文章将影响程度分为5个等级，当在［0，0.2）区间，定级为极小影响；区间［0.2，0.4），定级为较小影响；区间［0.4，0.6），定级为中等影响；区间［0.6，0.8），定级为较大影响；区间［0.8，1），定级为极大影响，上述划分的区间为确定为各个等级的范围。

针对训练样本的取值，文章分别在这5个等级规定的区间内均匀取值，从而生成足够多的训练样本。规定每个区间的中间量即｛0.1、0.3、0.5、0.7、0.9｝为训练样本这五个等级的理论输出值，与上述等级一一对应，上述的范围即为其每个影响的最大及最小限值。

（五）LM－BP神经网络综合评价结果

此次建立的LM－BP评价模型主要需要考虑两个问题：一是所建神经网络的网络的层数；另一个是每层中的神经元的数目。本研究采用的是传统的三层模式，即输入层、隐含层以及输出层。本研究使用以影响的时间作为划分的2组数据作为输入值。研究共随机生成2组2 000个样本，在每一组中随机抽取各500个样本分别作为检验样本和测试样本，剩下的1 000个样本作为训练样本。输出值对应上述设定的5个等级范围，分别对应一一对应他们所代表的影响程度。通过LM－BP神经网络对所输入的数据进行不断学习而进行分析，从而归纳出评价值与评价标准之间的关系，建立适用于预测高铁对环境干扰的综合评价模型［6］。输入输出节点数和隐藏层节点数会直接关系到预测结果。本文所建立的网络模型输入层结点数取12，隐含层结点数取27，输出层结点数为1，即网络拓扑结构为12－27－1。网络模型的隐含层和输出层的传递函分别为Sigmoid型函数和purelin型函数。而学习步长取0.05，期望误差为1e－006，最大迭代次数为500。

训练时，先将样本进行规范化处理，采用LM学习算法对BP神经网络进行训练。将所有数据导入Matlab神经网络工具箱进行运算，让所建立神经网络自动进行训练学习，训练到475步时误差达到所设定的期望值。图1展示了训练过程中误差收敛的曲线。

图1 训练过程误差曲线

为了衡量该网络的泛化能力，本研究将所选取的测试样本带入该网络，得到测试样本的实际输出值。然后根据测试样本的实际输出与期望输出进行线性回归分析得出实际输出与期望输出的相关系数为是0.971 3。使用传统标准的BP神经网络进行上述运算，达到期望误差需要进行825次迭代运算，实际输出与期望输出的相关系数则为0.724 3。所以，经上述样本训练后得到的神经网络模型泛化能力很强，学习速度和精确度都有所提高，能很好地用于评价未知样本［7］。

使用以上建立好的LM－BP神经网络预警仿真预测进行评价，对高铁规划实施后的占用土地量和固体废物量等进行预测，对规划实施可能对生态环境、声环境、水环境以及生态敏感区等方面的环境影响进行分析，最终得到高铁建设环境影响评价的指标特征、无纲量化值，如表2所示。

表2 各指标量化值

三、结论

建立了高铁建设对环境影响的综合评价模型，并对其进行了反复学习训练，只需要将量化完成的评价值输入已经训练好的模型，经运行后可得到高铁建设对环境影响的综合评价值。分别得到短期和中期影响的实际输出值为0.372、0.223，得到长益城铁建设对沿线环境的影响程度分别为较小影响和极小影响。

使用LM算法的神经网络评价模型，相对传统单一使用梯度算法的神经网络模型，其收敛速度和精确度都有所提供。所以LM－BP神经网络评价模型的应用可提高评价结果的客观性和准确性，从而为高速铁路的选线决策提供了科学的评价方法。

［1］郭富强.基于径向基函数网络的教师教学质量评价［J］.价值工程，2012（18）：170－171.

［2］BISHOP C M.Neural networks for pattern recognition［M］.Oxford：Clarendon Press，2009：5－28.

［3］ANDERSON J A.An Introduction to neural networks［M］.London：MIT Press，2010.

［4］贺昌政，李晓峰，俞海.BP人工神经网络模型的新改进及其应用 ［J］.数学的实践与认识，2009，32（4）：554－561.

［5］AVSAR Y A，SARAL M T，GONULLU E，et al.Neural network modeling of outdoor noise levels in a pilot area［J］.Turkish J.Eng.Environ.Science，2010，28：149－156.

［6］MARZABAN C，STUMP G J.A Neural Network for Tornado Prediction Based on Doppler Radar－Derived Attributes［J］.Journal of Applied Meteorology，2011，35：617－626.

［7］江学军，唐焕文.前馈神经网络泛化能力的系统分析［J］.系统工程理论与实践，2009，20（8）：36－40.