单相变压器参数测定中试验表计不同接入方式的影响

申一先,方赞峰

（北京交通大学电气工程学院,北京100044）

单相变压器作为一种重要的电工电子部件,在电力系统、自动化设备和电子行业等领域应用广泛,其性能直接影响设备的正常运行.反映变压器性能优劣的是参数指标,根据变压器等效参数,计算出变压器在运行过程中的效率,检验变压器的性能是否满足要求[1].通过空载试验和短路试验,能够测出变压器的空载损耗、空载电流和短路阻抗,验证变压器铁心的设计计算、工艺制造是否满足技术条件和标准的要求,检查变压器铁芯是否存在缺陷,如局部过热、局部绝缘不良等[2].因此变压器参数测定方法选择显得至关重要,采用科学合理的试验表计连接方法,可以获得高准确度的测量数据[3].本文通过理论分析和试验验证研究了单项变压器空载和短路试验中表计对参数测定的影响,并得出正确的表计接法电路以供参考.

1 空载试验

空载试验能够测量并计算出电压比K、空载电流I0、空载损耗P0、励磁电阻Rm和励磁电抗Xm等参数[4].加额定电压时,铁芯材料处于饱和状态,此时变压器等效阻抗Z很大[5].

1.1 空载试验接线电路的理论分析

空载试验接线电路模型及其等效电路如图1所示,空载试验中通过变压器中的电流很小,电压表中的电流不能够被忽略.

设I1、I2、I3为各模型中实际电流表测量的电流值,I0、IWI、IV分别为经过变压器、功率表、电压表的电流；Z1、Z2、Z3为各模型计算时所得到的阻抗值,其中 RWI、RWV、RV、RI分别为功率表电流线圈电阻、功率表电压线圈电阻、电压表内阻、电流表内阻.在空载模型I中,I1=I0,电流表的内阻RI相对于变压器阻抗Z很小可以忽略不计,所以,Z1=RWI+RI+Z≈Z,即测算出来变压器阻抗的测量值约等于实际值；在空载模型II中,I2=I0+IWI,Z2=（RWI+Z）∥Rwv≈Z∥Rwv＜Z1,的阻抗Z2小于Z1,测量阻抗比实际值小；在空载模型III中,I3=I0+IWI+IV,Z3=（RWI+Z）∥RWV∥RV≈Z∥RWV∥RV=Z2∥RV＜Z2,测得变压器阻抗 Z3＜Z2,其误差空载模型Ⅱ更大.因此,电压表的分流不能忽略,电流表外接时所得数据误差较大.

1.2 空载试验接线电路验证

通过试验数据分别测算出空载模型II和III的参数,并以空载模型I的测算参数为基准与其对比,验证上述理论分析.实验时所采用的单相变压器：额定容量为1 kW,额定电压为220/110 V,额定电流为4.5/9 A.

1.2.1 电压-功率特性曲线 电压-功率特性曲线见图2.

3种接法在外加电压相同时功率相等同,说明3种模型在同一电压下的工作状态相同,因此空载试验中电流表（或功率表）的位置对电压测量的准确性没有影响.

1.2.2电压表分流验证 电压-电流特性曲线见图3.

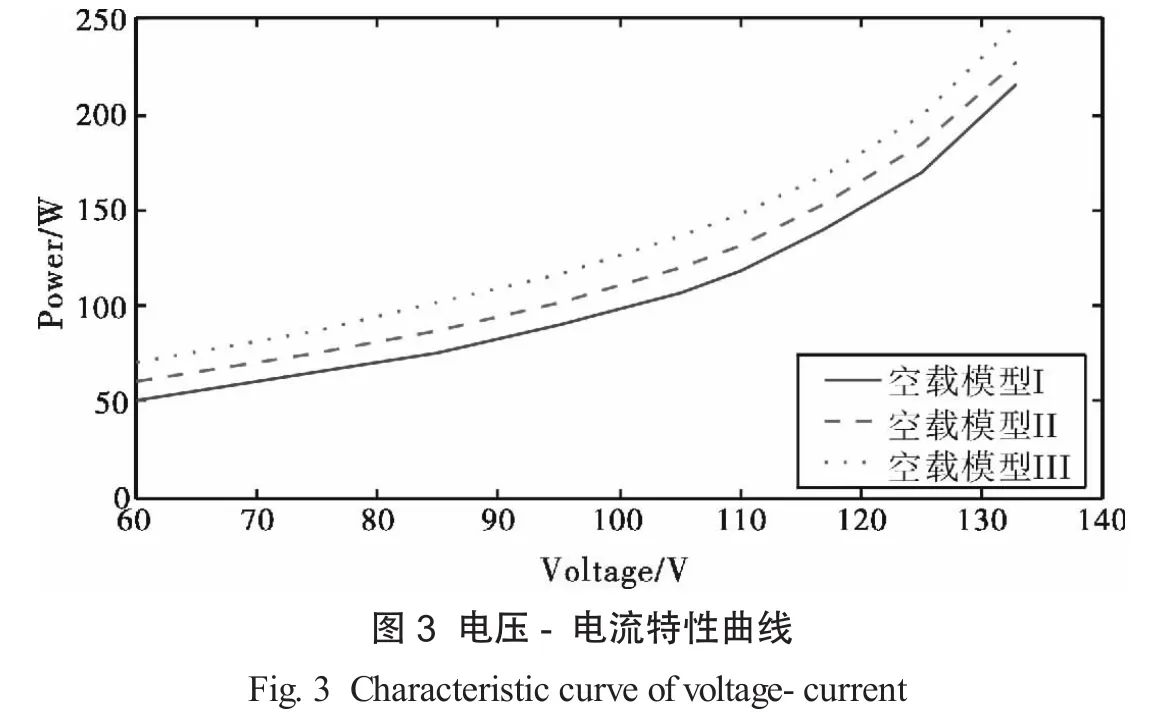
3条曲线的变化趋势相同,仅仅在垂直方向有平移,验证了电流分流关系式：I1=I0,I2=I0+IWI,I3=I0+IWI+IV.因此在空载试验中流经功率IWI和电压表的电流IV是不可忽略的.

1.2.3 结果分析 空载试验数据及计算参数结果如表1所示.

表1 空载试验数据及结果Tab.1 Data and results ofno-load test

由表1可知,对于空载模型II,电流测量受到功率表IWI分流影响：I2=I0+IWI（IWI=10.57%·I0）,电流测量的误差影响变压器参数的计算.导致后续计算时Z2=0.906·Z,R的误差达到△R=19.18%.可见在进行变压器空载试验时,电流表要内接于功率表.

对于空载模型III,相对于空载模型II电流测量多受到电压表IV分流影响：I3=I0+IWI+IV（IWI+IV=24.68%·I0）,导致计算结果产生更大的偏差,因此电流表也要内接于电压表.

空载试验时,流经变压器电流为毫安级,电流表测量易受电压表IV和功率表IWI分流的影响,电流表必须内接,即直接串在变压器上；同理,为了防止功率表所测电流受电压表IV分流影响,电压表要外接于功率表.只有空载试验模型I能较准确地测算出变压器参数.

2 短路试验

通过短路试验,能够测量计算出短路电压Uk、短路电阻Rk、短路电抗Xk和短路损耗Pk4个参数.短路试验通常在高压侧加额定电流,低压侧短接,此时变压器的阻抗很小[6].

2.1 短路试验接线电路的理论分析

短路试验接线的电路模型及其等效电路如图4所示,短路试验中变压器两端的电压很小,电流表的分压是不能被忽略的[7].

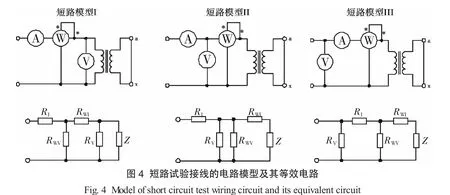
设U1、U2、U3为各模型中实际电压表测量的电压值,U0、UWI、UI分别为变压器、功率表侧电流线圈、电流表两端的电压.在短路模型I中,U1=U0,Z1=Z∥RV·RWI/｛RWV+RWI+[RV/（RV+Z）]｝=Z-△1,变压器阻抗Z与电压表、功率表电压线圈电阻相比极小,并联后总阻抗较变压器的真实值略小△1；在短路模型II中,U2=U0+UWI,Z2=（RWI+Z）∥RWV∥RV≈RWI+Z,RWI相对变压器阻抗Z不可忽略；而在短路模型III中,U3=U0+UWI+UI,Z3=RI+（RWI+Z）∥RWV∥RV≈R I+RWI+Z,RWI、RI不可以忽略,所测阻抗实际值偏大.综上所述,电压表外接于电流表时产生较大误差.

2.2 短路试验接线电路验证

通过试验数据计算出空载模型I和II的参数,并与空载模型III的测算参数对比,验证上述理论分析.实验时所采用的单相变压器：额定容量为1 kW,额定电压为220/110 V,额定电流为4.5/9 A.

2.2.1 电流-功率特性曲线 短路电流-功率特性曲线见图5.

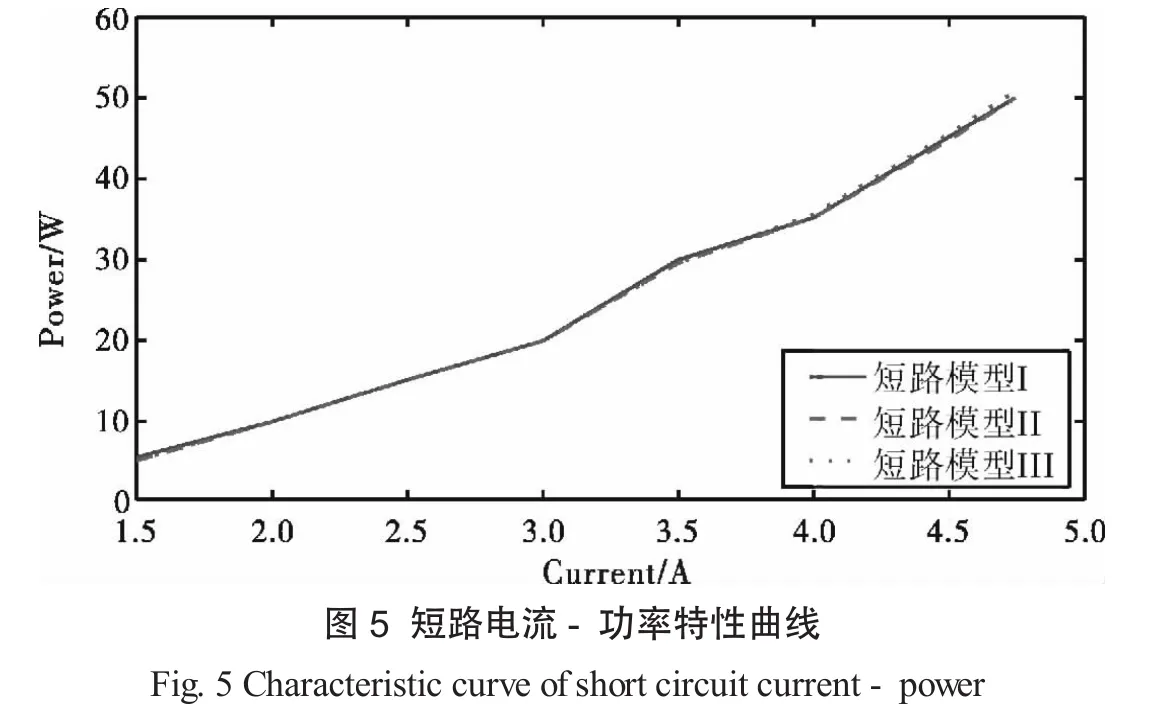
3种接法在流经变压器电流相同时功率相等同,说明三种模型在同一电流下的工作状态相同,因此短路试验中电压表（或功率表）内接于电流表对电流测量的准确性没有影响.

2.2.2 电流表分压验证 短路电流-电压特性曲线见图6.

短路模型I和II的特性曲线差别极小,短路模型III同前两者相比差别较大,说明功率表的分压UWI很小可以忽略,而电流表的分压UI对试验结果的影响不可忽略,即试验实际测量电压值：U1=U0、U2=U0+UWI≈U0、U3=U0+UWI+UI≈U0+UI.

2.2.3 试验结果分析 短路试验数据及结果如表2所示,由理论分析知Z1=Z-△1＜Z2=RWI+Z,试验结果为|ZK1|=2.333≈|ZK2|=2.367,证明△1和RWI相对于变压器阻抗Z很小,因此短路模型I和II系统误差可以忽略.

表2 短路试验数据Tab.2 Short circuit experiment data

由表2可知,短路模型III相对于短路模型I来说,其△U=6.19%、△Z=6.215%、△R=1.125%和△X=46.98%；短路模型III相对于短路模型II来说,其△U=4.69%、△Z=4.689%、△R=2.229%和△X=19.02%.从短路电流-电压特性曲线和误差对比可知,短路模型III的系统误差较大,所得变压器的参数与实际值差距很大,不应被采用.短路试验电压表所测变压器两端电压易受到电流表分压的影响,电压表必须内接于电流表.同理为防止功率表测量电压受电流表分压的影响,功率表必须接于电流表内侧.而功率表分压对电压表所测数据影响不大,功率表和电压表的相对位置并不受限制.短路试验模型I、II存在极小的系统误差可以忽略,因此两种模型都可得到准确的结果.

3 小结

本文给出了单相变压器空载试验、短路试验中试验表计的不同接法的电路结构,从理论推导和实验验证两方面研究了试验表计在不同接入位置对试验结果准确性的影响.结果表明：空载试验中模型I所测量数据最为准确,即变压器副边先串联电流表再接功率表最后外并电压表；短路试验中模型I和II测量数据准确,即电流表串接在最外侧,而电压表和功率表的相对位置不受到限制.

[1]刘慧娟,张威.电机学与电力拖动基础[M].北京：国防工业出版社,2007.

[2]刘慧娟.电机学[M].北京：北京交通大学出版社,2012.

[3]邬伟民,梁恒基.检测变压器动稳定状态参数的物理基础和实际意义[J].电力设备,2002,3（4）：38-42.

[4]李自良.变压器等效电路的类型和阻抗参数的分析与变换[J].变压器,1997,34（3）：25-29.

[5]陈科.变压器结构参数计算：变压器基础知识之二[J].电子变压器,1989（4）：31-38.

[6]刘传彝,侯世勇,许长华.电力变压器设计与计算（1）[J].变压器,2011,48（2）：54-55.

[7]戴文进,杨莉.电机学导学导教[M].北京：清华大学出版社,2010.