摄动连续矩阵方程解的下界

王 春， 陈东彦， 王 影， 孙 飞， 孙 璐

(1.黑龙江科技学院 理学院，哈尔滨 150027;2.哈尔滨理工大学 应用科学学院，哈尔滨 150008;3.黑龙江科技学院 工程训练与基础实验中心，哈尔滨 150027)

0 引言

代数Riccati和Lyapunov矩阵方程的求解问题广泛应用于系统稳定性分析、时滞系统的控制器的设计、最大成本估算、数值算法的收敛性等许多控制难题中，具有重要的理论和实用价值。针对离散和连续Riccati矩阵方程的研究已取得一些成果[1－3]。但由于在实际情况中存在不可避免的建模误差等问题，因而，估计不确定Riccati矩阵方程解的界更具有实用价值。目前，已有对摄动离散矩阵方程的研究[4－5]，但针对摄动连续矩阵方程的研究较少，其中，文献[6]利用矩阵不等式等估计了摄动连续Riccati方程解矩阵的界，文献[7]利用矩阵运算等性质给出了摄动连续矩阵方程的界。因此，笔者在文献[6]的基础上，利用矩阵不等式及特征值的性质等估计了摄动连续Riccati和Lyapunov矩阵方程解矩阵的下界。

1 问题描述

考虑摄动连续Riccati矩阵方程:和摄动连续Lyapunov矩阵方程:

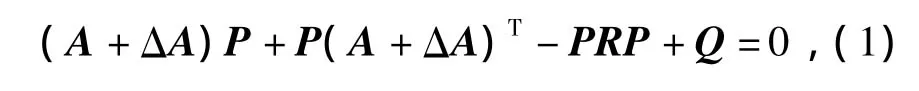
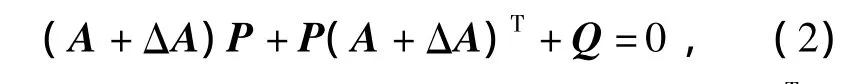
其中，A∈n×n为渐近稳定矩阵，Q∈n×n，Q=QT＞0和 R∈n×n，R=RT＞0均为对称正定矩阵，(A+ΔA)稳定，ΔA∈n×n为不确定矩阵，表示矩阵A的结构摄动，且假设ΔA∈n×n满足范数有界不确定性，即

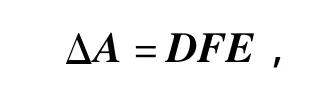
其中，D∈n×s，E∈l×n为已知的常值矩阵，F∈s×l为相应维数的未知不确定矩阵，满足FTF≤I，I为相应维数的单位矩阵。

文中，λi(X)为矩阵 X∈n×n的第 i(i=1，2，…，n)个特征值，设矩阵X=XT，X∈n×n的特征值按递减顺序排列，即 λ1(X)≥λ2(X)≥…≥λn(X)，XT表示矩阵X的转置，tr X表示矩阵X的迹，det X表示矩阵X的行列式。

2 预备知识

引理1[8]设A，D，E和F是相应维数的矩阵，且FTF≤I，则对任意正定矩阵R＞0和任意满足R －εDDT＞0的正数 ε ＞0，有

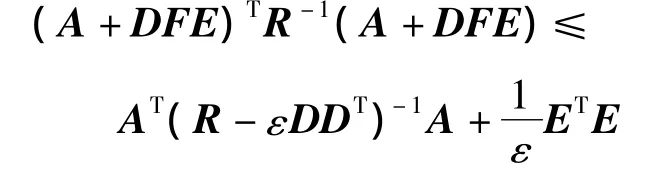
成立。

引理2[9](Schur补引理) 矩阵这里W=WT和V=VT与不等式(i)或(ii)等价:

(i)V ＞0，W －SV－1ST＞0，

(ii)W ＞0，V －STW－1S ＞0。

引理3[10]对于任意的变量x∈n和矩阵X∈n×n，有

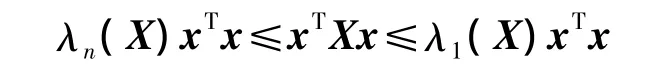
成立，从而有λn(X)In≤X≤λ1(X)In成立。

3 主要结果及证明

定理1 设矩阵P为方程(1)的唯一正定对称解矩阵，则P满足不等式:

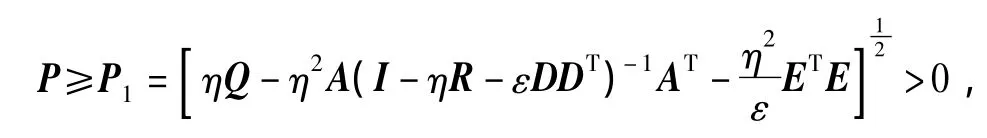
其中，对任意的ε＞0和η＞0满足下列不等式成立:

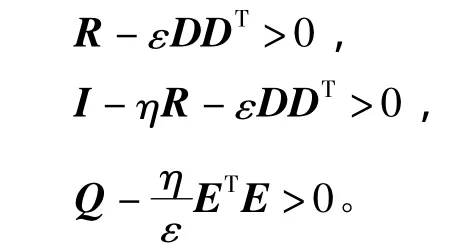
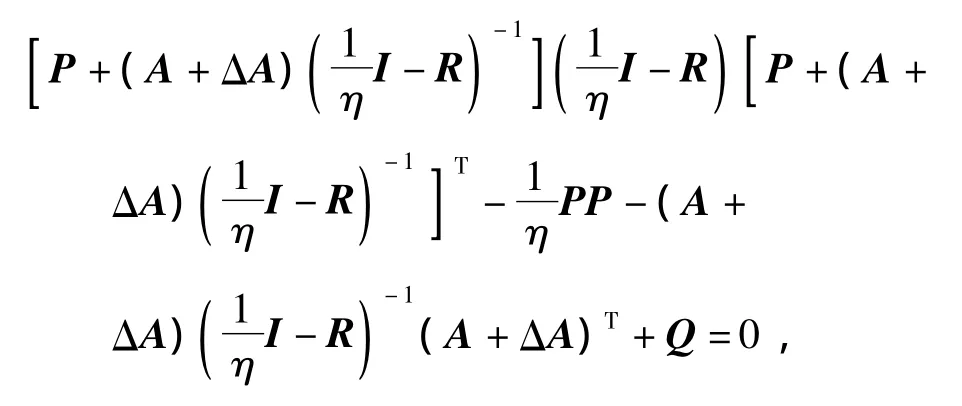
移项可得，

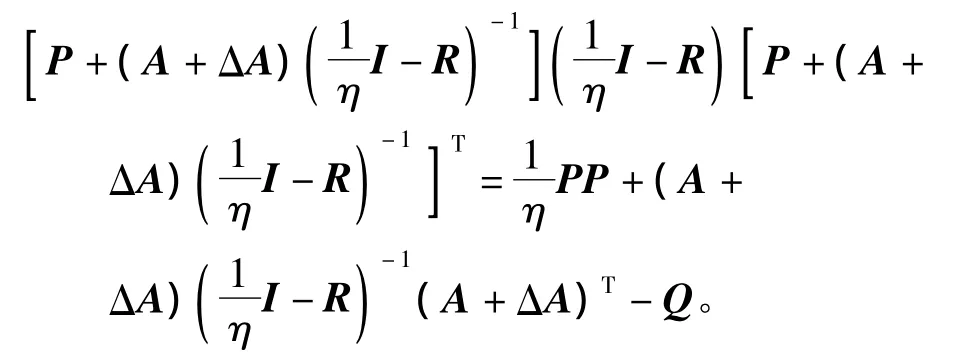
如果对任意的η＞0满足I－ηR＞0，则有下列不等式成立

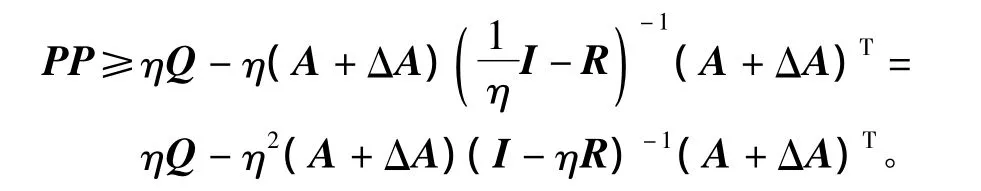
由引理1，对任意的满足I－ηR－εDDT的正数ε＞0有

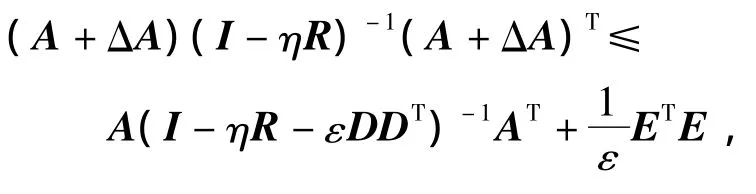
从而有，

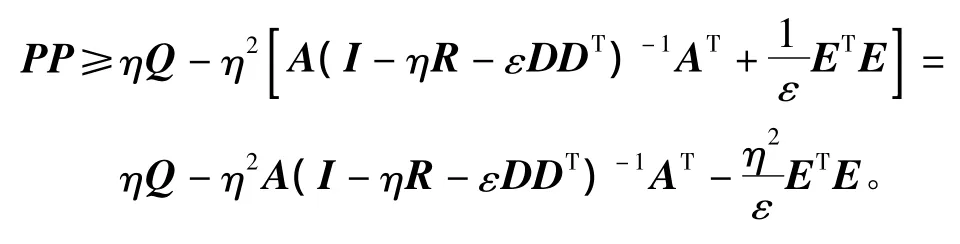
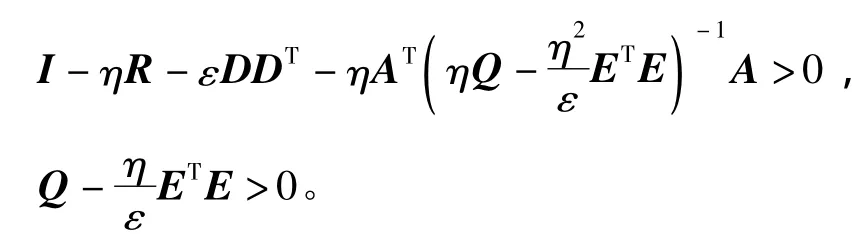
使用引理2，可以得到

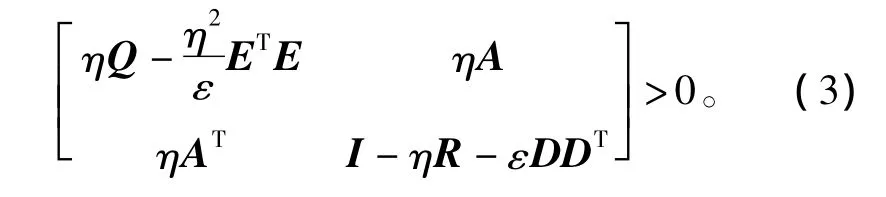
从而由式(3)可得

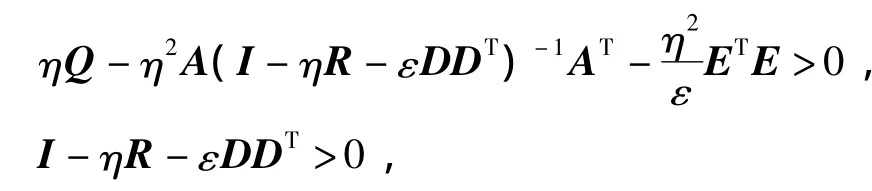
则有

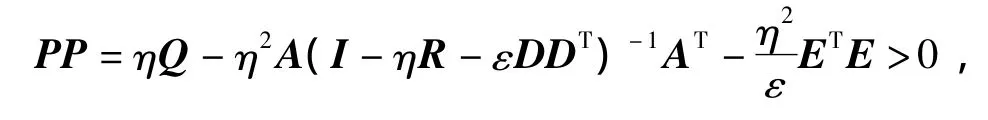
则可得P的下界

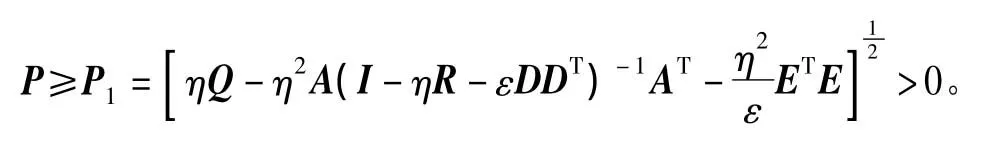
证毕。

推论1 设矩阵P为方程(1)的唯一正定对称解矩阵，则P满足不等式:

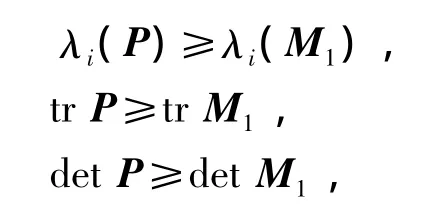
这里的矩阵 M1为 M1[= ηQ－η2A(Ι－ηR－

推论2 设矩阵P为方程(2)的唯一正定对称解矩阵，则P满足不等式:

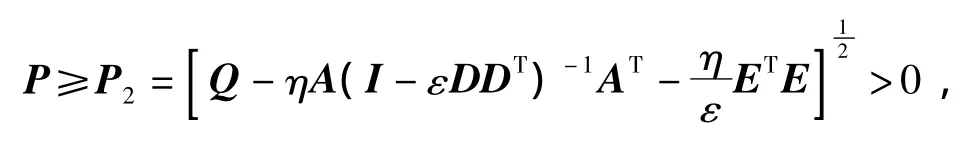
其中，对任意的ε＞0和η＞0满足I－εDDT＞0及

定理2 摄动连续Lyapunov矩阵方程(2)中，设矩阵Q=QT是正定矩阵，A是稳定的，A+ΔA为非奇异矩阵，则其唯一的正定对称解矩阵P具有下界:

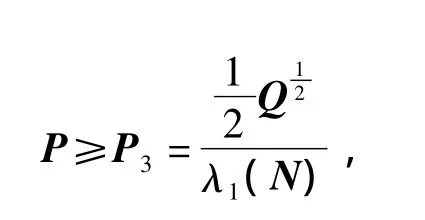
其中，对任意的 ε＞0满足 Q－εDDT＞0，且矩阵N为

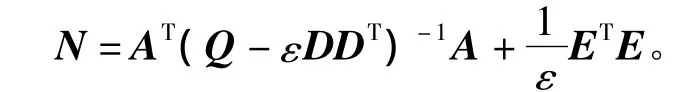
证明 令矩阵 U=[(A+ΔA)－1Q(A+，即可得

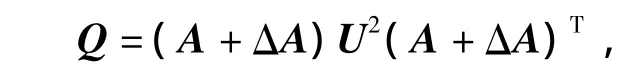
然后用U－1分别左乘和右乘式(2)，得

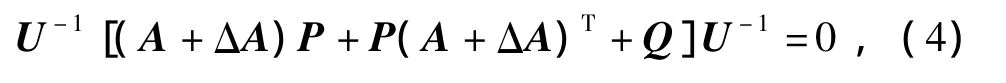
对式(4)两端加

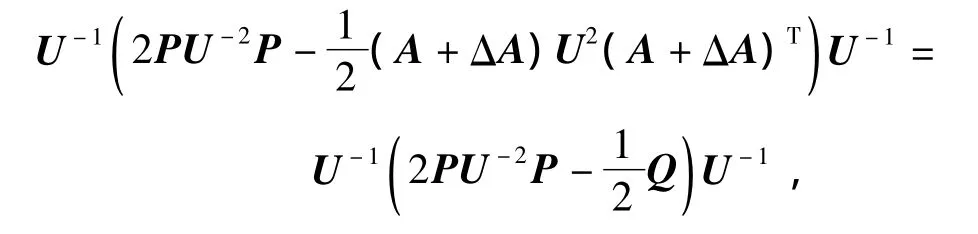
可以得到

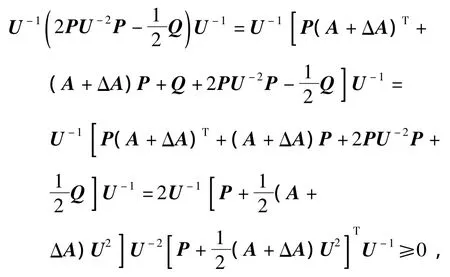
则可得到

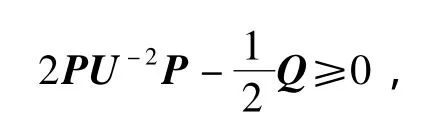
从而有

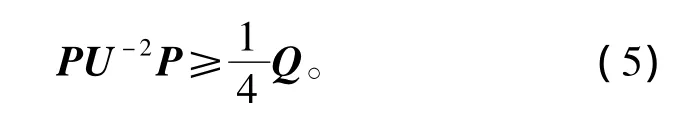
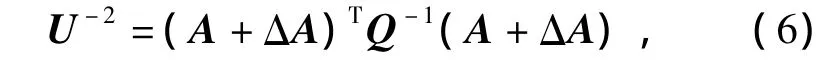
将式(6)代入式(5)，可得

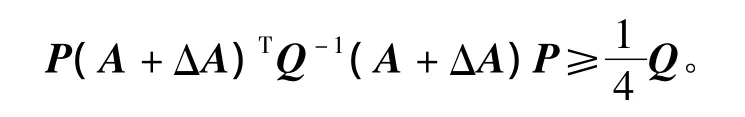
而由引理1，有

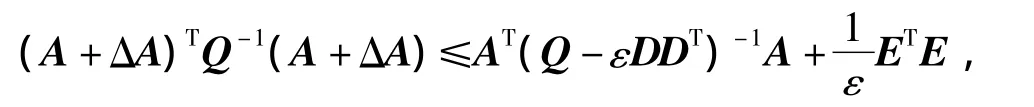
即有

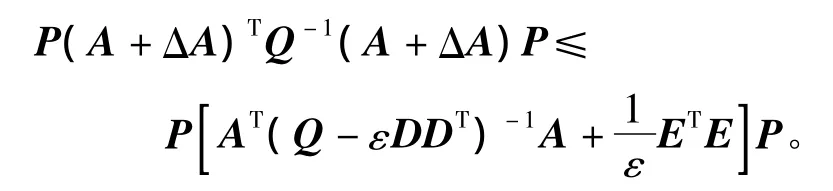
利用引理3中X≤λ1(X)I，得

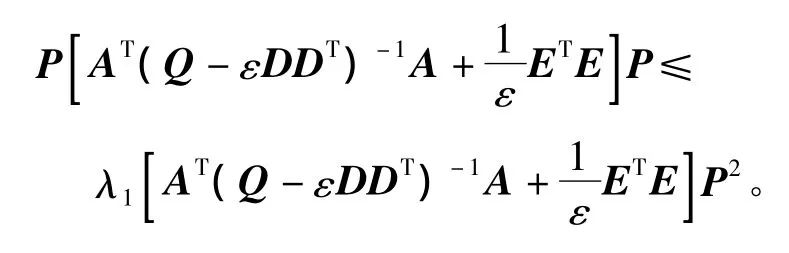
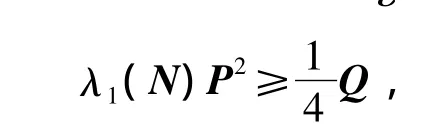
从而可得解矩阵P的下界为

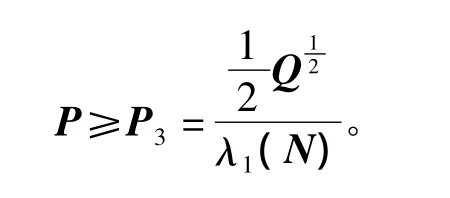
证毕。

推论3 设矩阵P为方程(2)的唯一正定对称解矩阵，则P满足不等式:

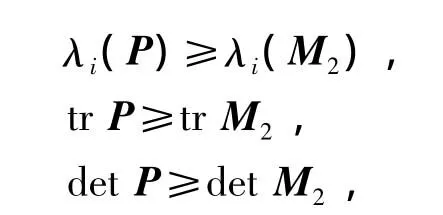
这里的矩阵 M2为，矩阵 N与定理2同。

4 数值算例

例1 在方程(1)中，设ΔA∈n×n满足范数有界不确定性，且

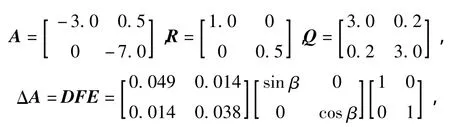
利用定理1，取 ε=0.7，η=0.055，得方程(1)解的下界为

该结果与文献[6]相比具有更小的保守性。

5 结束语

文中对摄动连续Riccati和Lyapunov矩阵方程的解的下界进行了估计。其中摄动参数满足范数有界不确定性，利用矩阵不等式和Schur补引理等知识，得到了解矩阵的下界，且根据该结果，可以对摄动连续矩阵方程的解进行估计，最后利用数值算例说明了所得结果比已有结果具有更小的保守性。摄动参数满足非结构不确定性等其他不确定性的摄动连续和摄动离散Riccati矩阵方程的解的上下界问题，将是进一步的研究课题。

[1]张端金，杨成梧.离散代数Riccati方程解的上下界研究[J].信息与控制，1998，27(1):23－25，31.

[2]段福兴，沈 轶.离散代数Riccati方程解的上下界[J].应用数学，2000，13(2):95－97.

[3]周喜华，肖志涛.基于连续Riccati方程解的界的估计[J].吉首大学学报:自然科学版，2008，29(3):26－28.

[4]陈东彦，侯 玲.摄动离散矩阵Lyapunov方程解的估计[J].控制理论与应用，2006，23(5):830－832.

[5]王 春，陈东彦，王 影，等.摄动离散Riccati矩阵方程解上界估计[J].辽宁工程技术大学，2012，31(6):905－908.

[6]王 春.摄动连续Riccati矩阵方程解矩阵界的估计[J].科技导报，2010，28(19):59－61.

[7]毕海云.代数Lyapunov方程与Riccati方程解的估计[D].哈尔滨:哈尔滨理工大学，2008:27－37.

[8]MOHEIMANI S O R，PETERSEN I R.Optimal quadratic guaranteed cost control of a class of uncertain time-delay systems[J].IEEE Proceedings Control theory Application，1997，144(2):183－188.

[9]KREINDLER E，JAMESON A.Conditions for nonnegativeness of portioned matrices[J].IEEE Transactions on Automatic Control，1972，17(1):147－148.

[10]RUGH W J.Linear system theory[M].Upper Saddle River，NJ，USA:Prentice-Hall，1993:237 －241.