基于无源RFID的最小包容圆自适应定位法

边江南，刘洪武

(南昌航空大学信息工程学院，江西 南昌 330063)

0 引言

无线传感器网络的飞速发展使得人们对室内定位的需求不断增长。RFID定位技术具有非接触式和非视距操作的特点，除了安全性和灵敏度很高以外，还可利用标签传递大量的信息，因此它被广泛应用在室内定位领域。

LANDMARC定位法[1]利用参考标签辅助定位的方法可以减少阅读器的数量，降低成本的同时又可以提高定位精度。通过K临近法来建立信号强度和能量级别之间的关系，可以降低环境因素对系统定位性能的影响。文献[2]将LANDMARC定位法中的有源参考标签用成本更低廉的无源参考标签取代，使得在不增加系统成本的情况下增加参考标签的数量，提高了定位精度。文献[3]对参考标签布设的拓扑结构进行分析，得出了一种减小定位区域的参考标签布设方法，可以有效提高定位的精度。文献[4]的自适应K临近算法提高了系统对环境的应变能力，使得定位效果更加稳定可靠。

在K临近法消除一定原因造成的基础上，随机误差使得定位的估计位置随环境变化呈现出随机分布的现象，本文提出的利用最小包容圆[6]的圆心估计待测定位置的方法可以有效地减小这种随机误差，进一步提高定位的精确度。

1 LANDMARC定位法

1.1 LANDMARC 原理

LANDMARC(Location Identification Based on Dynamic Active RFID Calibration)是基于有源RFID参考标签辅助定位的一种室内定位法。其阅读器、参考标签和待测标签的布设如图1所示。

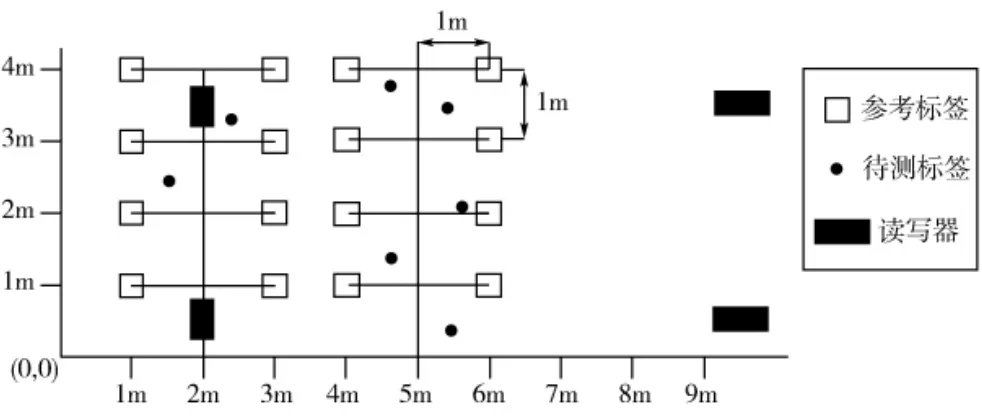
图1 LANDMARC系统阅读器和标签布设结构

假设有n个阅读器，m个参考标签，u个待测标签。对于同一个参考标签，定义读写器测得的待测标签的信号强度矢量为:

对于每个待测标签p，p∈(1，u)，信号强度的欧式距离rj为:

然后用K临近算法计算待测标签的坐标。该算法从极限原理的角度出发，用一个样本在特征空间中的K个最相似样本来判别该样本的所属类别。对于待测标签的坐标来说，以参考标签的坐标为特征空间，选择信号强度特征与之最相似的K个点来判别待测标签所在位置:

其中加权值wi为:

1.2 LANDMARC算法的评估

如图1所示，LANDMARC算法没有对参考标签布设的拓扑结构进行分析，而实际上它的拓扑结构对定位精度有一定的影响。LANDMARC算法在运用K临近法选取临近参考标签时的K值是由大量对现时实验环境的测试来确定的，这种方法对于复杂变动的实验环境存在着很大的局限性。LANDMARC算法可以配合其它优化算法使得定位精度得以进一步提高。

2 自适应定位法

本文所采用的自适应RFID定位法用无源RFID参考标签在室内环境内布设，采用优化的拓扑结构，构成定位系统的已知固定条件，然后以原始LANDMARC算法为基础，使用自适应K临近法进行K值的选取，来估计待测标签的坐标，使得算法具有智能性，再将多次估计的坐标点所构成的点集用最小圆包容算法找到其点集的最小包容圆所在的圆心，来作为最终的待测标签的估计坐标。自适应定位法的系统构成如图2所示。

图2 自适应定位法系统构成

2.1 拓扑结构优化

LANDMARC定位法利用参考标签辅助定位，其参考标签的布设结构称之为参考标签的拓扑结构。一般要在计算待测点坐标前选取K个最邻近点来辅助估计结果。LANDMARC定位法的参考标签拓扑结构如图3中的矩形网络形式所示。定义由所选取的最邻近的K个参考标签所围成区域为待测标签的定位误差分布区域。文献[3]中分析其矩形的形状和定位误差分布区域以及定位精度三者的关系得出两点结论:(1)当所选定的K值确定后，存在争议的最邻近点的替换不能改变待测标签的误差分布区域大小。如当K值为4，选择最邻近的4个点是BOFH或HODF两种方案的定位误差分布区域是相同的;(2)随着矩形边长的增加，待测标签的定位误差分布区域也相对增大，使得定位精确度降低。当矩形为正方形，K值为4时，定位误差分布区域有2/3的概率为矩形，另外1/3概率为等腰三角形。

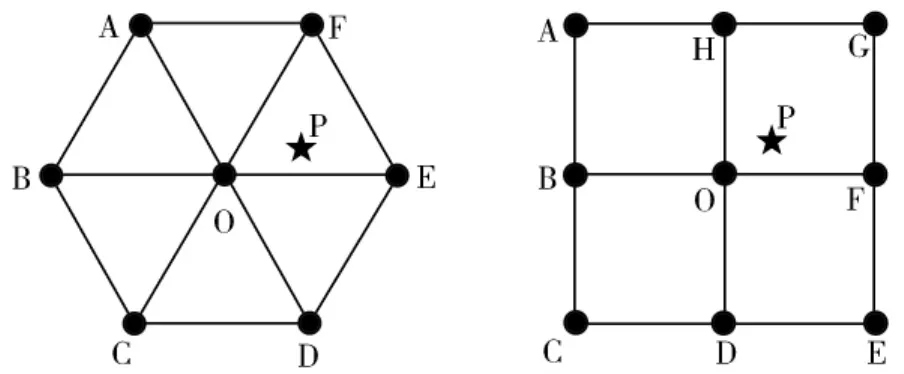
图3 两种参考标签的拓扑结构

若参考标签的拓扑结构布设成如图3中的正三角形网络的形式，毫无疑问与待测标签P最邻近的3个点不存在争议，定位误差分布区域为OFE围成的三角区域。由于不会增加待测标签的定位误差分区区域，所以可以相对提高定位精确度。

2.2 自适应K临近算法

基于LANDMARC定位法的原始K临近算法的K值是在特定实验环境下所测得的适合值。但是在复杂多变的实际应用环境中，系统的最佳K值不是一个常数。为了提高实时定位的精确度，选取的K值应该适合实时的环境条件。

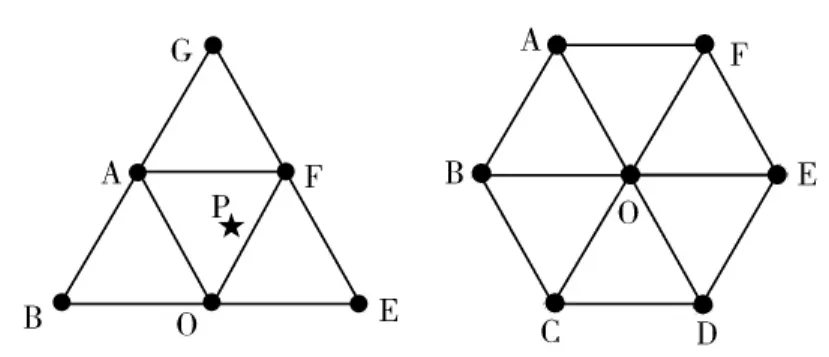
图4 自适应K临近法的拓扑局部结构(K=3，4，5，6)

如图4所示，在三角形拓扑网络结构中，待测标签P的定位误差分布区域为正三角形。当选择K=3时，定位误差分布区域为三角形AOF;当选择K=6时，定位误差分布区域为三角形GBE。而选择自适应K值时的拟待测标签O在K=6时对应的定位误差分布区域为正六边形ABCDEF。考虑到最佳K值可能在不同时刻有不同值，将K的可能值设置为4到6之间的可变值，其算法流程如图5所示。

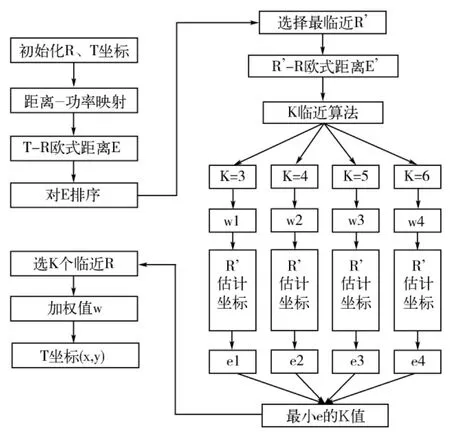
图5 自适应K临近算法流程

自适应K临近算法不但充分利用了三角形拓扑网络的有利条件，而且对变动的应用环境有了更强的适应性，提高了实时定位精确度。

2.3 点集最小包容圆定位法

LANDMARC算法的优点在于，它是基于极限趋近思想的一种算法，通过对选区的K个临近点加权计算，得到待测标签的坐标。由于参考标签和待测标签有着相同的物理结构，这样就在一定程度上消除了参考标签和待测标签某些共同因素引起的误差，即相对误差。但是估计出的待测标签的坐标还存在着随机误差。如果采用极限的思想考虑，当对一个位置固定的待测标签重复测定位置的次数趋近于无穷大，那么估计坐标描点后的分布区域为一个以实际待测标签坐标为圆心的圆形区域。

采取逆向思想考虑问题，将多次估计出的待测标签的坐标点集用一个最小包容圆将它们圈起来，令其圆心作为估计的待测标签的坐标。这样就可以将定位随机误差大大的削减。该算法的步骤为:

(1)在估计点集中任取3个点A、B、C;

(2)作一个包含A、B、C三点的最小圆，圆周可能通过这3个点，也可能只通过其中两个点，但圆包含第3点;

(3)在点集中找出距离(2)所建圆圆心最远的点D，若D点在圆内或圆上，则该圆即为所求圆，算法结束，否则执行(4);

(4)在A、B、C、D中选3个点，使由它们生成的一个包含这4点的圆为最小，这3点成为新的A、B、C三点，返回继续执行(2)，一直到找到所求最小包容圆。

3 仿真分析

本文的自适应定位法也是一种基于RSSI的算法，所以有必要建立读写器接收到的功率和距离间的映射模型。在此基础上，用Matlab2011a搭建系统的软件仿真平台，分析本文的算法是否能够有效提高定位的精确度。

3.1 模型

本文采用文献[5]中所描述的对数正态路径损耗模型，建立读写器的接收功率和距离间的映射关系。路径损耗PL(d)表示为:

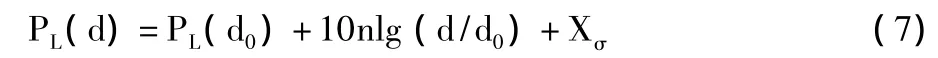
其中，d为测定点到发射点的距离，d0为参考距离，PL(d0)为发射点到参考距离间经历的路径损耗，n为路径损耗指数，Xσ均值为0，方差为σ2的高斯随机变量。在本文的仿真中，令读写器的发射功率为30dBm，路径损耗指数为1.8，标准差 σ =5.2 dB。

3.2 仿真和调试

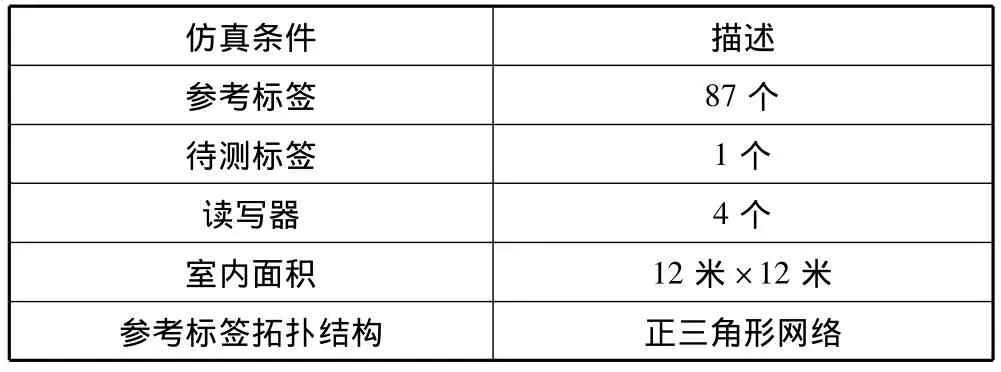
表1 仿真环境的组建

模拟一个长宽均为12米的室内环境，将参考标签、读写器和待测标签均设置在其中。实验涉及的因素如表1所示。布设结构如图6所示，首先将读写器放置在矩形4个角，将参考标签在矩形范围内布设成三角形拓扑结构，最后将待测标签放置在矩形区域的任意点处。

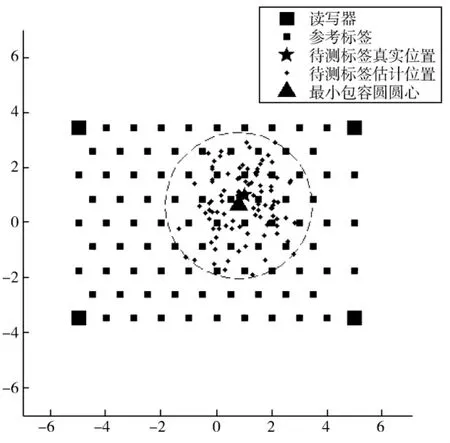
图6 自适应定位法仿真

(1)初始化标签坐标，待测标签出现在图6所示的定位区域中的(1，1)处，进入由参考标签组成的正三角形拓扑结构的辅助定位网络，开始接收读写器发出的信号，并反向散射出应答信号，读写器在模拟室内环境的4个角处接收参考标签和待测标签的应答信号。

(2)仿真利用对数正态路径损耗模型将标签到读写器的距离映射成读写器接收到的RSSI功率值，读写器接收到标签的RSSI值的同时用标签返回的ID信息，辨认出哪些是已知的参考标签，哪些是未知的待测标签。

(3)阅读器利用接收到标签的RSSI信息计算所有参考标签和待测标签在功率特征上的欧式距离，找出离待测未知标签距离最近的一个参考标签进行演习式定位，分别选取K=3，4，5，6用K临近算法对该参考标签定位并计算出定位误差，选择定位误差最小也就是最佳K值，利用该K值对待测未知标签定位。

(4)待测标签位置不变，在相同的仿真条件下重复进行100次定位，图6中的小黑点就是对待测标签100次定位的估计位置，用一个最小圆将这些估计点包容起来，其圆心就是待测点的坐标。

仿真结果如图6所示，最小包容圆定位法估计到的位置和真实位置间的误差得到了很大程度的削减，使得定位精度得到显著提高。

为了验证本文的这种最小包容圆自适应定位法的定位性能，笔者收集了100组只利用自适应K临近法的定位数据，另外收集100组在采用自适应K临近法基础上运用最小包容圆定位法的定位数据。比较这两组数据和真实待测坐标之间的距离误差后，得到两组误差数据。从图7的误差距离百分比累积曲线可以看出，同等概率下，加上最小包容圆算法的定位误差距离更小。由此可以验证，最小包容圆自适应K临近算法可以有效地提高定位性能。

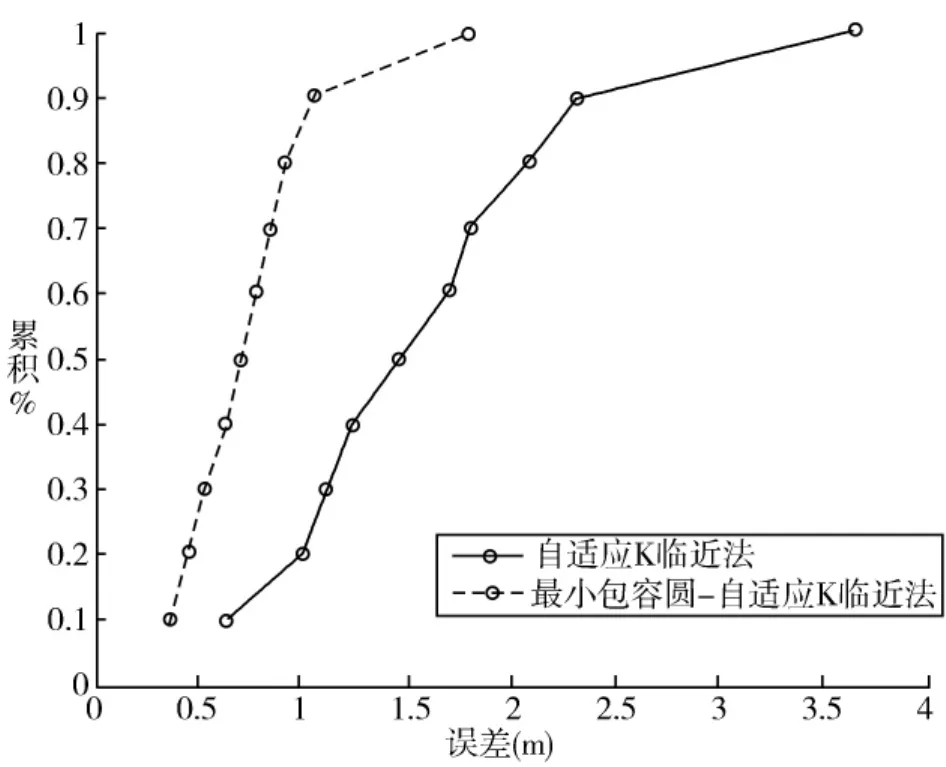
图7 误差距离的百分比累积曲线

4 结束语

本文基于对LANDMARC算法的改进，从参考标签的拓扑结构、K值的自适应选择和最小包容圆定位法三方面进行设计和仿真。仿真结果表明，本文提出的这种最小包容圆自适应定位法相对于一般基于LANDMARC算法的定位系统而言，定位性能更好，精确度更高。

[1]Ni L M，Liu Yunhao，Lau Y C，et al.LANDMARC:Indoor location sensing using active RFID[J].Wireless Networks，2004，10(6):701-710.

[2]Farhan Manzoor，Yi Huang，Karsten Menzel.Passive RFID-based indoor positioning system，an algorithmic approach[C]//IEEE International Conference on RFID-Technology and Applications.2010:112-117.

[3]Huang Yihua，Lv Shilei，Liu Zongyuan，et al.The topology analysis of reference tags of RFID indoor location system[C]//The 3rd IEEE International Conference on Digital Ecosystems and Technologies(DEST).2009:313-317.

[4]Kyuwon Han，Sung Ho Cho.Advanced LANDMARC with adaptive k-nearest algorithm for RFID location system[C]//The 2nd IEEE International Conference on Network Infrastructure and Digital Content(IC-NIDC 2010).2010:595-598.

[5]Rappaport T.Wireless Communications:Principle and Practice[M].Prentice Hall，1996:138-140.

[6]汪卫，王文平，汪嘉业.求一个包含点集所有点的最小圆的算法[J].软件学报，2000，11(9):1237-1240.

[7]Hamey L G C，Priest C.Automatic number plate recognition for Australian conditions[C]//Proceedings of Digital Image Computing Techniques and Applications.Queensland，Australia，2005:14.

[8]Wolfgang D，Wilhehn G.Interoperable 5.8GHz DSRC system as basis for European wide ETC implementation[C]//European Microwave Conference.Jerusalem，1997:139-145.

[9]刘保卫.基于RFID原理的交通目标搜索与定位技术研究[D].大连:大连理工大学，2007.

[10]傅常伦.基于车辆定位系统的数据融合及其在城市交通中的应用[D].上海:同济大学，2008.

[11]Guvenc I，Chong Chia-Chin.A survey on TOA-based wireless localization and NLOS mitigation techniques[J].IEEE Communications Surveys ＆ Tutorials 2009，11(3):107-124.

[12]Wang Zhong-hai，Zekavat S A.A novel semidistributed localization via multinode TOA—DOA fusion[J].IEEE Transactions on Vehicular Technology，2009，58(7):3426-3435.

[13]高建立.基于RFID与DSP技术的车辆定位算法研究[D].大连:大连理工大学，2008.

[14]Hata M.Empirical formula for propagation loss in land mobile radio services[J].IEEE Transactions on Vehicular Technology，1980，29(3):317-325.