基于蚁群遗传算法的属性约简
夏先智,杜新宇,郑扬飞
(华北计算技术研究所公共安全信息化事业部,北京 100083)
0 引言
属性约简是确定与给定问题最相关的属性,去除不相关、冗余的属性,从而减少数据的维度,降低相关算法的复杂度,从而提高数据处理的效率。目前,属性约简已在数据挖掘、自然语言处理和机器学习等领域中得到很多研究者的关注。
Z.Pawlak提出的粗糙集理论[1-4]为属性约简提供了理论基础。人们期望从一个知识系统中的多个约简集中找到一个属性最少且保证其正确率的最小约简,但求解最小约简已被证明是一个NP-Hard问题。
蚁群算法是模拟蚂蚁群体觅食的仿生优化算法,在求解组合优化问题的方面表现了突出的适用特征,已经成功地在大量领域获得了应用,如机器人系统、图像处理、制造系统、车辆路径系统、通信系统等领域。文献[5-8]将蚁群优化应用于属性约简问题,但均是针对蚁群算法的状态转移规则和信息素更新规则的调优,没有考虑到蚁群算法本身的缺点:蚁群需要迭代多次获取足够的信息素浓度来选择路径,因此导致算法迭代次数多,收敛慢。
本文将复制、交叉、变异等遗传算法因子引入到蚁群算法,改进蚂蚁寻解的过程,使得蚁群更快地扩算到全局问题空间,以提高算法的收敛速度和全局搜索能力。
1 相关理论
1.1 粗糙集相关概念[9-11]
定义1 假设S为待约简的知识系统,U为S中带有属性的对象集合,那么知识系统可以表示为S=(U,A,V,f)。其中A表示U中对象的属性集合,用C表示条件属性的集合,D表示决策属性的集合,则有A=C∪D,C∩D=φ。V表示属性约简后最优解的属性集合。f:U×A→V表示全部属性到最优解的属性集合的映射,且有∀x∈U,∀a∈A,f(x,a)∈Va其中Va为属性a的值域。
定义2 对于属性集合P和Q,P⊆U,Q⊆U,定义Q对P的依赖度为:
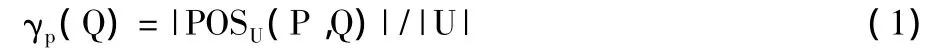
其中,|U|表示U的属性个数;POSU(P,Q)表示Q的P正区域,0≤γp(Q)≤1。依赖度反应了属性之间的相关性,γp(Q)越大,则Q对P的依赖度就越高,Q的独立度就越低,被约简的可能性就越高。
定义3 设属性集合R⊂C,∀a⊆C-R,定义a对于决策表属性D的重要度为:
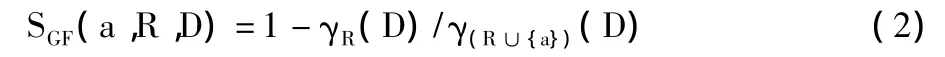
其中,γR(D),γ(R∪{a})(D)分别为决策属性D对属性集合R和R∪{a}的依赖度。在R已知的情况下,SGF(a,R,D)越大,属性a对于决策属性D就越重要。
定义4 设R为条件属性集合C的一个约简,则它必须满足条件:
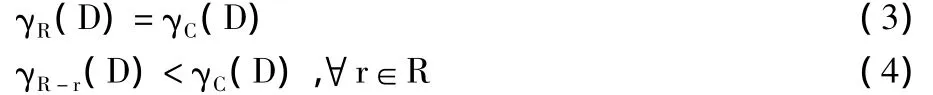
其中,γR(D)、γC(D)、γR-r(D)分别表示决策属性集合D对条件属性集合R、C、R-r的依赖度。公式(3)等价于γC-R(D)=0,表示D不依赖于被约简的属性集合C-R的任一属性。由于C的约简并不唯一,所有约简的交集,即约简R必须包含的属性集合称为属性核,记为Rcore,而具有最少属性的约简,称为最小约简,记为Rmin。
1.2 蚁群算法
蚁群算法(Ant Colony Optimization,ACO),是由Marco Dorigo于1992年在他的博士论文中提出,是一种用来在图中寻找优化路径的机率型算法,最初在求解旅行商问题取得较好的效果,是从蚂蚁协作发现食物的过程中得到的灵感。大量蚂蚁组成的群体集体行为表现出了正反馈的现象:越多的蚂蚁从同一条路径上走过,该路径积累的分泌物浓度就越大,之后的蚂蚁选择该路径的可能性就越大。蚂蚁就是通过这种分泌物的指引,判断前进的方向,找到通向食物的最短路径。在蚁群算法中,算法假设蚂蚁会在每一条它走过的路径上留下一些信息素,它也会根据路径的信息素强度来选择下一步路径,选择的概率取决于路径上信息素的强度。蚁群算法是模仿真实蚁群的正反馈原理,模拟蚂蚁的行为,从而实现寻优。
2 蚁群遗传算法求解属性约简
2.1 约简目标
根据定义4,属性约简的结果R必须满足:

而最小约简Rmin可以表示为:

在求解最小约简之前,首先要求解属性核,属性核Rcore为所有约简的交集,是每个约简不可缺少的部分,因此决策属性集D,完全依赖于Rcore的任一属性,即满足:

因为|U|为常数,本文直接比较正区域的基数大小来求解属性核,其过程如下:
(1)计算正区域 POSU(C,D)以及所有的 POSU(C -{i},D),其中 i为条件属性,i∈C;
(2)计算每一个条件属性的正区域基数差值|POSU(C,D)|- |POSU(C -{i},D)|;
(3)将上一步结果排序,选择差值为零的条件属性组成属性核Rcore。
另记B=C-Rcore表示可选条件属性集,最小约简的条件公式(5)和公式(6)可以变换为:
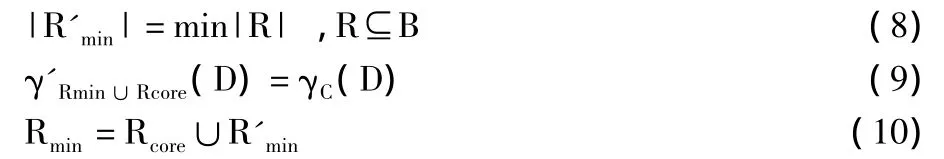
因此,属性约简问题可以定义为从可选条件属性集B中,选择满足公式(9)的属性集合,按照公式(8)求解最小约简R'min。
2.2 基本蚁群算法求解过程
基本蚁群算法模拟了蚁群协作觅食的过程。算法需要定义蚂蚁信息素的表示方式和信息素的分泌和挥发规则,确定状态转移规则(蚂蚁选择路径的方式),设置迭代停止条件。基本蚁群算法的流程过程是,算法首先按照一定规则初始化信息素和算法参数,然后开始迭代为每一只蚂蚁构造可行解。每次蚂蚁从初始节点出发,开始迭代,然后可选节点的信息素信息,根据状态转移规则选择下一个节点,直到最大迭代次数或得到可行解为止。
基本蚁群算法容易出现早熟、迭代次数过多的问题,因此引入遗传算法中复制、交叉和变异等遗传因子,改进其状态转移过程,使得信息素能够快速积累,且蚂蚁不出现集群现象。
2.3 信息素的定义和更新规则
信息素定义和更新规则是蚁群算法的基础,一个可选属性的信息素浓度决定了它被蚂蚁选择的概率。因此,信息素更新规则的目标是使蚂蚁倾向于选择最优解中包含的属性来构建可行解。
假设任意两个属性i,j之间存在一虚拟的弧段,弧段记录两端属性之间的信息素强度τij,显然,可行解属性之间的弧段实际上表示了蚂蚁在属性空间上所走的路径,而属性约简就是为了在这属性空间中找到满足公式(5)的最短路径。信息素强度τij表示当解集包含属性i时,蚂蚁选择属性j的期望。由于属性之间没有顺序关系,因此τij与τji是等价的,在求解过程中,算法只需计算τij。而算法初始时刻,属性之间的关系是未知的,因此算法初始化时,设置所有属性之间的信息素强度τij(0)=τ0。
在找到可行解后,蚂蚁会对信息素进行更新。蚂蚁已经选择的属性之间信息素信息会增加,所有属性之间的信息素随时间流逝而减少。信息素衰减只与时间有关,而与蚂蚁的行为无关。信息素的更新主要增加信息素浓度。
记Rmin1和Rmin2分别为当前迭代为止,选出的最优解和次优解。蚂蚁下次迭代应该优先在Rmin1和Rmin2区域寻找最优解。信息素更新规则将分别增强Rmin1和Rmin2中两两属性节点间的信息素浓度。这样,如果蚂蚁构造的新解中已经包含了Rmin1或Rmin2中的部分属性,那么蚂蚁应该优先选择Rmin1或Rmin2中的其它属性。信息素更新规则定义为:

其中,p(0<p<1)表示信息素存留系数,pτij(t)是信息素衰减之后剩余的信息素浓度;Δτij(t)表示第t次迭代中属性i和j之间信息素的增量,它反比于Rmin1或Rmin2中包含的属性个数。显然,最优解Rmin1中属性之间的信息素增量最多,次优解Rmin2中的属性之间的信息素增量比最优解的少。其它属性之间的信息素增加为零。
2.4 状态转移规则
状态转移规则决定了蚂蚁如何选择下一个属性来构造可行解,它直接影响了最优解的质量,也决定了算法的收敛速度和迭代次数。本文中,蚂蚁是根据赌轮算法来选择下一个属性,状态转移规则需要确定每一个属性被选择的概率。
在属性约简中,解集是属性的集合,属性顺序是无关的,下一个属性的选择只能由已经选择的属性来决定。设Rk为已选属性的集合,k为迭代次数,j为待选属性,则选择j的概率为:
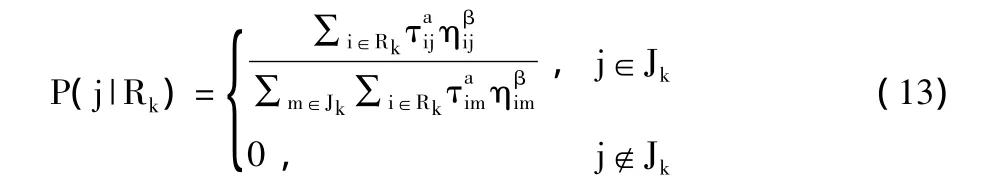
其中,集合Jk=C-Rk为第k次迭代后剩余可选条件属性;ηij表示属性j对属性i的重要性,根据定义3,则有 ηij=SGF(j,{i},D),β(β≥0)表示重要性的权重。因此可以认为是属性i对属性j的期望,表示集合 Rk对属性 j的期望。∑m∈Jk表示集合R从J中选择任一可选条件属kk性的期望之和。P(j|Rk)表示了蚂蚁在Rk为已选属性的集合情况下,从剩余可选条件属性中选择属性j的概率。
2.5 蚁群的复制、交叉和变异
蚁群算法是一种模仿了蚁群行为的算法。这种正反馈原理会导致蚂蚁在求解过程中,向同一个解聚集,从而导致算法早熟,最优解其实为局部最优、因此,本文引入复制、交叉和变异这些遗传因子来改进蚁群算法的状态转移规则,旨在解决蚁群算法局部最优、早熟、迭代次数过多的问题。
在遗传算法中,复制的目标是保留父代优质个体,因为它可能更接近全局最优解。蚁群算法中,复制的目标是保留交叉或变异操作要求保留的蚂蚁个体。
为了防止蚂蚁的聚集,通过引入交叉和变异,为蚁群增加一些“胆大”的蚂蚁,它们在当前最优解区域之外构造可行解,增加蚁群算法的全局搜索能力,避免局部最优。
交叉操作是在蚂蚁构造可行解过程中进行的,每当所有未完成可行解构造的蚂蚁选择了一个新的属性,则计算决策属性D对这些蚂蚁解集的依赖度,选出依赖度最高的2个解集,记为R1和R2,按照交叉概率pc将其进行交叉操作,交叉规则如下:
(1)首先分别从R1和R2中随机选取k个条件属性,各自构成的集合记为S1和S2,其中k大于0,小于 min(|R1|,|R2|);
(2)将S2加入到最优解R1中,然后删除重复的属性,得到解R3;
(3)同样的方法,将S1加入到次优解R2中,删除出现重复的属性,得到解R4;
(4)按照定义2计算决策属性D对解R3和R4的依赖度,如果R(R3或R4)的依赖度大于R1或R2,则创建新的蚂蚁,解集初始化为R,加入迭代。
变异操作是增加遗传算法中个体的多样性。遗传算法中,变异一般是通过调整解编码的顺序完成。但是在属性约简中,属性之间的顺序是没有意义的,因此无法更改可行解中的属性顺序来完成变异操作。因此,在本算法中,可行解的变异操作过程为:信息素奖励之后,可行解R按照变异概率pm来决定是否进行变异,如果需要变异,则从可行解中随机选择km个条件属性删除,然后复制该蚂蚁,蚂蚁进入下一次迭代。
2.6 蚁群遗传算法流程描述
(1)根据定义2,计算决策属性集合D对条件属性集合C的依赖度γC(D)。
(2)根据2.1节的算法求解核属性集合Rcore,然后根据定义2计算D对属性核的依赖度γRcore(D)。
(3)若γC(D)=γRcore(D),取Rmin=Rcore,算法终止,否则转步骤(4),进行蚁群遗传算法求解属性约简。
(4)蚁群算法进行初始化,选取起始蚂蚁数量为|C|,初始化所有属性之间的信息素为τ0,计算任意两属性之间的重要度ηij,并设定最大迭代次数Tmax,当前迭代次数t=0。
(5)开始第t次迭代,蚂蚁开始构造可行解,设蚂蚁的解集合为Ri,i为蚂蚁编号,将Ri初始化为属性核Rcore。
(6)判断Ri是否为可行解,若为可行解,保留该解,并标记蚂蚁个体为死亡状态,转步骤(8),若不为可行解转步骤(7)。
(7)根据状态转移规则计算Ri选择C–Ri中每一个属性的概率,并根据赌轮算法,选择下一个属性。计算D对每一只活着的蚂蚁的解集Ri当前的依赖度,选择依赖度最高的2只蚂蚁,复制,然后按照交叉概率pc进行交叉操作。返回步骤(6)。
(8)当所有蚂蚁完成可行解的构造时,按照变异概率pm对可行解进行变异,然后复制变异成功的蚂蚁,下一次迭代时,蚂蚁继续构造可行解。
(9)从所有可行解中选出最优解Rmin1和次优解Rmin2,根据信息素更新规则,对属性之间的信息素进行更新。
(10)置 t=t+1,若 t< Tmax,则返回步骤(5),否则取Rmin=Rmin1,终止算法。
3 实验结果与分析
为了验证算法的有效性,使用Python语言实现了文献[12]的基本蚁群算法和本文的蚁群遗传算法,并选择了和文献[12]相同的决策表对算法进行测试,决策表数据可以从加州大学提供的机器学习数据库(UCI Machine Learning Repository)[13]下载到。
其中基本蚁群算法基本参数与文献[12]一致,即 α =1.0、β =0.1、Nant=|C|、Tmax=250、τ0=20,遗传操作中的参数设定为,交叉概率pc=0.667,变异概率 pm=0.015。
随后重复对每个决策表进行多次测试,记录每次获得最优解的迭代次数和最小约简结果。如表1所示。
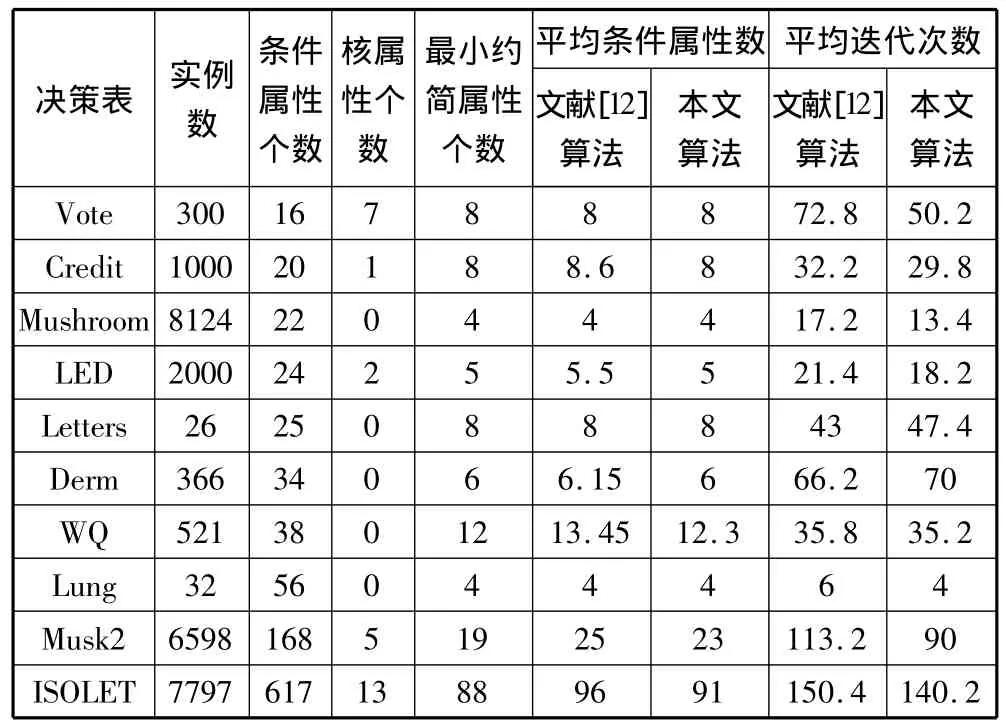
表1 蚁群遗传和普通蚁群算法约简结果对比
本文算法和文献[12]算法的主要差别在于,在状态转移之后,蚂蚁需要复制和交叉,在蚂蚁构造可行解后,需要对可行解进行变异,通过遗传操作,扩大蚂蚁的搜索空间,优化蚁群算法。
从表1的统计结果看,对于大部分决策表,本文算法获得的结果和迭代次数都优于文献[12]。也有少部分表结果并不理想,如Letters和Derm,但其结果也比较接近。因此,可以说本文引入的遗传算法因子对蚁群算法改进是有效的,能够提高蚁群优化处理属性约简问题的效果。
4 结束语
本文将遗传算法中的遗传因子引入到蚁群优化,应用于决策表属性约简的问题。通过复制、交叉、变异遗传因子,保留优质解,同时提高了蚂蚁的全局搜索能力。最后在多个决策表上的测试表明,本文设计的算法提高优化了蚁群算法全局搜索能力,减少了迭代次数,能够有效地解决属性约简问题。
[1]汪杭军,张广群,方陆明.粗糙集属性约简算法的实现与应用[J].计算机工程与设计,2007,28(4):777-779.
[2]于冰,阎保平.关于粗糙集属性约简的进化算法研究和应用[J].微电子学与计算机,2005,22(3):189-194.
[3]瞿彬彬,卢炎生.基于粗糙集的快速属性约简算法研究[J].计算机工程,2007,33(11):7-9.
[4]瞿彬彬,卢炎生.基于粗糙集的属性约简算法研究[J].华中科技大学学报:自然科学版,2005,33(8):30-33.
[5]袁浩.基于量子蚁群算法的粗糙集属性约简方法[J].计算机工程与科学,2010,32(5):82-84.
[6]于洪,杨大春.基于蚁群优化的多个属性约简的求解方法[J].模式识别与人工智能,2011,24(2):176-184.
[7]姚跃华,洪杉.基于自适应蚁群算法的粗糙集属性约简[J].计算机工程,2011,37(3):198-200.
[8]任志刚,冯祖仁,柯良军.蚁群优化属性约简算法[J].西安交通大学学报,2008,42(4):440-444.
[9]Pawlak Z.Rough sets and data analysis[C]//Proceedings of the 1996 Asian Fuzzy Systems Symposium.1996.
[10]Pawlak Z.Theorize with data using rough sets[C]//Proceedings of the 26th Annual International Computer Software and Applications Conference.2002:1125-1128
[11]Pawlak Z.Why rough sets?[C]//Proceedings of the 5th IEEE International Conference on Fuzzy Systems.1996:738-743.
[12]Jensen R,Shen Q.Finding rough set reducts with ant colony optimization[C]//Proceeding of the 2003 UK Workshop on Computational Intelligence.2003:15-22.
[13]UCI.UCI Machine Learning Repository[EB/OL].http://archive.ics.uci.edu/ml/,2012-08-15.
[14]Liu Hongjie,Feng Boqin ,Li Wei.An approach to minimum attribute reduction[C]//IEEE International Conference on Automation and Logistics.2008:1589-1593.
[15]Xu Zhangyan,Gu Dongyuan,Yang Bo.Attribute reduction algorithm based on genetic algorithm[C]//Proceeding of the 2nd International Conference on Intelligent Computation Technology and Automation.2009:169-172.

