基于对称性计算N皇后问题的非递归算法

孙国伟，买阿丽

(1.运城学院应用数学系，山西 运城 044000;2.广州大学数学与信息科学学院，广东 广州 510006)

0 引言

N皇后问题[1-3]是一个古老而著名的问题，该问题是在N×N的国际象棋棋盘上，放置N个皇后，使任何两个皇后都不能相互攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上。N皇后问题是由八皇后问题演化而来的。八皇后问题于1848年由国际象棋棋手 Max Bazzel提出[1]。

N皇后问题是一个NP难问题，近年来已经成为计算机应用领域内的一个经典问题。学者们针对此问题提出了许多解决方法。Jordan Bell等人总结比较了2007年以前提出的各种解法[1]。目前对N皇后问题的计算主要有两方面的研究，一方面是设计高效的算法去计算问题的所有解，如回溯法[2-4]、并行算法[5]、位运算方法[6-8];另一方面是快速寻找此问题的一部分解[9-12]。

本文使用回溯法寻找N皇后问题的全部解。回溯算法可以用递归方法来实现，也可以用非递归方法来实现。用递归的方法来解决回溯问题时，思路很清晰，但速度较慢;非递归方法相对速度快，但是程序的逻辑结构却很复杂。不论用哪种方法实现，当N较大时还没有一种高效的算法。

为了提高算法的计算效率，需要研究N皇后问题解的性质，利用性质缩小搜索空间。文献[5]和文献[12]均研究了解的旋转性质。文献[5]利用旋转性质实现了N皇后解的快速计数。文献[12]首先考虑计算出N皇后的全部解，之后再利用旋转性质计算基础解。文献[8]利用回溯法，基于位运算计算N皇后问题，但是程序复杂，且仍在整个解空间中搜索。本文提出N皇后问题解的4个对称性质，并利用性质缩小搜索空间，给出利用对称性计算N皇后全部解的一个非递归算法。

1 N皇后问题算法设计

N皇后问题的解空间可以描述为:

其中，Q=(a1，a2，…，aN)表示在棋盘的第 i行第 ai列放置一个皇后，i=1，2，…，N。因此可用自然数集合{1，2，…，N}的排列树来描述解空间，如图1所示。

图1 4皇后解空间的排列树

图1为4皇后解空间，其中每一个节点旁边的编号表示棋盘的列号，第i层节点表示在棋盘第i行可以放置的与前i－1行皇后满足行列不冲突的列，i=1，2，3，4。

根据对角线不冲突的约束知，若Q=(a1，a2，…，aN)∈S，则当且仅当对任意 i≠j，有:

则Q为N皇后一个解。

可以利用树的深度优先遍历来实现回溯法，并在计算过程中利用式(1)进行剪枝，计算N皇后问题的解。

假设在棋盘的第i行第ai列放置一个皇后之后，则可以利用式(1)计算出当这个皇后放置以后第i+1行可以放置皇后的列，从而在每次回溯时，只在每一行可以放置皇后的列中继续进行搜索，避免对角线不冲突约束的重复判断，提高计算效率[8]。

算法1 N皇后非递归算法。

P1如果N==1，输出“1皇后有一个解”，算法结束，否则执行P2至P4。

P2初始化栈S1。栈长为N+1。即将整数1，2，…，N形成含有N个元素的队列，每个队列元素包含两项，数字域和标志域。初始化时所有元素的标志域均置为0，并依据整数递增顺序进入队列。再将此队列压入栈S1。

P3初始化栈S2为空，栈长为N。

P4当栈S2不空或栈S1栈底队列中还有元素的标志位为0时，循环执行4.1至4.3。

4.1 当栈S2中元素个数小于N，且栈S1栈顶队列中存在标志位为0的元素时，循环执行4.1.1至4.1.4。

4.1.1 弹出S1的栈顶元素，记此队列为L1;

4.1.2 记队列L1的队头元素之后第一个标志域为0的元素为h，并将h所对应的数字域的值a压入栈S2;再将L1中除a之外的数字，形成一个队列L2，并将L2中满足式(1)条件的元素标志位置为1，其余标志位置为0，并依据整数递增顺序进入队列;

4.1.3 将队列L1中h的标志位改为1，并将队头移至h，再将L1压入栈S1;

4.1.4 将 L2压入栈 S1。

4.2 如果栈S2中元素个数等于 N，执行4.2.1至 4.2.2。

4.2.1 从S2的栈底开始，从下往上依次输出栈中元素产生一个新解。解的个数加1。

4.2.2 栈S2栈顶出栈。

4.3 当S2不空且S1栈顶队列中元素标志位全为1 时，循环执行4.3.1 至 4.3.2。

4.3.1 弹出S1栈顶元素;

4.3.2 弹出S2栈顶元素。

2 N皇后算法分析

图2为4皇后问题排列树的剪枝示例图。图2中粗线表示4 皇后问题的两个解:2，4，1，3 和3，1，4，2;虚线表示被剪去的树枝;有标号的节点表示进入过栈S1的节点，实线上有标号的点表示进入过栈S2的节点。

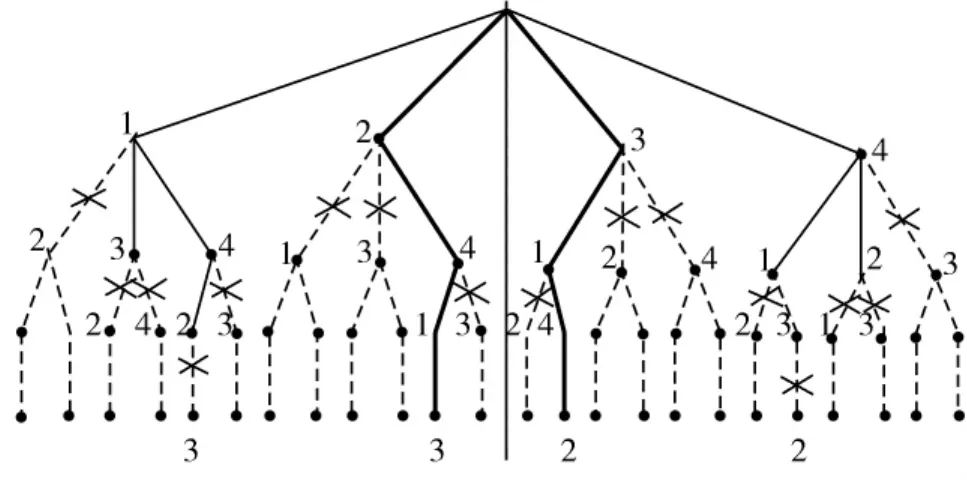
图2 4皇后问题的解及排列树剪枝示例

使用栈和队列实现非递归组合生成算法，栈和队列均采用顺序存储方式[13-14]。栈S1需要2·(n+1)个空间，栈S2需要n个空间，因此空间复杂度为O(3n)。时间复杂度是一个需要继续研究的问题。

3 N皇后解的性质

N皇后问题的部分解可以由其他解经对称和旋转变换得到。当以{1，2，…，N}的全排列树表示N皇后问题的解空间时，每个解对应于一个全排列Q=(a1，a2，…，aN)，此时有如下4 个对称性质。

性质1 如果Q=(a1，a2，…，aN)为N皇后问题的一个解，则它关于棋盘左右对称的解为Q1=(b1，b2，…，bN)，其中 bi=N+1 － ai。例如解 1，3，5，2，4关于棋盘左右对称的解为 5，3，1，4，2。

性质2 如果Q=(a1，a2，…，aN)为N皇后问题的一个解，则它关于棋盘次对角线对称的解为Q2=(c1，c2，…，cN)，其中 Q2的第 N+1 － ai个值为 N+1－i，即 cN+1－ai=N+1 －i。例如解 1，3，5，2，4 关于棋盘次对角线对称的解为 3，1，4，2，5。

性质3 如果Q=(a1，a2，…，aN)为N皇后问题的一个解，则它关于棋盘上下对称的解为Q3=(d1，d2，…，dN)，其中 Q3的第 i个值为 aN+1－i，即 di=aN+1－i;例如解1，3，5，2，4 关于棋盘上下对称的解为4，2，5，3，1。

性质4 如果Q=(a1，a2，…，aN)为N皇后问题的一个解，则它关于棋盘主对角线对称的解为Q4=(e1，e2，…，eN)，其中 Q4的第 ai个值为 i，即 eai=i。例如解1，3，5，2，4关于棋盘主对角线对称的解为1，4，2，5，3。

容易验证性质1至4与文献[12]中的4个三维旋转性质等价，但叙述更简单更易于算法实现。表1为算法1计算出的5皇后问题的解。其第一行从左到右，紧接着在第二行从右到左为解的产生顺序。同一列的解具有左右对称性。

表1 5皇后问题的解

图3 为5 皇后解 1，3，5，2，4 和2，5，3，1，4 对称示例。图3中每5×5的方格表示一个棋盘，方格中的数字表示在对应行中的相应列放置皇后。有线相连的方格表示两个解相互对称，两个方格之间连线上的文字表示对称的类型。粗虚线左侧为解1，3，5，2，4的左右、上下、主对角线和次对角线的对称解。粗虚线右侧表示解 2，5，3，1，4 的左右、上下、主对角线和次对角线的对称解均为解 4，1，3，5，2。

图3 5皇后解1，3，5，2，4 和2，5，3，1，4 对称示例

图4为5皇后全部10个解对称情况。图4中每个顶点表示一个解，有边相连的顶点表示两个解相互对称，边上的文字表示对称的类型。

图4 5皇后全部10个解对称情况

4 N皇后优化算法

可以结合算法1和性质1描述的左右对称性，得到一个优化算法。从图2可以看出粗虚线左侧的解正好和右侧的解左右对称。因此只需在排列树的左侧搜索满足条件的解，再利用对称性计算右侧的解。在栈S1和S2采用顺序存储，且元素以递增顺序入队时，优化的N皇后非递归算法，只需在算法1的基础上做如下修改。

(1)在算法1 的第4.1.2 和4.1.3 之间增加一个判定条件，“如果n为偶数且S2[1]大于n/2，或者n为奇数且 S2[1]大于1+n/2 且 S2[2]大于 n/2，算法结束。”其中，S2[1]表示为栈S2栈底元素。

(2)修改4.2.1为“从 S2的栈底开始，从下往上依次输出栈中元素产生一个新解;同时依据左右对称性产生另一个解。解的个数加2。”

表2 算法1、优化后的算法及文献[8]的运行时间和解的个数

从图1知4皇后解空间的排列树共有64个节点，从图2知在计算4皇后解时只访问了左半树中的16个节点。搜索节点为解空间的25%，性能的提升还是比较明显的。为了与同样采用回溯法，但利用位运算操作，基于Erlang语言平台计算N皇后问题解的文献[8]进行比较，同样在 Core 2、2.94 GHz、2 GB内存的电脑上进行试验。使用C++程序设计语言，实现了算法1和优化的N皇后非递归算法，计算了11～18皇后问题的解。算法1、利用对称性优化后的算法及文献[8]的运行时间和解的个数如表2所示。

5 结束语

针对非递归方法相对速度快，但是程序的逻辑结构却很复杂的问题，笔者采用栈和队列实现了利用回溯法计算N皇后问题的一种新的非递归算法，该算法逻辑清晰，并在搜索过程中进行剪枝，使得每次回溯后只需搜索每一行可以放置皇后的位置，从而提高了算法的效率。同时如理论分析及表2所示，利用性质1能极大地提高N皇后问题的计算效率，相比文献[8]计算效率也有一定的提高。但是，从图3和图4可以看出，N皇后问题的解相互之间具有较复杂的对称性。如何结合其余3个性质进一步缩小搜索空间提高计算效率是一个需要继续研究的问题。

[1]Jordan Bell，Brett Stevens.A survey of known results and research areas for N-Queens[J].Discrete Mathematics，2009，309(1):1-31.

[2]Anany Levitin.算法设计与分析基础(第2版)[M].潘彦译.北京:清华大学出版社，2007:315-316.

[3]王晓东.计算机算法设计与分析[M].北京:电子工业出版社，2001:132-135.

[4]Solomon W Golomb，Leonard D Baumert.Backtrack programming[J].Journal of the ACM，1965，12(4):516-524.

[5]韩宇南，吕英华，黄小红.并行改进回溯算法实现N皇后问题的快速计数[J].计算机工程与应用，2006，42(36):1-3.

[6]Martin Richards.Backtracking Algorithms in MCPL Using Bit Patterns and Recursion[R].UCAM-CL-TR-433.United Kingdom:University of Cambridge，Computer Laboratory，1997.

[7]潘大志，杜勇，谭代伦，等.位运算在N皇后问题中的应用[J].计算机工程与应用，2009，45(32):61-62.

[8]向宏，孙黎明，桑军.改进的基于Erlang的N皇后问题算法[J].计算机工程与应用，2012，48(10):64-67.

[9]Jacek Mandziuk，Bohdan Macukow.A neural network designed to solve the N-queens problem[J].Biological Cybernetics，1992，66(4):375-379.

[10]Wei Zhang，Zheng Tang.A new algorithm using hopfield neural network with CHN for N-queens problem[J].International Journal of Computer Science and Network Security，2009，9(4):36-41.

[11]Sosic Rok，Gu Jun.A polynomial time algorithm for the NQueens problem[J].SIGART Bulletin，1990，1(3):7-11.

[12]黄达峰.N皇后问题解的构造及等价性分析[D].广州:中山大学，2008.

[13]严蔚敏，吴伟民.数据结构(C语言版)[M].北京:清华大学出版社，2006:44-65.

[14]Larry Nyhoff.数据结构与算法分析—C++语言描述(第2版)[M].黄达明译.北京:清华大学出版社，2006:280-309，345-361.