基于改进蚁群算法的无人机航迹规划

韩 攀,陈 谋,陈哨东,刘 敏

(1.南京航空航天大学 自动化学院,南京 210016； 2.洛阳光电设备研究所 光电控制技术重点实验室,河南 洛阳 471009)

0 引 言

随着科技发展和社会进步,现代无人机运用的领域和范围越来越广,执行的任务也更加复杂和多样化。好的航迹可降低任务风险或成本,航迹优化的价值也随之变高。航迹规划作为无人机自主飞行控制研究的重要内容之一,一直都是人们研究的热点,随之兴起的算法也是层出不穷。如果按实时性分类,可分为离线航迹规划和在线航迹规划[1]。离线航迹规划一般是在无人机放飞前加载已规划好的飞行航线,在飞行的过程中不再改变飞行航线,对航迹规划的实时性要求不高； 在线航迹规划是指无人机在飞行的过程中根据需要动态修改飞行航线,对实时性要求较高。文献[1]对在线航迹规划的相关问题进行了研究,研究了当前常用的在线航迹规划方法,阐述了在线航迹规划的通用结构框架以及面临的关键问题。但总体来说,在线航迹规划是在离线航迹规划基础上进行的。因此,笔者主要研究离线航迹规划技术并提高其全局优化能力。

航迹规划算法如果按照规划决策的计算方法分类,可分为最优式和启发式算法。最优式算法包括穷举法、动态规划和数学规划等[2]。启发式算法则包括启发式搜索、神经网络、模拟退火和遗传算法等[3]。两者的根本区别在于,最优式算法的计算时间随系统规模的变大而呈现爆炸式增长。如果按照几何学的观点分类,可将其分为基于栅格的算法和基于图形的算法。如文献[4]运用Voronoi图对航迹规划问题进行建模,通过Voronoi图对规划空间进行分区,然后根据约束条件求解航迹规划问题。两者各有所长,一般来说,后者的处理结果比较准确,但需要相对较长的收敛时间； 前者可在实时要求的条件下收敛,但对一些约束条件难以处理。

由于航迹规划问题是个多约束条件的组合优化问题,各约束条件之间存在耦合,目前常用的算法在航迹规划的运用中各有所长,但也普遍存在着一些缺点。如传统的数学计算方法结果精确,但对于模型要求严格,且随着问题规模的增大,计算时间和所需的存储空间也迅速变大； 新兴的智能计算方法计算速度快,对模型要求不高,但算法易停滞和陷入局部最小值。所以,实际应用中一般会根据具体的问题改进算法[4-7],如文献[5]结合了蚁群算法和遗传算法,利用遗传算法的变异特性弥补蚁群算法运行后期收敛慢的缺陷； 文献[6]结合了知识库和蚁群算法,通过动态更新知识库调整算法参数,从而使算法的动态性增强。

蚁群算法最早由Dorigo等[8]作为一种多Agent的方法,很好地解决了一些复杂的组合优化问题。目前已经有很多种基于蚁群算法或其改进算法应用于各种不同的离散优化问题,这些研究已经涵盖了路径规划,顺序订货问题以及网络中的路由通信问题等[8-12]。蚁群算法以其良好的动态性、鲁棒性以及全局的并行计算能力而被广泛应用于各领域。笔者以蚁群算法为基础,求解航迹规划问题,对于蚁群算法在航迹规划中的应用做了分析和研究。针对基本蚁群算法在收敛后期易陷入局部最优的缺点,通过引入去交叉禁忌搜索策略改进算法,提高了算法的全局优化能力,进而提高无人机的航迹规划效果。

1 问题描述

无人机执行任务多种多样,每个问题的约束条件也不完全相同。如何评价一条航迹的优劣,是解决无人机航迹规划问题的前提。不妨先设定按某一航迹执行任务的航迹总代价为

C=∑Ci

(1)

其中Ci为每段航迹执行任务的航迹代价,简称为任务段代价。任务段代价受任务段的约束条件控制,例如飞行距离、飞行时间和油耗等。设约束集合为Ri={Ri1,Ri2,Ri3,…},按任务段约束条件,Ci可看作是对Ri的加权求和

Ci=∑RijWij

(2)

其中Rij为当前任务段的约束,Wij为该约束对应的权值。假设Ci可求出,并且Ci为无量纲数值,则每个任务段的代价可看做一个无量纲的确定值。每个任务段之间的代价Ci用任务段的代价Li表示

Li=liwi

(3)

其中li是航路点之间的欧式距离,wi为权值。在一般情况下无人机执行侦察和巡逻任务都是在固定高度定速飞行,只有在起飞和着陆阶段才有高度和速度的变化,因而在计算任务段代价时可以忽略高度的影响。笔者设定航路点集合为V={(Vx1,Vy1),(Vx2,Vy2),…,(Vxm,Vym)},m为航路点的个数。假设每个任务段的主要约束条件为飞行距离、飞行时间和油耗,当无人机速度一定时,飞行时间和油耗与飞行距离成正比,因此,在计算任务段的代价时可只用飞行距离表示,式(3)中wi为一个常数。为便于计算,假定wi=1。此时无人机的航迹规划问题就是确定一条通过所有航路点的最短距离的闭合航路,这与旅行商问题的描述是一致的,因此无人机航迹规划问题可以转化为TSP(Travelling Salesman Problem)旅行商问题。

2 基于改进蚁群算法的无人机航迹规划

2.1 蚁群优化算法

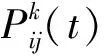
(4)

其中ηij为启发因子,表示从城市i到j的期望程度,一般是城市距离dij的倒数,可写为

ηij=1/dij

(5)

信息素更新公式为

(6)

其中

(7)

基本蚁群算法的参数主要有4个,其中α是表征信息素重要程度的参数,β是表征启发式因子重要程度的参数,ρ是信息素蒸发系数,Q是信息素增加强度系数。

2.2 基于蚁群算法的航迹规划

大多数情况下,无人机执行任务时飞行的航迹都是从起点出发到各个航路点完成任务再返回起点的过程。笔者的航迹规划也是以此为前提,假设无人机飞行的航路点已确定,无人机到达各航路点无时间约束,不考虑垂直方向的运动。这样航迹规划问题就可转化为TSP问题,在利用蚁群算法规划航路时,只需要将求解TSP问题时的城市坐标改为航路点坐标即可。求解TSP问题时,基本蚁群算法完整的伪代码如下[2,3]。

Step1 初始化,将蚂蚁随机分布到城市中,将蚂蚁所在的城市添加到各自的禁忌列表中。

Step2 设定结束条件,不满足结束条件,执行Step3、Step4循环。

Step3 对蚂蚁k,1≤k≤m,进行如下操作：

if (本次循环结束时能到达下一个城市i)

抵达下一个城市i；

else

记录本次循环路径。

Step4 更新路径上的信息素。

Step5 输出结果。

Step6 程序结束。

下面是运用基本蚁群算法对4个航路点的求解结果,设定4个航路点的坐标如表1所示,运用Matlab编程进行仿真,得到航迹规划的结果如图1所示。

表1 航路点坐标数据

图1是一个简单的航迹规划问题,有4个航路点,显然图1b是最优解。当迭代次数减少时,可能会出现图1a所示的结果,其他和图1a类似的几条路径这里就不列出了。

a 航迹规划图1 b 航迹规划图2

基本蚁群算法和其他组合优化算法一样,存在会陷入局部最优解的现象。针对这一现象研究学者们也尝试对基本的蚁群算法进行多方面改进。改进的思路主要有两种：1)修改与算法相关的因子,使算法与问题的相关性增强,如天才蚁群算法(EAS:Elitist Ant System)[13,14]、排序蚂蚁系统(Rank-Based Ant System)[15]； 2)与其他算法相结合,融合各算法的优点,如与遗传算法结合[5],利用遗传算法的变异特性弥补蚁群算法运行后期收敛慢的缺陷。文献[3]中对在基本蚁群算法中引入去交叉策略的改进做了分析,从这点出发对这种改进的具体实现做了研究。

2.3 改进蚁群算法

为比较图1a和图1b两条路径的优劣,把图1中两条路径放到一起并标识路径端点(见图2)。

通过比较,可发现实线所示的路径(图1a上的路径)中AB段与CD段相互交叉,由三角形的定义知

(8)

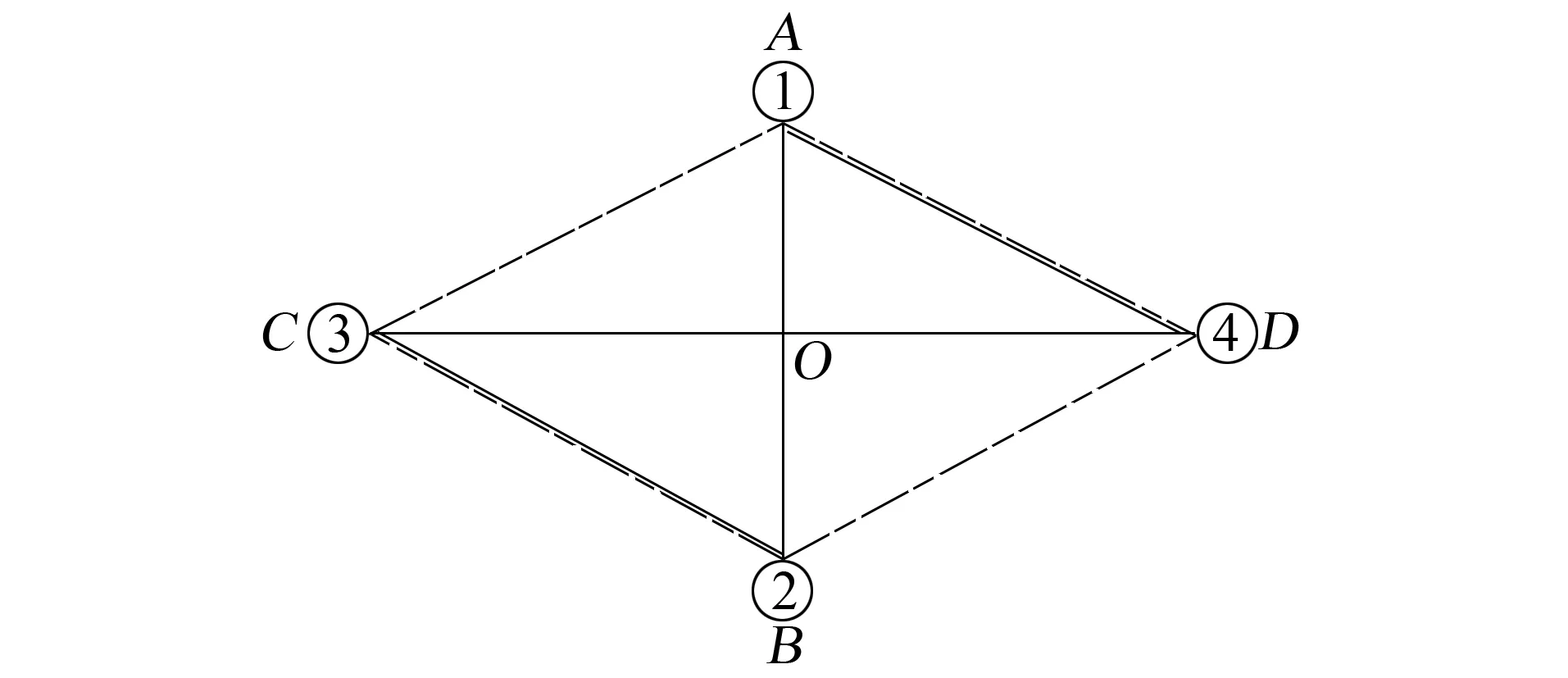
图2 路径示意图

显然|AB|与|CD|的距离大于|AC|与|BD|的距离,由此可推出图2中实线所示的路径比虚线路径长。同时可推出只要路径有交叉点,就一定有一条更优的路径存在。由此得出如下两点结论：

结论1 如果优化的路径中存在相互交叉的路径,则这条路径一定不是最优的；

结论2 如果存在一条路径使除该路径两端点以外的其他任务点,在路径规划中不得不与之交叉,则该路径一定不是最优路径里的路径。

简单的蚂蚁之所以可解决复杂的问题,是因为大量简单规则的涌现,也是团体智能的体现。任何一种改进方式,必须遵循这些简单的规则或是这些简单规则的结合与派生。人工蚁群算法中的蚂蚁和自然界真实的蚂蚁主要区别有:1)人工蚂蚁记忆能力更强,在一次循环中不会重复走过的路； 2)人工蚂蚁比较“聪明”,可以思考问题,有学习能力。如果蚂蚁能懂上面的结论,则在路径选择的过程中就能更快地找到想要的路径[4]。

针对上面的改进规则,改进思路主要如下。

1)在Step1中初始化一个启发因子,启发因子代表从城市i到j的期望程度,如果从城市i到城市j满足结论2的条件,则将这个启发因子设为零,假设蚂蚁先到达城市i,则它选择下一个城市是j的概率就是零。

2)结合结论1和结论2,在Step3中的if判断语句下增加如下代码：

if(当前到达城市i的路径不和最近走过的p条路径相交)

抵达下一个城市i； (p≤禁忌列表中的路径条数)

else

找出相交的路径,重置禁忌列表,使路径不相交。

对于1)来说,对给定的一组城市数据,要找到所有的满足结论2的路径,是个比较复杂的问题,但对一些特定的点来说,比较容易找到。改进思路是分区域地找这一类直线,显然外围点更容易产生这些直线。第1种方法,利用程序自己寻找,将外围点分类,然后用结论2进行判断； 第2种方法,可以通过程序人为地引导或设定。

对于2)实现相对容易,判断线段相交的方式有多种,重置禁忌列表的过程类似于遗传算法里的变异,而且这里的变异是向好的方向变异。假设p值代表蚂蚁的思考能力,p值越大,则同一次得到的路径趋于更优,但蚂蚁思考的时间会相应变长,这里可以根据具体的问题去调整。并且根据p值的不同,能进一步改进算法,因为变异后可能会发现新的满足结论1的路径,即变异后的路径可能与之前的路径相交,这时可以进行再次的变异,得到更优的路径。

以前面4个航路点的路径规划为例,假设在某次迭代过程中第m只蚂蚁从A点出发到达C点后禁忌列表如图3a所示,路径如图4a所示,蚂蚁要选择的下一个城市是D点,路径用虚线表示,运用改进算法判断,这时路径CD与AB相交,满足结论1的条件。下一步重置禁忌列表,重置后禁忌列表如图3b所示,路径如图4b所示。重置的规则是：假设当前路径和前面禁忌列表中的某条路径相交,则在禁忌列表中将当前路径的起始点和相交路径的结束点位置互换。如上例中当前路径为CD,相交路径为AB,在禁忌列表中将当前路径起始点C和相交路径的结束点B交换位置如图3b所示。

a 初始禁忌列表 b 修改后的禁忌列表

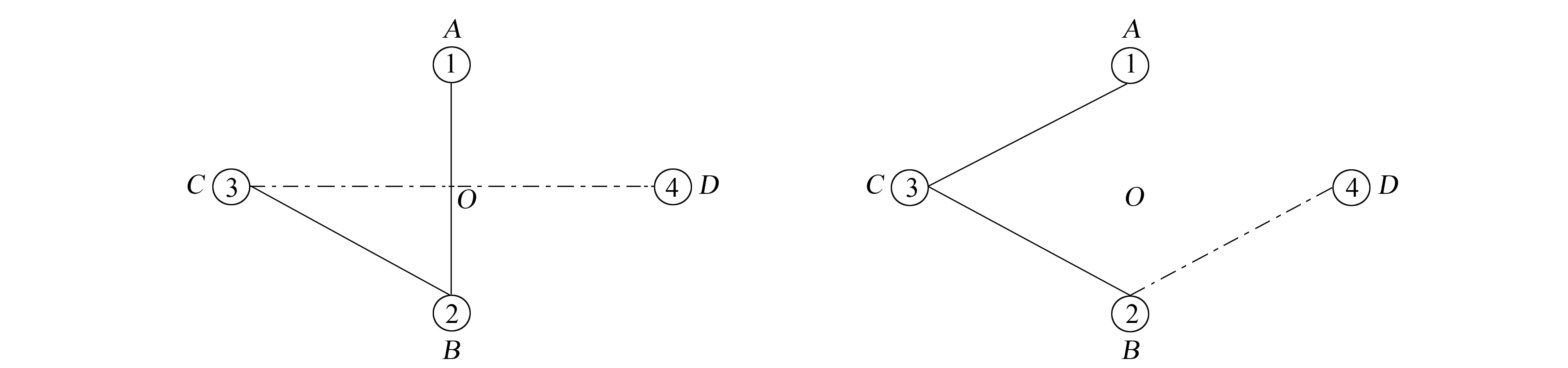
a 初始路径 b 修改后的路径

图4是一个简单的示意图,描述了重置禁忌列表变化的过程,可以看到这种改进可以增加一次迭代的优化能力,并且这种路径的改变是一种突变,类似于遗传算法里的基因变异,在一定程度上增强了算法跳出局部最优解的能力。蚁群算法是基于正反馈的算法,在算法后期解空间里路径上的信息素远远大于非解空间里路径上的信息素,一旦算法陷入局部最优解,难以再跳出来。在仿真的过程中发现这种改进可以在算法后期加入,这样在减少运行时间的同时,改进算法依旧具有一定的跳出局部最优解的能力,可以根据具体的问题去设置参数。

3 仿真测试

以chn31城市为例,设其中每个城市的坐标是无人机必经的航路点。用Matlab7.0编程对设计的算法进行了仿真测试并和基本蚁群算法做了比较。仿真硬件环境：CPU为Inter Core2 Duo 1.83 GHz,内存为2 GByte。仿真参数选取如表2所示,仿真结果如图5所示。

表2 蚁群算法参数

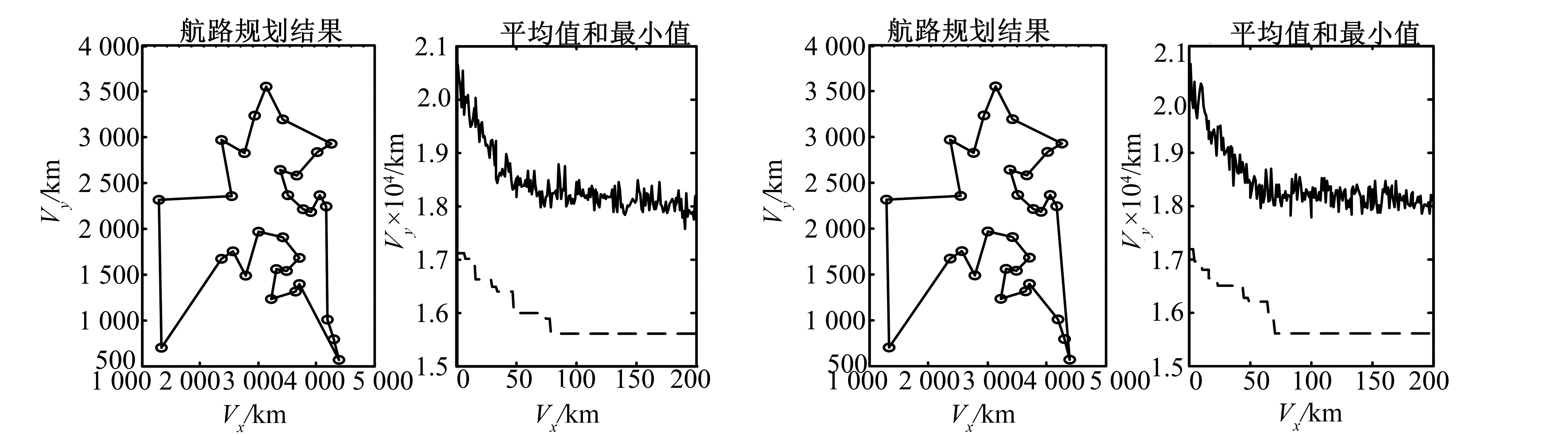
a 改进蚁群算法计算结果 b 基本蚁群算法计算结果

图5a是改进后的算法航迹规划结果图,图5b是基本蚁群算法的航迹规划结果图。图5中的左边黑色圈圈代表航路点,黑色实线是规划的航路； 右边黑色实线表示每次循环的平均值,黑色虚线表示每次循环的最优值。结果表明,蚁群算法可以运用于航迹规划和航迹寻优。仿真分析中已知的chn31最优解是15 377,迭代到200次时基本蚁群算法最优解是15 602,改进的算法是15 599,这已经接近最优解。实际上在迭代超过200次后结果已经很接近最优解了,后面曲线也比较平滑。所以,取前100次迭代的图像进行了对比。由图5可看出,改进后的算法在前期收敛速度比基本算法快,并且整体平均值较好,与前面分析的结果一致。

为进一步证实去交叉策略的有效性,笔者用几组不同城市坐标作为航路点进行仿真分析,测试结果如表3所示。

表3 不同城市坐标测试结果

通过表3可发现在有限的迭代次数中,改进后的算法可较早地搜寻到更优的解。

4 结 语

笔者对蚁群算法在无人机航迹规划中的应用进行了研究,针对蚁群算法在收敛后期易陷入局部最优的缺点,通过引入去交叉禁忌搜索策略来改进算法以提高无人机的航迹规划效果。对引入去交叉策略的蚁群算法做了仿真分析,通过仿真测试,证明了该改进增强了算法的全局优化能力,并能在航迹规划中运用和实现。通过建模和仿真测试,证明了蚁群算法应用于航迹规划是可行的。

参考文献：

[1] 胡中华,赵敏.无人飞行器在线航迹规划技术研究[J].航天电子对抗,2010,26(4):11-15.

HU Zhong-hua,ZHAO Min.Research of Real Time Route Planning for UAV[J].Aerospace Electronic Warfare,2010,26(4):11-15.

[2]左洪浩.蚁群优化算法及其应用研究[D].合肥：中国科学技术大学合肥智能机械研究所,2006.

ZUO Hong-hao.Research on the Ant Colony Optimization Algorithm and Its Applications[D].Hefei：Institute of Intelligent Machines,University of Science and Technology of China,2006.

[3]段海滨.蚁群算法原理及其应用[M].北京:科学出版社,2005.

DUAN Hai-bin.Ant Colony Algorithm Theory and Applications[M].Beijing:Science Press,2005.

[4]何艳萍,张安,刘海燕.基于Voronoi图与蚁群算法的UCAV航路规划[J].电光与控制,2009,16(11):22-24.

HE Yan-ping,ZHANG An,LIU Hai-yan.Path Planning for UCAV Based on Voronoi Diagram and Ant Colony Optimization[J].Electronics Optics &Control,2009,16(11):22-24.

[5]吴庆洪,张纪会,徐心和.具有变异特性的蚁群算法[J].计算机研究与发展,1999,36(10):1240-1245.

WU Qing-hong,ZHANG Ji-hui,XU Xin-he.An Ant Colony Algorithm with Mutation Features[J].Journal of Computer Research and Development,1999,36(10):1240-1245.

[6]孙勇,李妮,龚光红,等.基于知识库的动态蚁群算法[J].北京工业大学学报,2012,38(3):374-379.

SUN Yong,LI Ni,GONG Guang-hong,et al.Dynamic Ant Colony Algorithm Based on Knowledge Base[J].Journal of Beijing University of Technology,2012,38(3):374-379.

[7]胡中华,赵敏,刘世豪,等.基于自适应蚁群算法的无人飞行器航迹规划[J].计算机集成制造系统,2012,18(3):560-565.

HU Zhong-hua,ZHAO Min,LIU Shi-hao,et al.Unmanned Aerial Vehicle Flight Path Planning Based on Adaptive Ant Colony Optimization Algorithm[J].Computer Integrated Manufacturing Systems,2012,18(3):560-565.

[8]DORIGO M,MANIEZZO V,COLORNI A.Positive Feedback as a Search Strategy[R].Milan,Italy:[s.n.],1991.

[9]王佳文,李丽,易伟,等.3D NoC映射问题的动态蚁群算法[J].计算机辅助设计与图形学学报,2011,23(9):1614-1621.

WANG Jia-wen,LI Li,YI Wei,et al.A Dynamic Ant Colony Optimization Algorithm for 3D NoC Mapping[J].Journal of Computer-Aided Design &Computer Graphics,2011,23(9):1614-1621.

[10]何丽莉,王克淼,白洪涛,等.基于CMP的多种并行蚁群算法及比较[J].吉林大学学报:理学版,2010,48(5):787-792.

HE Li-li,WANG Ke-miao,BAI Hong-tao,et al.Multi Parallel Ant Colony Optimization Algorithms Based on CMP and their Comparison[J].Journal of Jilin University:Science Edition,2010,48(5):787-792.

[11]倪世宏,秦军立,苏晨.一种求解连续空间优化问题的动态蚁群算法[J].电光与控制,2009,16(12):12-15.

NI Shi-hong,QIN Jun-li,SU Chen.Dynamic Ant Colony Algorithm Used in Continuous Space Optimization[J].Electronics Optics &Control,2009,16(12):12-15.

[12]叶文,廉华耕,漆云海,等.无人机航路规划算法研究[J].电光与控制,2011,18(2):8-17.

YE Wen,LIAN Hua-geng,QI Yun-hai,et al.Path Planning Algorithm for UAV[J].Electronics Optics &Control,2011,18(2):8-17.

[13]DORIGO M.Optimization,Learning,and Natural Algorithms[D].Milan,Italy:Dipartimento di Elettronica,Politecnico di Milano,1992.

[14]DORIGO M,DI CARO G,GAMBARDELLA L M.Ant Algorithms for Distributed Discrete Optimization[J].Artificial Life,1999(5):137-172.

[15]BULLNHEIMER B,HARTL R F,STRAUSS C.A New Rank Based Version of the Ant System-Acomputational Study[J].Central Europen J Oper Rea Econom,1999(7):25-38.