下肢康复器械SVM建模的关键技术
刘 通,李海富,王丽荣,臧睦君
(1.长春理工大学 电子信息工程学院,长春 130022; 2.长春大学 电子工程学院,长春 130022;3.吉林大学 通信工程学院,长春 130012)
0 引 言
随着控制系统硬件的发展,系统模型的精度和复杂性都在逐步提高。而对于康复器械,传统的系统辨识往往需要使用单位阶跃等固定输入信号获取所需样本。由于康复器械的特殊性,在很多情况下,这类信号的响应无法采样得到,因此传统的建模方法无法满足该类系统的工程需要。目前,一些非结构化的机器学习模型也逐渐被应用于该领域的系统建模,其多数基于机器回归的理论模型[1,2],其中支持向量机是较好的方法之一。
支持向量机(SVM:Support Vector Machine)是由AT&T贝尔实验室的Vapnik及其研究小组于1995年在统计学习理论(SLT:Statistical Learning Theory)的基础上提出的一类新型的机器学习方法[3,4]。该方法相对人工神经网络而言,使用统计风险最小准则,有效地解决了人工神经网络泛化能力较差的问题,在很多领域中作为解决回归问题的重要工具。但支持向量机回归模型的效果依赖于训练参数的选取,而由于本课题模型的一些特殊性,导致在通常情况下,不能完全使用以非线性函数回归为蓝本的支持向量机的参数选取方法。因此,研究目前流行的参数选取算法在这类模型下的性质具有一定的工程实用价值,笔者通过仿真对比实验的方法得出一些主流算法的性能,讨论了这些算法在建模中的应用范围,并提出不同应用环境下算法的选取依据。
1 模型的特性分析与支持向量机建模
系统建模的基本问题,是对某系统y=f(x),x∈R1,y∈R2,求得映射g:R1→R2,使函数f和g之间的距离最小
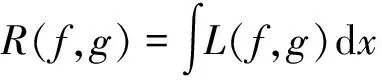
(1)
其中L定义为惩罚函数(Loss function),该式直接反映回归的精确度,被认为是回归器的反馈。系统模型中f为待求量,可通过采样得到样本对(x1,y1),(x2,y2),…,(xr,yr),xi∈R1,yi∈R2,通过回归方式求得g。控制系统的回归模型在本质上与非线性函数回归没有区别,通常情况下,驱动系统的离散模型在i+1时刻的输出可描述为
yi+1=f(yi,…,yi-n+1,ri+1,ri,…,ri-n+1)=f(xi)
(2)
其中xi=yi,…,yi-n+1,ri+1,ri,…,ri-n+1,n为系统的阶数。此外,样本集具有如下的前后递推关系[5]
[(yn-1,…,y0,rn-1,…,r0),yn]=(xn,yn)
[(yn,…,y1,rn,…,r1),yn+1]=(xn+1,yn+1)
(3)
这种特性说明,n阶系统当前时刻的输入与前n个状态有关,因此,相对非线性函数回归,训练样本不具有完全的独立性。对于固定结构的支持向量机,其最优参数的选择依赖于样本,因此,样本的特殊性也会导致最优参数的选择方法需要单独展开研究。
依据瓦普尼克的支持向量机基础理论,使用高斯径向基函数K(x,xi)=exp(-γ*‖x-xi‖2)为支持向量机的核函数,惩罚函数采用线性ε不敏感损失函数
Lε(x,y,f)=|y-f(x)|ε=max(0,|y-f(x)|-ε)
(5)
其中f是域X上的实值函数,x∈X,y∈R。核函数提供了由样本空间到可线性回归空间的映射,而不敏感损失函数则是式(1)的具体表达式
二次规划问题
(6)
在给定的参数下解决此二次规划问题就是支持向量机的学习过程。
2 支持向量机的参数选取方法
SVM的参数选取至今没有一个准确的方法,但其训练效果严重依赖于其参数的选取,所以从其创始之初参数选取的讨论就已经开始。对于经典支持向量机模型,定义不敏感损失函数的敏感度因子为C,核函数宽度参数的倒数为G。在本文中,C为式(5)中的ε,G为式(4)中1/γ。文献[6]首次提出了参数C的经验选取方法; 文献[7]进一步提出了基于响应和样本方差的经验公式; 文献[8]从噪声与损失函数的关联角度提出了损失参数的经验公式。这些早期的方法在一定程度上近似地解决了这一问题。
由于下肢康复训练器驱动系统的特殊性,对参数选择方法也有一些特殊要求:1)样本的前后递推关系使其并不完全独立,所以使参数特性与非线性函数回归不同,参数选取算法需要适应该模型; 2)在设备的设计、研发和中试阶段都需要不断调整系统参数甚至系统结构,因此,算法不需要过多人为干预就能得出有效结论; 3)能快速而较准确地找到最优参数。
随着计算机科学技术的发展,一些工程上常用的参数选取方法逐渐开始被广泛应用。这类工程算法通常以MSE(Mean Square Error,EMSE)和互相关系数(R2)作为目标函数的寻优算法,如粒子群算法(PSO:Particle Swarm Optimization)、网格搜索(GS:Grid-Search)和遗传算法(GA:Genetic Algorithm)。
由于粒子群算法相对遗传算法而言,种群之间的联系具有更明确的物理意义,因此,可把支持向量机中常用的交叉验证思想方便地引入粒子群,这类组合算法在近些年来的工程中也逐渐出现。
近几年来,提出一些针对通用支持向量机回归的算法,如文献[9]提出了一种启发式算法,该算法在精度和效率上都较工程寻优算法有巨大的优势。需要指出的是虽然文献[9]中没有在理论上明确指出依据,但认为启发式算法的成功得益于其采用经验概率模型的吉布斯采样参数估计。除了这些专用算法,一些改进型的工程寻优算法[10]也被广泛引用于这一领域。
目标函数寻优的参数选取方法的特点更适应于笔者需求,因此,笔者对3类常见的目标函数寻优算法通过仿真对比的方式,研究其优缺点及其适用范围,以此得到下肢康复器械使用SVM建模时,针对不同设备要求和实验环境采用的参数选择算法。
3 目标函数寻优算法及其仿真
常用的目标函数寻优算法中有代表性的是:以GS为代表的枚举迭代法、以GA为代表的全局优化算法以及以PSO为代表的局部与全局响应结合的方法。
样本的采集使用Matlab的Simulink工具箱,搭建样本采集系统(见图1),以采集到的样本前6 s作为训练集,后40 s为测试集,采样间隔0.1 s,因此,得到60个训练样本和400个测试样本,对样本进行(-1,+1)的归一化后分别作为训练集和测试集。
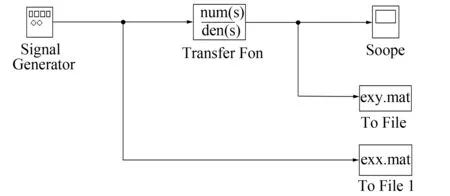
图1 Simulink采样仿真系统
笔者使用台湾国立大学林智仁教授开发的Libsvm系列工具箱为支持向量机回归仿真工具,使用其Matlab版本作为平台进行研究。该工具箱提供了完善的核函数、参数和训练效果等接口,笔者以训练参数接口作为目标函数的自变量,训练效果反馈接口作为目标函数的因变量。自变量具体为惩罚参数C和高斯径向基核宽度G,而因变量为训练集和测试集上的EMSE和R2。以此为基础,分别在SVM外层搭建3种目标函数寻优算法的参数寻优函数,用于分析其特点。
3.1 GS算法
GS算法的基本步骤:
1)对给定的参数范围和步长,枚举产生参数样本对;
2)对每个参数样本对执行SVM训练,并且在训练集上执行训练;
3)求得每个参数样本的MSE;
4)取MSE最小的参数样本作为最终的训练参数。
设置C、G的迭代范围均为(2-8,28),迭代步长均为2-0.5,迭代找到的最优参数C=8,G=0.015 625。该参数下,训练集EMSE=0.002 303 64,R2=0.995 528,测试集EMSE=0.004 079 75,R2=0.992 219。输出效果比对如图2所示。图2中纵坐标为系统输出归一化值,横坐标为样本序列号。其中实线连接的黑色空心圆为Simulink仿真系统输出,虚线连接的浅色空心三角为SVM预测输出,两者在波形上完全近似,仅在局部区域存在偏差,实际效果与所得的实验统计数据基本一致。
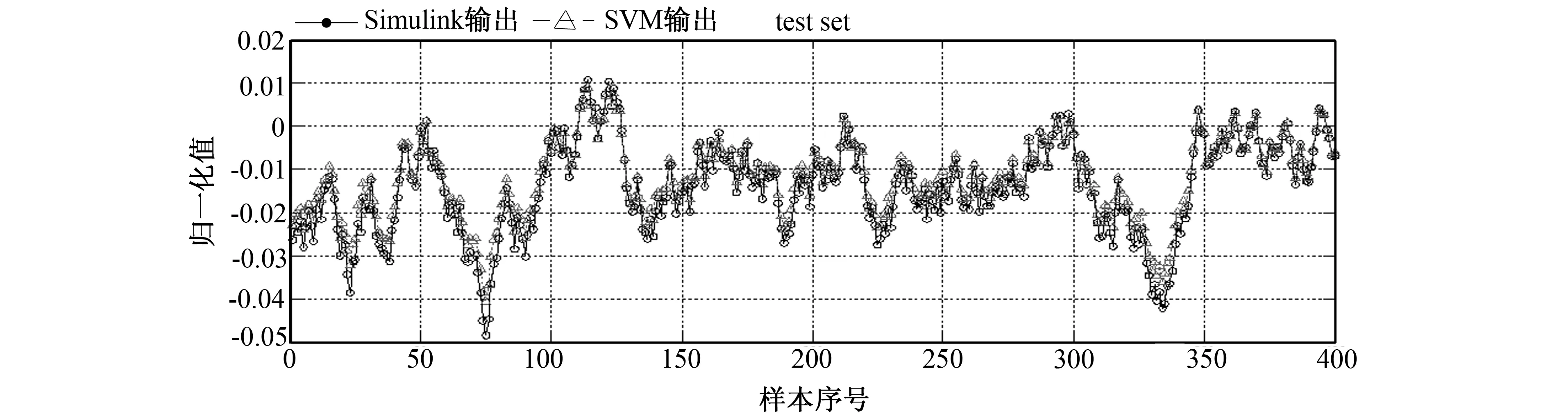
图2 GS算法的效果
由于GS是一种没有随机量的算法,而SVM本身也没有随机量,因此,该算法的实验结果绝对稳定(无论进行多少次实验均能得到相同的结果)。这种特性适用于容易造成二次损伤的下肢残障病人专用的器械。而从实验效果看,回归效果也非常优秀。但需要指出的是,由于这类算法过于依赖计算量,其运算量对参数的个数以及训练样本数量呈灾难性,因此,不适于大样本回归以及目前较热门的多核支持向量机[11,12]。
3.2 GA算法的基本步骤
1)初始化。设置进化代数计数器t=0,设置最大进化代数T,随机生成M个个体作为初始群体P(0)。
2)个体评价。计算群体P(t)中每个个体的适应度。
3)选择运算。将选择算子作用于群体。以优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作建立在群体中个体的适应度评估基础上。
4)交叉运算。将交叉算子作用于群体。交叉是指把两个父代个体的部分结构加以替换重组成新个体的操作。遗传算法中起核心作用的就是交叉算子。
5)变异运算。将变异算子作用于群体。即对群体中个体串的某些基因座上的基因值进行变动。 群体P(t)经过选择、交叉和变异运算后得到下一代群体P(t1)。
6)终止条件判断。若t=T,则以进化过程中所得到的具有最大适应度的个体作为最优解输出,终止计算。
使用与3.1节相同的样本和迭代范围,设置参数为最大进化代数100,种群数量20。由于GA算法不稳定,并且在理论上不保证每次都能找到最优解,因此,通过多次重复实验的方式检验其效果和稳定性。笔者列出其中15次实验结果(见表1),表1中,依次统计了对训练集本身进行预测输出以及对测试集进行输出的EMSE和R2,充分体现其精确度和泛化能力。从结果可以看出,GA算法在本课题中表现非常不稳定,有时会得到非常理想的结果,如第7组、第12组和第13组,但多数情况下结果并不理想,甚至完全不可用。
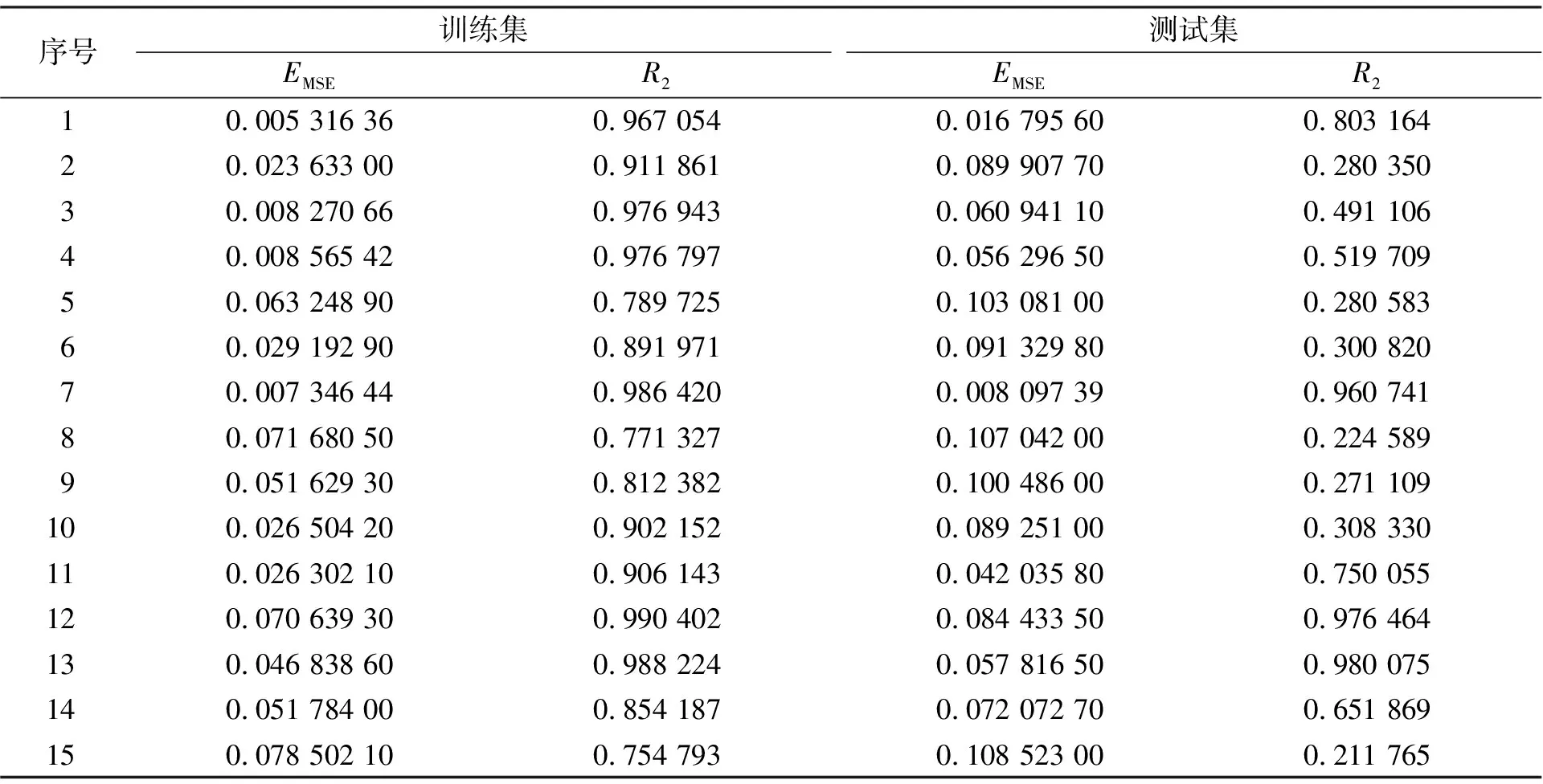
表1 GA的实验数据统计
虽然GA算法在分类问题以及通用回归问题中有良好的表现[13,14],但该算法无法满足要求,可能是两方面原因导致的:1)该课题中样本不完全独立会导致目标函数有更多的局部最优点,而GA算法在局部最优点过多的情况下并不十分有效; 2)GA算法在局部最优点之间存在的联系过于随机化,使迭代效率非常低。因此,在本课题中,GA算法仅适用于不关注参数稳定性的实验室讨论。
3.3 CV-PSO算法
CV-PSO(Cross Validation-Particle Swarm Optimization)算法的基本步骤如下:
1)种群随机初始化;
2)通过交叉验证规则生成不同样本集;
3)在不同样本集上对种群内的每个个体计算适应值(fitness value),其与最优解的距离有关;
4)种群根据适应值进行复制,并保留最佳适应值的解;
5)判断是否满足中止条件,若不满足,则跳转到2); 若满足,则以找到的最佳适应值的解为最终结果。
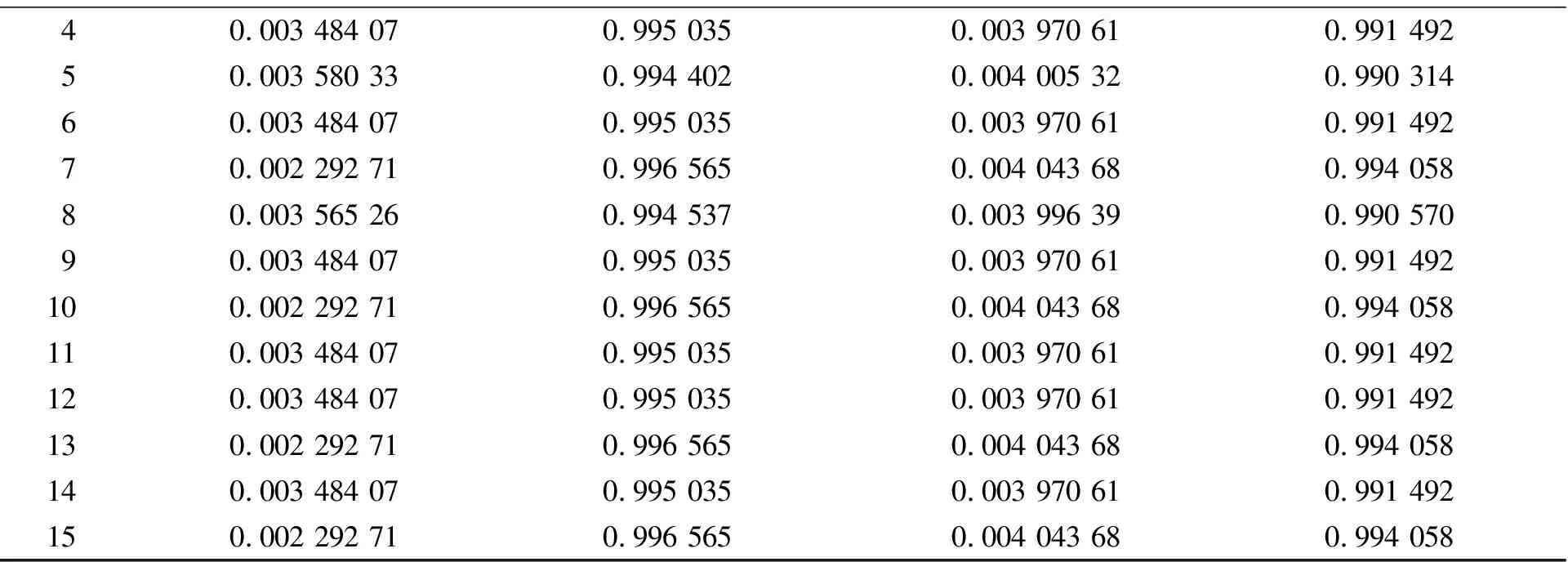
笔者选取与3.2节相同的最大运算代数和种群数量,并引入3折交叉验证。由于粒子群算法同样是不稳定的,因此,通过多次重复实验验证其性能与稳定性,表2为其中15次实验结果,实验结果的统计方式与表1相同。
可看出虽然结果不是绝对稳定,但第1、2、4、6、9、11、12、14组的结果收敛于相同的最优解,而且其他解也较为稳定地收敛在性能很好的位置。在该课题中,CV-PSO算法的效果得益于:1)比GA算法具有更明确的种群联系; 2)引入的交叉验证算法极大地提高了系统的泛化能力; 3)局部加种群联系的响应方法对控制系统中样本不独立问题的包容性更好。因此,相对于GS算法,CV-PSO适用于对稳定性没有绝对要求的情况,而对于实时性要求不高的系统,GS依然是一种最有效的选择。

表2 CV-PSO的实验结果统计
(续表2)
40.003 484 070.995 0350.003 970 610.991 49250.003 580 330.994 4020.004 005 320.990 31460.003 484 070.995 0350.003 970 610.991 49270.002 292 710.996 5650.004 043 680.994 05880.003 565 260.994 5370.003 996 390.990 57090.003 484 070.995 0350.003 970 610.991 492100.002 292 710.996 5650.004 043 680.994 058110.003 484 070.995 0350.003 970 610.991 492120.003 484 070.995 0350.003 970 610.991 492130.002 292 710.996 5650.004 043 680.994 058140.003 484 070.995 0350.003 970 610.991 492150.002 292 710.996 5650.004 043 680.994 058
4 结 语
笔者针对支持向量机用于下肢康复训练器驱动系统建模时的训练参数选取问题进行了研究,通过对比实验的方法讨论了当前比较流行的3种目标函数极值寻优算法。实验结果表明:GS算法绝对稳定而且效果很好,但运算开销大,仅适用于单核双参数的情况; GA算法适用于不考虑参数问题的支持向量机实验室讨论,而不适合于此类问题的工程应用; CV-PSO算法较为稳定,且性能很好,适合于除个别(要求性能绝对稳定)情况下的多数工程应用。对3种不同算法的实验讨论以及选取依据的提出解决了下肢康复训练器驱动系统建模的难点。
参考文献:
[1] 康皓,林和平.基于模糊回归的模糊决策模型的设计与实现[J].吉林大学学报:信息科学版,2005,23(2):107-112.
KANG Hao,LIN He-ping.Design and Realization of Fuzzy Decision Making Model Based on Fuzzy Regress[J].Journal of Jilin University:Information Science Edition,2005,23(2):107-112.
[2]林和平,张秉正,乔幸娟.回归分析人工神经网络[J].吉林大学学报:信息科学版,2010,28(2):147-152.
LIN He-ping,ZHANG Bing-zheng,QIAO Xing-juan.Regression Analysis Artificial Neural Network[J].Journal of Jilin University:Information Science Edition,2010,28(2):147-152.
[3]VAPNIK V.The Nature of Statistical Learning Theory[M].New York:Springer,1999.
[4]MOLA A.A Tutorial on Support Vector Regression[R].London,UK:Royal Holloway College,University of London,1998.
[5]梁华,李应红,尉询楷,等.航空发动机的支持向量机自适应PID控制[J].航空动力学报,2007,22(1):137-141.
LIANG Hua,LI Ying-hong,WEI Xun-kai,et al.Support Vector Machines PID Adaptive Control in Aeroengine[J].Journal of Aerospace Power,2007,22(1):137-141.
[6]MATTERA D,HAYKIN S.Support Vector Machines for Dynamic Reconstruction of a Chaotic System[C]∥Advances in Kernel Methods-Support Vector Learning.Cambridge,MA:MIT Press,1999.
[7]CHERKASSKY V,MA Y.Selection of Meta-Parameters for Support Vector Regression[C]∥Proceedings of the International Conference on Artificial Neural Networks.Madrid,Spain:Springer,2002:687-693.
[8]SMOLA A J,MURATA N,SCHOLKOPF B,et al.Asymptotically Optimal Choice of Epsilon-Loss for Support Vector Machines[C]∥Proceeding of the International Conference on Artificial Neural Network.Berlin,Germany:Springer,1998:105-110.
[9]刘靖旭,蔡怀平,谭跃进.支持向量回归参数调整的一种启发式算法[J].系统仿真学报,2007,19(7):1540-1543.
LIU Jing-xu,CAI Huai-ping,TAN Yue-jin.Heuristic Algorithm for Tuning Hyperparameters in Support Vector Regression[J].Journal of System Simulation,2007,19(7):1540-1543.
[10]ZHOU Tao,ZHANG Yan-ning,YUAN He-jin,et al.SVM Based on Improvement Particle Swarm Optimization Algorithm[J].Computer Engineering and Applications,2007,43(15):44-46.
[11]杨海燕,周永权.一种支持向量机的混合核函数[J].计算机应用,2009,29(12):173-178.
YANG Hai-yan,ZHOU Yong-quan.Mixture Kernel Function of Support Vector Machines[J].Journal of Computer Applications,2009,29(12):173-178.
[12]颜根廷,马广富,肖余之.一种混合核函数支持向量机算法[J].哈尔滨工业大学学报,2007,39(11):1704-1706.
YAN Gen-ting,MA Guang-fu,XIAO Yu-zhi.Support Vector Machines Based on Hybrid Kernel Function[J].Journal of Harbin Institute of Technology,2007,39(11):1704-1706.
[13]王建中,刘凌,徐金阳.基于遗传算法与支持向量机的日流量预测[J].水电能源科学,2008,26(4):14-17.
WANG Jian-zhong,LIU Ling,XU Jin-yang.Daily Flow Forecasting Based on Genetic Algorithm and Support Vector Machine[J].Water Resources and Power,2008,26(4):14-17.
[14]陈果.基于遗传算法的支持向量机分类器模型参数优化[J].机械科学与技术,2007,26(3):347-350.
CHEN Guo.Optimizing the Parameters of Support Vector Machine’s Classifier Model Based on Genetic Algorithm[J].Mechanical Science and Technology,2007,26(3):347-350.

