基于贝叶斯理论的刀具维修决策模型

刘 念，李建兰，陈 刚，丁宏刚，康 乐，严 野

（1. 华中科技大学 能源与动力工程学院，武汉 430074；2. 中国人民解放军91760部队，江门 529145）

0 引言

随着生产技术的高速发展，电力和机械等行业的设备日趋大型化和精密化，设备的正确维修对企业的安全和经济生产都具有重要意义。设备工作性能的好坏、效率的高低都与维修有关，对故障原因症候诊断的正确处理以及维修方式的运用，这些都需要维修计划的指导[1]。维修策略的选择与时机的确定成为研究者们关注的热点问题。

近年来，国内外许多学者对维修决策进行了研究，提出了各种决策模型。Murray A和Ko T J等人利用神经网络或自回归时序等模型对磨损量进行计算或监测[2～4]，CAO X和陈保家等人利用比例危险模型或Logistic回归模型预测刀具有效剩余寿命[5,6]。周奇才等人提出了基于风险的维修决策，对堆垛机的风险进行定量分析并利用风险为决策目标建立维修策略以降低堆垛机的运行风险[7]。程志君等人针对部件间存在经济相关性的复杂系统，提出一类基于机会策略的视情维修优化模型，解决系统层事后维修与视情维修的综合优化问题[8]。王进才等人运用马尔可夫决策模型，提出了以费用效果为指标的维修策略[9]。罗运虎等提出基于风险的用户可靠性需求决策模型，得到了用户可靠性需求的最优值[10]。此外，林月平等人将最短路径算法应用在工程装备应急维修决策中，提高了维修保障效率[11]。刘晓平等人将进化蒙特卡洛方法引入机械故障诊断的特征选择，提高机械故障诊断精度和诊断效率[12,13]。还有一些学者开发了关于维修决策的软件支持系统，李敏等人引入了基于状态的维修，设计并开发了自行火炮状态维修决策支持系统(CBMDSS)[14]；吴军等人提出基于隐马尔科夫链模型的数控装备可靠性预测方法，在此基础上, 开发了数控装备可靠性预测原型软件系统，该系统对于提高数控装备利用率、减少数控装备维修费用以及延长数控装备使用寿命等具有重要的意义[15]。

在维修实际中，由于设备自身特性以及实际运行条件等各种原因，设备状态劣化的发展过程通常不是严格按照统计出来的性能曲线的过程发展，而是劣化程度存在偏差的情况[16～18]。针对这一问题，本文根据修正的思想将先验概率加以修正，建立基于贝叶斯理论的维修决策模型，以实现基于设备实际状态的维修决策。

1 基于贝叶斯理论的维修决策模型

基于贝叶斯理论的维修决策模型，从刀具个体差异性角度出发，根据贝叶斯理论得到刀具当前状态的后验分布，然后再结合性能曲线确定刀具未来某一时刻状态，得到不同时刻点的维修成本，最后根据基于维修成本最小化的原则确定最优的维修方案。

1）状态向量A

状态向量指设备的全部可能状态的集合。一般，设备状态可分为正常、不正常和故障三种状态。由于设备处于故障状态时必须进行维修，而本文讨论的主题是选择最佳设备维修时机，因此，故障状态不需要考虑，设备状态只需考虑正常和不正常即可。设设备状态向量A为：

根据产品质量，产品状态分为合格和不合格，因此，定义产品状态向量C为：

2）先验概率和后验概率

先验概率指根据以往经验和分析得到的概率。设备性能曲线通常由历史统计数据分析得到，如图1所示，反映了设备正常/异常概率与工作时间的关系。因此，设备状态的先验概率可以由性能曲线获得，根据设备运行时间t即可在性能曲线上得到设备正常的先验概率Pt1(A1)以及设备不正常的先验概率Pt1(A2)。

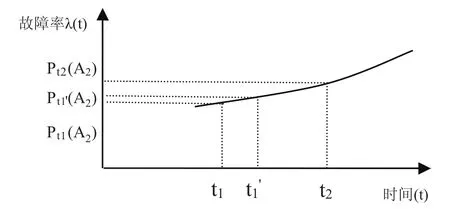
图1 设备性能曲线

后验概率指利用新的信息修正先验概率后获得的更接近实际情况的概率估计，表示为Pt1(A2|B)，其中，B为抽样事件：在t1时刻，在设备加工后的产品中抽取m件产品，有n件不合格，其余合格。本文将利用贝叶斯理论来计算后验概率。

根据贝叶斯理论，设有构成事件完备组的2个事件Ai（i=1，2），t1时刻各事件发生的概率分别为Pt1(Ai)，独立事件B发生的概率为P(B)。假设事件B在事件Ai条件下发生的概率为Pt1(B|Ai)，则t1时刻事件Ai在事件B条件下发生的概率为：

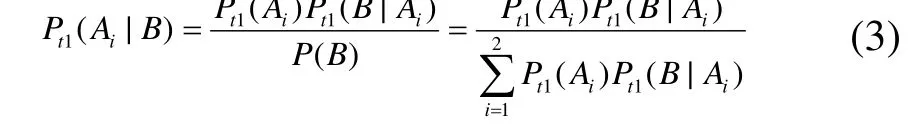
公式（3）中， Pt1(Ai|B)为t1时刻事件Ai的后验概率， Pt1(Ai)为t1时刻事件Ai的先验概率， B为观测样本事件。

根据条件概率公式可以得到：

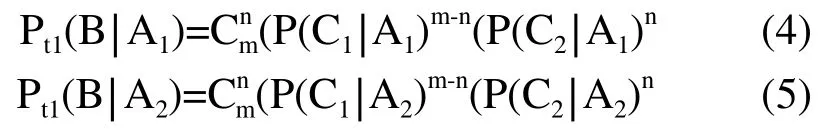
式（4）、（5）中m, n分别为抽样总数和抽样次品数，将式（4）、（5）代入公式（3）中，得到t1时刻设备状态为正常、异常的后验概率Pt1(Ai|B)（i=1,2）为：

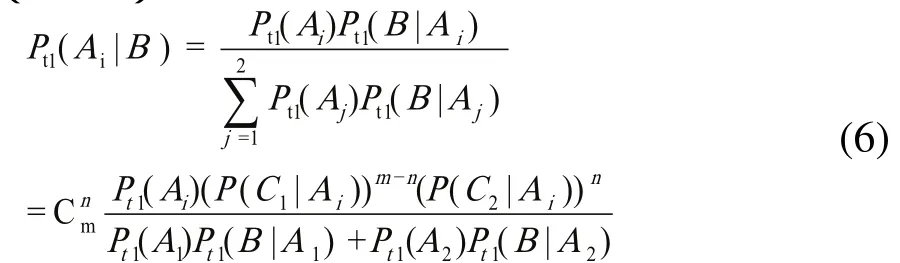
后验概率Pt1(Ai|B)是在设备统计概率Pt1(Ai)基础上修正得到，通过对设备设置抽样事件增加信息量，克服了统计概率不针对个体的缺点，得到更加符合设备自身实际的概率分布。后验概率的引入，为更准确地评价设备所处状态提供了一个途径，也为正确选择维修决策提供了基础，是一种简单的基于状态的维修策略。

根据后验概率Pt1(A2|B)在性能曲线中得到相应的运行时间t1’，即性能曲线上t1’时刻概率Pt1’(A2)=Pt1(A2|B)，记Pt1’(A2)为考虑设备实际运行状态后t1时刻对应的当量概率，则有Pt1’(A2)=Pt1’(A2)=Pt1(A2|B)，反映了设备的实际劣化状态。修正后的概率才是设备实际的故障概率。应当是根据修正后的概率，找到一个对应的时间点（当量时间），就相当于设备已经运行了更长的时间，所以才有更高的故障率。从时间上说，由于设备加剧了劣化，所以更接近于失效，寿命变短，不能运行到预期的时间点。当然，如果设备保养得好，也有可能是修正后的概率更低，那就意味着设备可以使用更长的时间。

设下一维修时刻为t2时刻，由当前修正后的点t1’时刻容易得到下一维修时刻t2时刻，并在性能曲线中得到t2时刻对应的设备状态异常的概率Pt2(A2)，如图1所示。继而得到t2时刻设备状态正常概率Pt2(A1)=1- Pt2(A2)。

3）概率矩阵P

把某一时刻设备各状态的概率组成一个矩阵，称为该时刻的概率矩阵P。设t1时刻的概率矩阵为P1，t2时刻的概率矩阵为P2，则有：

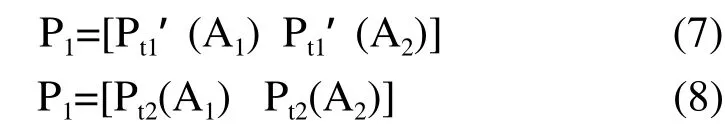
4）维修决策向量Q

维修决策向量指设备全部可能维修方案的集合，设维修方案包括立即维修和暂不维修。则维修决策向量Q为：

5）约束条件

当设备运行时间超过最大允许运行时间或抽样事件次品率超过允许值时，均需立即维修。为了保证设备安全性，设约束条件：

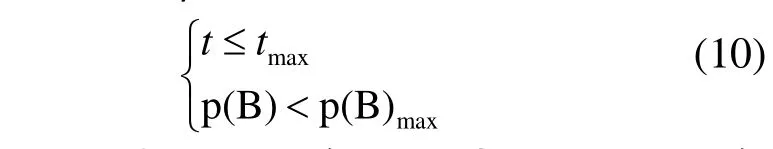
公式（10）中，t为设备运行时间，tmax为设备最大允许运行时间， p(B)为抽样次品率，p(B)max为抽样允许最大次品率。

6）维修成本矩阵F

维修过程中可能存在零件更换、生产产品质量、设备停机和人力资源等方面的损耗，同时零件的使用寿命也影响着维修的总成本，当零件使用时间超过其设定寿命时，超出的使用时间会减少厂家对零件的投资成本，本文把因为零件使用寿命延长所减少的投资称为节省投资成本；当零件超出其寿命时，节省投资成本为正值，反之为负值。因此，本文所讨论的维修过程中的成本包括次品成本、零件成本、停机成本、人工成本和节省投资成本。在给定设备状态下，不同的决策行为会有不同的维修成本。将不同设备状态、决策行为下，各维修成本的数值表示成一个矩阵，称为维修成本矩阵，记为F。因此，采取qi（i=1,2）维修决策时的维修成本矩阵Fi为：

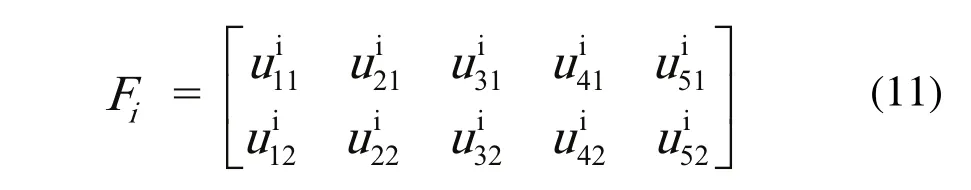
公式（11）中各元素分别表示采用决策qi时的各维修要素。分别是设备状态为正常（A1）、不正常（A2）时的次品成本；分别是设备状态为正常（A1）、不正常（A2）时的零件成本；分别是设备状态为正常（A1）、不正常（A2）时的停机成本；分别是设备状态为正常（A1）、不正常（A2）时的人工成本；分别是设备状态为正常（A1）、不正常（A2）时的节省投资成本。

7）维修总成本U

维修总成本是各维修决策方案所产生的维修成本。维修总成本矩阵可表示为：

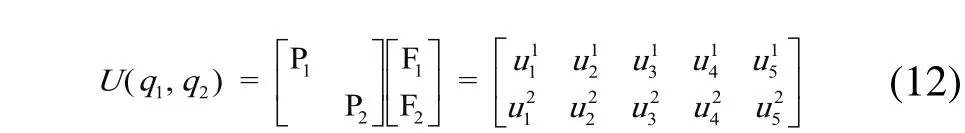
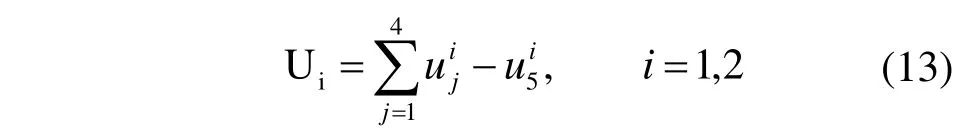
根据最小维修成本的原则，得到基于贝叶斯理论维修决策模型的最优决策qmax为：

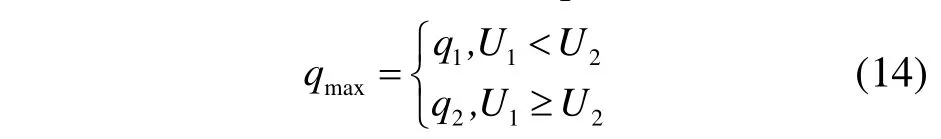
若U1＜ U2,选取q1为维修决策；反之选取q2为维修决策。

2 加工中心刀具维修时机决策

刀具是加工中心的重要部件，刀具状态的好坏直接影响着工件的加工质量。因此，刀具的合理更换是生产质量和经济性的重要保证。已知厂家提供的刀具性能曲线如图2所示，刀具平均寿命为加工工件950件，刀具已经加工工件数为800件，在刀具加工的产品中，抽取300件产品，有1件不合格，其余合格。

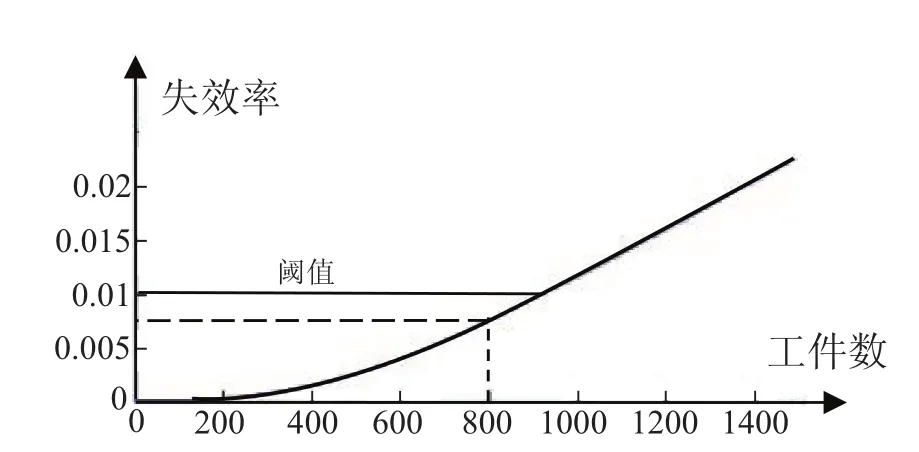
图2 刀具性能曲线

工厂历史运行数据表明，刀具状态正常时产品合格率为99.9%，刀具状态不正常时产品合格率为99%。厂家规定：产品抽样不合格率不得高于1%，刀具加工工件数不得超过1200件。以一天为时间段，刀具状态为正常、不正常时产生的次品数分别为1件和5件，一件次品损失500元，停机时间一小时损失30000元，因为刀具原因而停机后维修时间一般为0.5小时，即每次停机损失为15000元，刀具寿命延长一天节省的投资成本为1000元。刀具维修过程中，维修类型分为预防性维修和故障维修。当设备状态正常时，实施预防性维修；当设备状态不正常时，实施故障维修。当前时刻（t1时刻）和下一时刻（t2时刻）的维修成本如表1、表2所示。

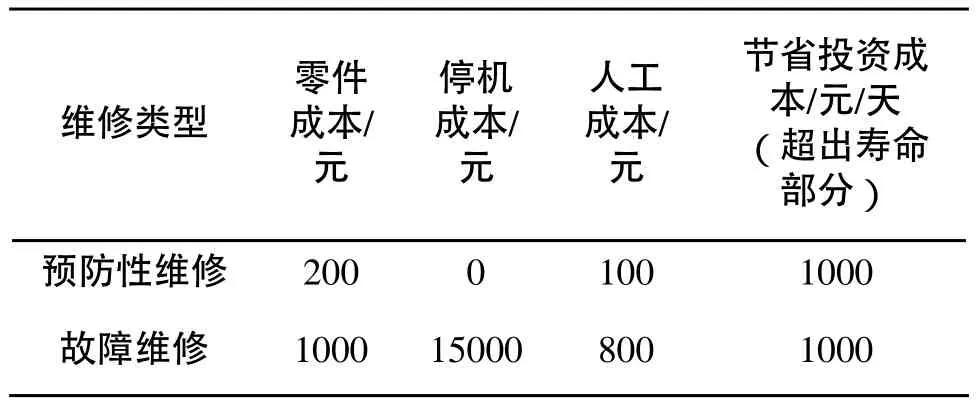
表1 t1时刻维修成本表

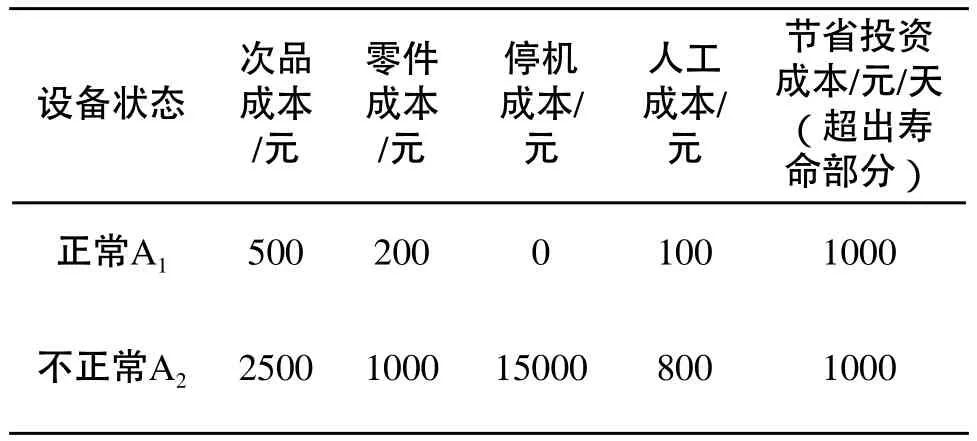
表2 t2时刻维修成本表

在图2中，横坐标为刀具已加工工件数，纵坐标为刀具失效率。由刀具加工工件数为800，可知其先验失效率为0.007，即刀具先验概率分布为：

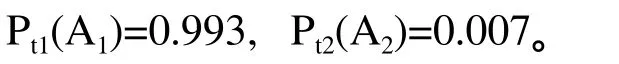
由已知条件可知，当设备状态为正常或不正常时，产品合格率分别为：

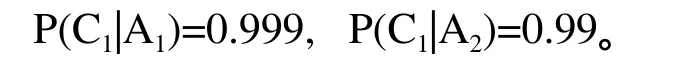
将上述先验概率与条件概率的数据带入公式（6）和公式（7），得到此时刀具状态的后验概率为：

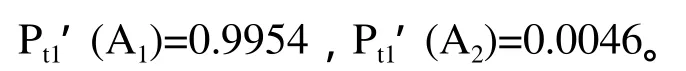
通过图2和Pt1’(A2)，得到修正后的当量工件数为680件，按每天加工100件工件，往后推一天得到第二天t2时刻加工工件数为780，由图2可知t2时刻刀具状态分布为：

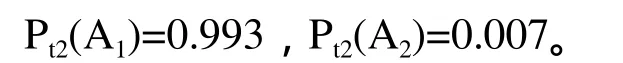
得到t1时刻和t2时刻概率矩阵分别为：

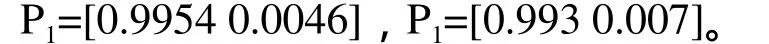
因t1时刻和t2时刻刀具均未超出平均寿命，其节省投资成本分别为：

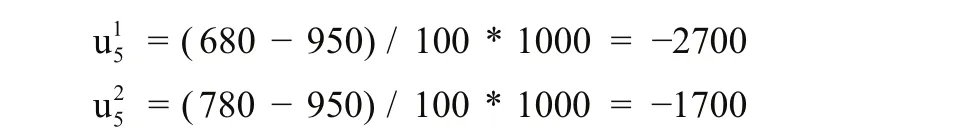
采用决策q1即立即维修时，维修类型为预防性维修，记此时维修成本矩阵为F1；采用决策q2即暂不维修时，维修类型为预防性维修或故障维修，记此时维修成本矩阵为F2，有：

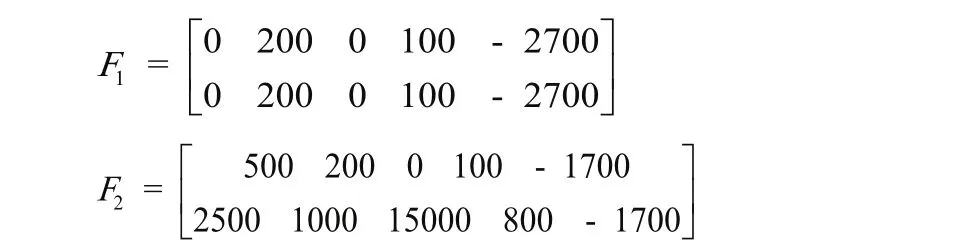
得到：

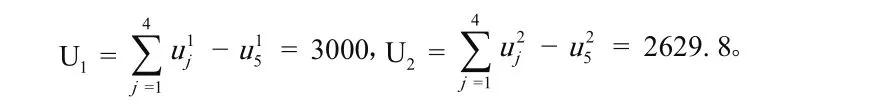
因为U1＞ U2，所以最优决策为q2：暂不维修。

曲线中t2时刻异常概率Pt2(A2)可以作为t2时刻的先验概率，在t2时刻时，同样可以采用抽样事件增加信息量，得到t2时刻的后验概率，不断修正刀具所处状态，使其更真实地反映劣化状态，并在此基础上得到t2时刻的最优维修决策，如此反复，依次得到下一时刻点的最优维修决策。

3 结束语

本文建立了一种基于贝叶斯理论的维修决策模型，适用于设备先验概率已知、抽样事件容易实施的维修决策的选择。刀具的维修决策结果表明，基于贝叶斯理论的后验概率不仅能较好地修正先验概率，更为重要的是反映了设备更为真实的劣化状态，为维修决策提供了重要依据，从而减少设备的维修不足和过度维修，保证了设备的安全运行和经济运行。本文研究成果为企业施行状态检修提供了一种途径，具有有益的参考意义。

[1] 黄树红,李建兰.发电设备状态检修与诊断方法[M].北京:中国电力出版社,2008.

[2] Hatzipantelis E, Murray A, Penman J. Comparing hidden Markov models w ith arti fi cial neural network architectures for Condition M onitoring App lications[C]//Fourth International Conference on Artificial Neural Network.UK: Cambridge,1995:369-374.版社,2010.

[2] 张根保.现代质量工程[M].北京:机械工业出版社.2007.7.

[3] 金春玲.生产过程中的统计过程控制[J].电子质量,2007(9):51-54.

[4] 张公绪,等.常规控制图标准及其应用[M].北京:中国标准出版社.2000.

[5] Donald J,Wheeler and David S.Chambers.Understanding Statistical Process Control[J].Second Edition.SPC Press In c.2000.(2):45-50.

[6] 张公绪,孙静.统计过程控制与诊断第二讲[J].质量与可靠性,2002(2):45-49.

[7] 张公绪,孙静.统计过程控制与诊断第九讲[J].质量与可靠性,2003(3):42-46.

[8] 黄玲,等.电子元器件制造过程中非正态工艺参数的统计过程控制技术[J].电子质量,2010(1):38-40.

[9] 梁国明.制造业过程质量控制与检验常用统计方法读本[M].北京:中国标准出版社,2006.

[10] 马健诚,等.面向质量的制造过程控制管理研究[J].机床与液压.2008(2):17-19.