基于观测器的半主动悬架天棚控制设计与实现
李彤,姚嘉凌,王明海,李林姗,钟景辉
(南京林业大学汽车与交通工程学院,南京 210037)
0 引言
车辆悬架系统性能的优劣直接影响车辆的乘坐舒适性和操纵安全性。传统的被动悬架由于其参数固定从根本上造成了两者的矛盾,主动悬架虽有较大的响应范围,能取得好的减振效果,但成本高、结构复杂及能耗大而难以推广使用。半主动悬架其减振器的阻尼系数在一定范围内可以调节或者其承载弹簧的刚度是可以改变的,半主动悬架的性能可达到或接近主动悬架的性能[1]。
天棚阻尼控制是半主动悬架的经典算法[2],使用可靠,其需要采集车身的绝对速度及车身与轮胎之间的相对速度,但从目前的技术水平来看,通过直接测量来获得某些状态观测量(如车身的绝对速度)是相当困难的。克服这种困难的途径之一是重构系统的状态,并用这个重构的状态来代替系统的真实状态来实现所需的状态反馈[3-4]。
运用Kalman滤波器进行状态估计,减少实际测量的成本逐渐引起了学者们的广泛关注[5]。虽然Kalman滤波器对速度的估计比较准确,但是在实际使用中,由于受到系统非线性,参数变化,以及干扰等因素,状态观测器不一定能保证全局渐近稳定性、收敛性。因此,在Kalman滤波器的设计的基础上,设计了滑模观测器,克服了一般状态观测器的缺点,保证了系统全局渐进稳定性,并对两个观测器的效果进行了对比。
1 汽车半主动悬架系统的模型研究
相对于被动悬架,半主动悬架增加了减振器可控力fd,两自由度模型如图1所示。运动微分方程为:
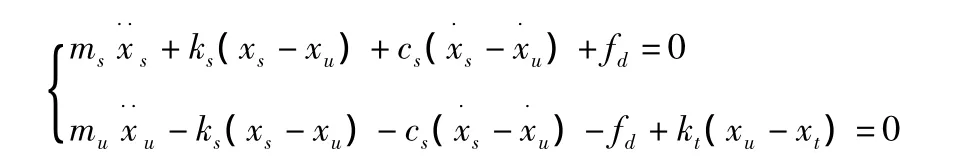
式中:ms—簧载质量;
mu—非簧载质量;
ks—悬架弹簧刚度;
kt—轮胎的刚度;
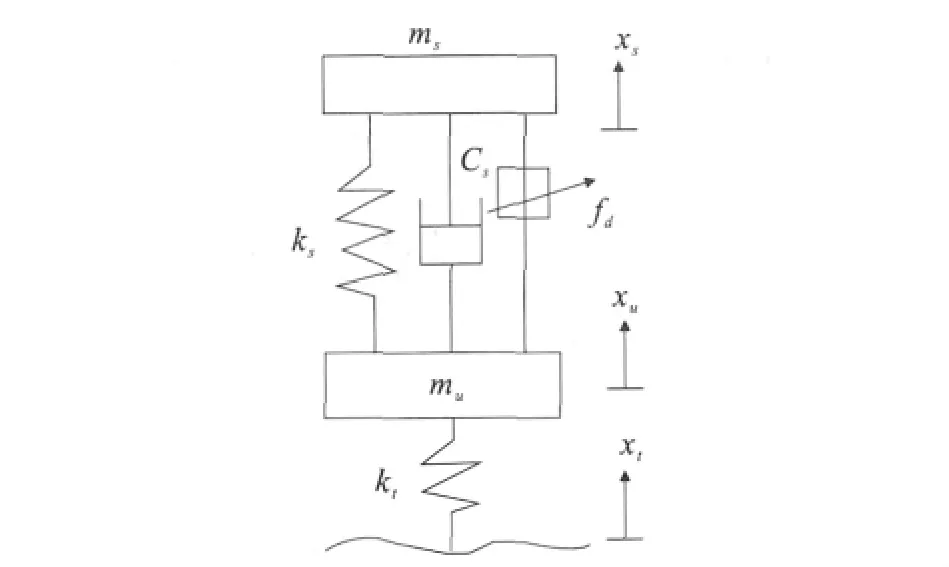
图1 半主动悬架1/4模型
cs—悬架机械阻尼;
fd—可控制阻尼力;
xt—地面随机激励位移;
xs—簧载质量位移;
xu非簧载质量位移。选取状态变量:

系统的空间状态方程:
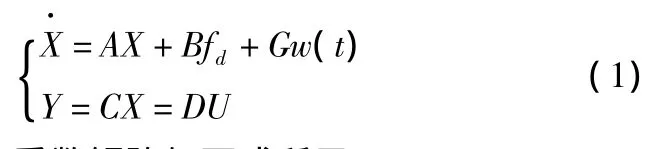
其中,方程中的各系数矩阵如下式所示:
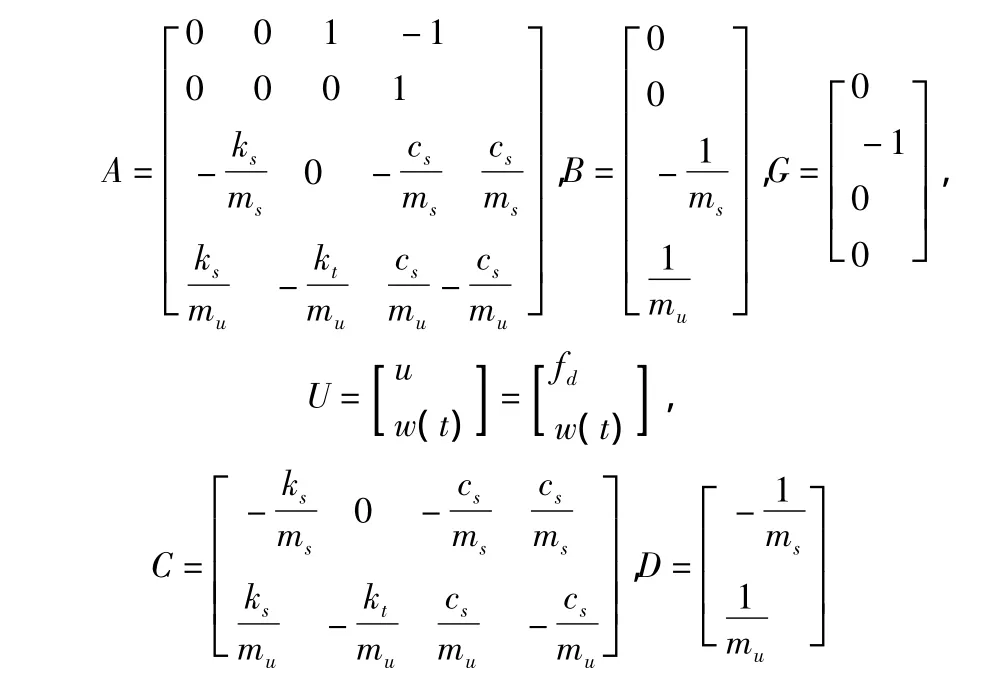
u为减振器的控制力,即fd。
2 状态观测器的设计与仿真
2.1 Kalman滤波器的设计
系统的Kalman滤波器就是最优观测器。利用Kalman滤波器对系统进行最优控制是非常有效的。车辆在道路上行驶,路面的扰动可以看作是滤波白噪声,则可以将路面扰动看作为系统模型噪声,而用传感器测量加速度信号,或多或少的会有一些干扰,这些干扰可以看作是量测噪声。采用Kalman滤波算法求解观测器的增益 ,从而通过观测器进行状态估计(观测器原理如图2所示),比采用极点配置方法进行状态估计更为合适。

图2 状态观测器原理图

这里假定w(t),v(t)分别为零均值的一维随机噪声干扰输入和2维随机白噪声过程。w(t)与v(t)两噪声过程均平稳且互不相关。
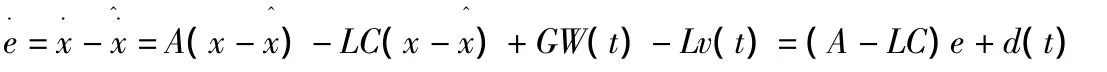
其中:d(t)=Gw(t)-Lv(t)
通过计算可知系统是完全可观测的。所以系统的最优估计器为:

式中L=PoCTRo
其中Po为以下Riccati方程的解:
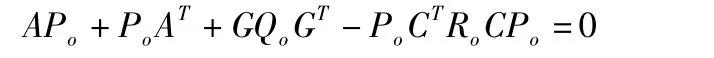
可以证明,Riccati方程的解Po就是估计误差的协方差,而此协方差的迹(trPo)即为误差方差。
2.2 滑模观测器的设计
在实际使用中,由于受到系统非线性,参数变化,以及干扰等因素,状态观测器不能保证全局渐近稳定、收敛性和鲁棒性。因此本文在Kalman滤波器的基础上加入滑模sgn开关量Ko(y- ),设计滑模观测器,保持系统全局渐近稳定性[6]。滑模观测器状态方程:
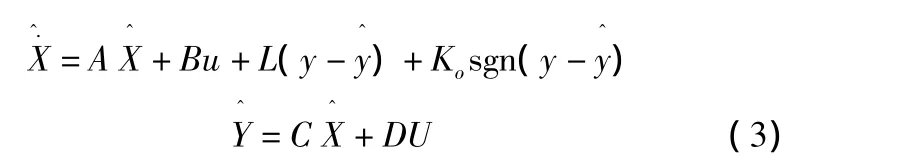
本文用圆判断的方法[7-9],选取Ko= ρG,ρ≥0.此外为了避免抖振,用饱和函数代替开关函数:xp=Ko.sat
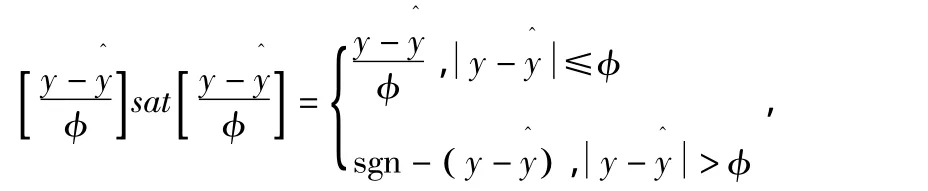
φ为误差界限宽度。当观测器的误差超出这个边界宽度时,滑模开关量将变得不连续。
3 基于观测器的天棚控制仿真验证
3.1 天棚阻尼控制算法

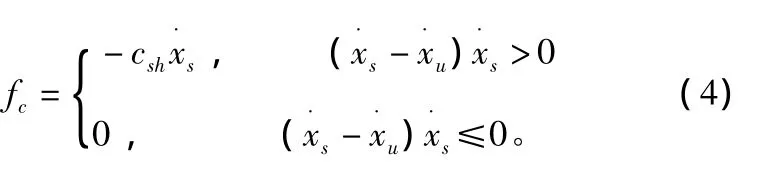
3.2 基于观测器的天棚控制仿真验证
以Matlab/Simulink作为仿真语言平台,对基于Kalman滤波观测器的天棚控制进行仿真计算,(图3)被动悬架为比较对象,道路为B级路面,车速为60 km/h,采样时间为t=0.01 s,ms=160 kg,mu=20 kg,ks=10 000 N/m,kt=100 000 N/m,cs=200 N·s/m,csh=2 500 N·s/m,cp=1 000 N·s/m(被动悬架)。
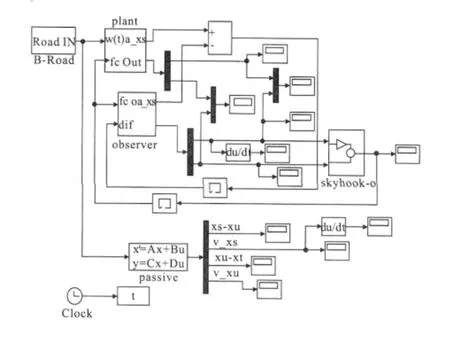
图3 基于观测器的半主动悬架仿真模型
滑模观测器和Kalman滤波器的悬架绝对速度和相对速度估计值以及真实值3者之间比较结果如图4所示。
由图4可以看出:滑模观测器对绝对速度和相对速度的观测效果比Kalman滤波器的观测效果要好,估计值比较接近理想值。

图4 基于滑模观测器和Kalman滤波器的悬架绝对速度、相对速度估计值对比图
基于滑模观测器、Kalman滤波器的天棚控制以及被动悬架悬架的加速度、悬架动挠度以及轮胎动载荷对比如图5所示。
由图5可以看出,基于滑模观测器的天棚控制和基于Kalman滤波器的天棚控制衰减了车身振动的加速度,降低了悬架的相对位移,但是轮胎的动载荷却比被动悬架稍有增大,基于滑模观测的天棚控制的控制效果略好与基于Kalman滤波器的天棚控制。

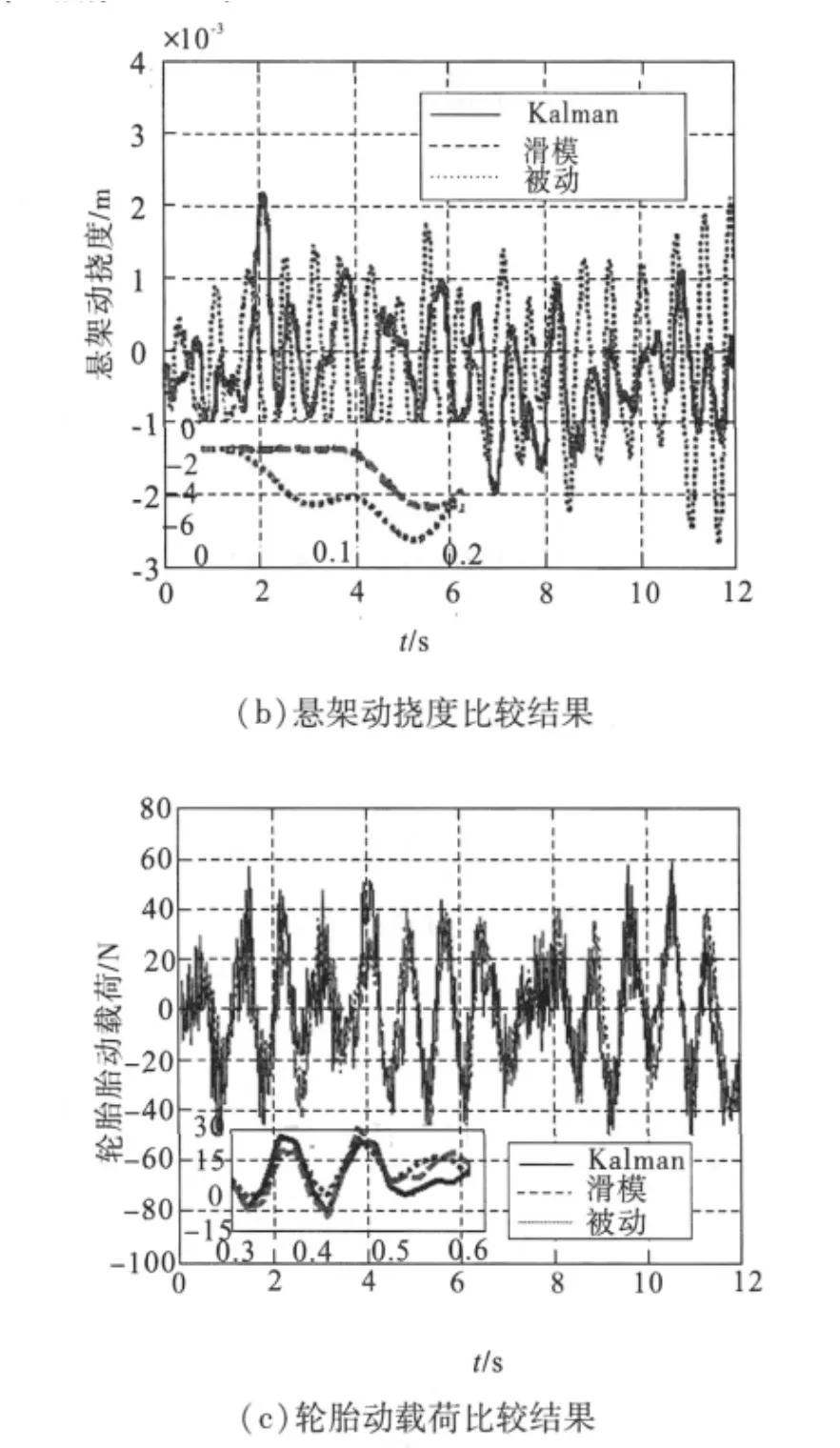
图5 车身加速度、悬架动扰度及轮胎动载荷比较结果
4 结论
本文设计了滤波器重构系统的状态,并用这个重构的状态来代替系统的真实状态来实现所需的状态反馈,探讨了基于Kalman滤波器以及滑模观测器的天棚控制算法,从仿真结果上可以看出Kalman滤波器以及滑模观测器可以较为精确的对系统进行状态估计。此外,还可以得出,相比于Kalman滤波器,滑模滤波器能更好地克服一般状态观测器受到的非线性、参数变化以及干扰等因素的影响,在悬架绝对速度、相对速度的观测上都比Kalman滤波器更加接近实际值。基于观测器的“天棚”阻尼控制方法较被动悬架的振动加速度明显减弱,说明天棚阻尼控制可以提高汽车的平顺性,它为进一步的实车试验研究打下了基础。
[1]姚嘉凌,蔡伟义,陈宁.汽车半主动悬架系统发展状况[J].汽车工程,2006,28(3):276 ~280.
[2]D.Karnopp,M.Crosby,and R.Harwood,Vibration Control UsingSemi-Active Force Generators,Transaction of the ASME Journal ofEngineering for Industry,vol.96,pp.619 ~626,1974.
[3]Hsu Ling-Yuan,Chen Tsung-Lin.Vehicle Full-State Estimation and Prediction System Using State Observers[J].IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY,JUL 2009,58(6):2651-2662.
[4]Hsu Ling-Yuan,Chen Tsung-Lin.Estimating Road Angles With the Knowledge of the Vehicle Yaw Angle[J].JOURNAL OF DYNAMIC SYSTEMS MEASUREMENT AND CONTROL-TRANSACTIONS OF THE ASME,MAY 2010,132(3).
[5]Sharma K Crolla,D.A.D.A.Wilson.The design of a fully active suspension systemincorporating a Kalman filter for state estimation[P].No.389.IEEE Control'94,Conference Publication,344~349.
[6]Raghavan,S.and J.K.Hedrick,J.K.,Observer design for a class of nonlinear systems. International Journal of Control,1994,59,515~528.
[7]Misawa,E.A.and Hedrick,J.K.,Nonlinear observers-a state of the survey[J].AMSE Journal of Dynamic Systems Measurement and Control,1989,111:344 ~352.
[8]R.K.DIXIT and G.D.BUCKNER.Sliding mode observation and control for semiactive vehicle suspensions[J].Taylor& Francis./Vehicle System Dynamics,2005,43(2):83 ~105.
[9]Henry,R.R.and Zeid,A.A.,A nonlinear sub-optimal.observerbased control for semiactive suspension[J].Transactions of the ASME ,Transportation Systems,Dynamic Systems and Control Division,1992,44:181~189.

