浅水分潮对海岸潮致地下水波动特征的影响

楼悦安，宋志尧，孔 俊，程 晨，徐福敏

(1.中国人民解放军92250部队，浙江舟山 316041;2.南京师范大学虚拟地理环境教育部重点实验室和大规模复杂系统数值模拟江苏省重点实验室，江苏南京 210023;3.河海大学港口海岸与近海工程学院，江苏南京 210098)

海岸带是大陆和海洋的过渡地带，受到大气圈、水圈、岩石圈和生物圈等的共同作用，丰富的自然资源和良好的环境条件使之成为人口最为稠密、经济最为发达的地区，在自然与人为灾害因素的作用下，海岸带已逐渐成为各种环境灾害频繁发生、叠合发展的地带，如洪涝、风暴潮、海岸侵蚀、海水入侵、污染等，是典型的生态脆弱带［1］。

我国拥有漫长的海岸线，随着沿海地区社会经济的不断发展，使得因全球变暖而引发的海岸环境灾害有进一步加剧的趋势。已有的研究成果表明，海岸侵蚀、海水入侵及海岸污染等环境灾害几乎都与地下水运动有关，海岸潮致地下水波动的研究已日益为国内外学者所关注［2-8］，并形成了海滩地下水动力学的研究方向［9］。

Jacob［10］基于垂直滩面、顺直岸线、单个承压含水层中的一维流动，忽略非线性效应、毛细效应、垂向流等影响，海潮边界条件为具有一定振幅的余弦函数的假设，与1950年首次提出了描述潮波在承压潜水层传播的最简解析解。由于Jacob解基于上述的严格假设，因此滩面的坡度、岸线的形态特征及组成波的非线性作用等因素都可能造成Jacob解的不适用［11］。Dagan［12］针对垂直滩面，基于非线性地下水控制方程，采用摄动法得到了小振幅波情况下的地下水波动一阶摄动解。Parlange［13］在此基础上进一步推出了二阶摄动解，并指出方程的非线性项在传播过程中产生了高频波动。Nielson［14］考虑了斜坡的影响，推导出了相应的摄动解，并与现场实测数据进行了比较分析。其后Li［15］引入等效边界条件，采用摄动法得到了二阶摄动解。但由于其采用的摄动参数与岸滩坡度有关，而摄动参数又要求小于1，所以该解不适用于缓坡情况。Teo等［16］综合考虑方程的非线性和斜坡的影响，运用双摄动参数，获得了更高阶的摄动解。理论上，摄动参数避免了坡度的影响，但由于长期项的存在，解的精度实际也只能够保留至二阶。对此，Kong et al［17］运用新的双摄动参数，提出基于待定系数的新解析方法，获得了斜坡海岸情况下非线性方程的高阶摄动解，避免了长期项的出现，使摄动解在理论上可推至更高阶。

上述摄动解的推导往往基于单个分潮的假设。Li［15］曾通过两个半日潮研究过大小潮对海岸潜水层地下水波动的影响，指出大小潮引起的地下水波动比由单个半日潮引起的地下水波动向内陆传播更远的结论。实际上，海岸潮汐是十分复杂的，往往由多个分潮共同作用，其中浅水分潮作用显著，所以考虑分潮及其浅水分潮综合影响下的摄动解具有实际意义，但迄今尚无学者研究浅水潮波非线性作用产生的倍潮波即浅水分潮的影响。

为此，主要研究半日潮产生的浅水分潮对海岸潜水层地下水波动的影响，应用在处理地下水问题时常用的摄动法得到了包含半日潮M2和浅水分潮M4综合影响下的地下水波动二阶摄动解，并与现场实测数据和数值解进行了比较，分析了考虑浅水分潮后海岸潮致地下水波动特征的变化。

1 控制方程

针对一维海岸地下水运动，考虑半无限潜水层，底板水平不透水，不考虑毛细管压力对地下水波动的影响，介质单一均质，忽略垂向流动，水位波动幅度相比于潜水层厚度较小(见图1)，得到一维线性Boussinesq方程:

式中:h*(x*，t*)为相对于平均海平面的水位高度(m)，x*为水平方向坐标(m)，t*为时间(s)，z*为垂向坐标(m)，D为平均含水层厚度(m)，K为介质的渗透系数(m/s)，ne为有效孔隙度。

图1 海岸潜水层潮致水位波动示意Fig.1 Sketch map of tide-induced groundwater fluctuations in coastal aquifer

在外海潮汐作用影响下，x*→∞时向陆一侧水位梯度为0，即

为考虑浅水分潮对地下水波动的影响，假设外海潮汐过程为

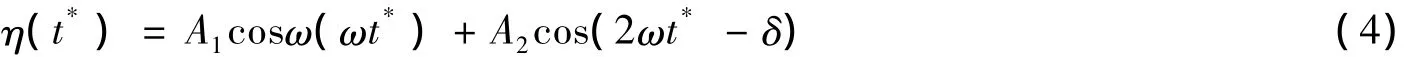
其中，A1，A2分别为分潮M2，M4的振幅(m)，ω为分潮M2的角速度(rad/h)，δ为分潮M2与其浅水分潮M4之间的相位差(rad)。

引入新变量z*=x*-(t*)，将动边界问题转化为固定边界问题，代入式(1)，并记r=A2/A1，得到的方程可写为以下形式:

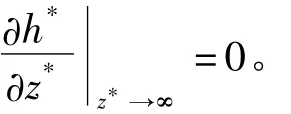
2 二阶摄动解

以ε为摄动参数，可设式(6)的摄动解:

应用Li［15］相同的方法，可解得二阶摄动解为

显然，当r=0时，上述二阶解可退化为Li［15］的解。

3 解的验证

3.1 现场观测

2010年7月1日至7月15日在苏北弶港附近的潮滩区进行了一次现场观测，潮滩剖面及测井布置如图2所示。

图2 测井布置Fig.2 Sketch map of arranged observation wells

弶港位于120°51'E，32°44'N，该海域潮汐变化显著，外海属正规半日潮，潮差最大超9 m，而近岸水深变浅，潮差减小，但浅水分潮作用显著，主要是半日潮及其浅水分潮;同时海滩地质组成较单一，斜坡平缓，潜水层较浅，非常适合研究半日潮及其浅水分潮对地下水运动的影响。观测仪器主要是测量水位的回声探测器仪，测程0～12 m，精度0.1 cm，可自动记录。根据闸外航道潮汐特征，测井长度为4 m，滩面最深处入土2.5 m。

各测井的地下水水位测量从7月1日上午08∶30开始，间隔为10 min;潮汐水位从7月6日15∶00开始观测，间隔为1 h。

由图3可以看出，各测井地下水位随着潮汐水位的变化而变化。各测井地下水位的波动过程线具有非对称性，水位上涨过程要明显陡于下落过程，Knight［18］指出这是由于在涨潮过程中孔隙的透水性要明显高于落潮造成的。各测井地下水位的波动振幅沿程减小，这是由于传播过程中的能量耗散造成的;同时沿程各测井出现了相位滞后的现象，这是因为波动传播过程阻尼作用导致的。

图3 潮汐水位及各测井地下水位变化过程(基面为85高程)Fig.3 Time series of groundwater fluctuations in each well and tide level(85 datum)

3.2 潮汐边界条件

为了充分研究浅水分潮对潮致地下水波动的影响，利用上述现场观测数据中的某一天(2010年7月9日08:00至次日08:00)进行研究分析。

由于海岸实测潮位的观测时间短，且有效时段更短，不宜应用常用的调和分析方法分离各分潮，为此，假定海岸潮位为

式中:h0为平均海平面高度(m);hM2，hM4分别为分潮M2及其浅水分潮M4的振幅(m);φ1，φ2分别为分潮M2，M4的初相位(rad)。

对表达式(7)，应用简单实用的最小二乘法进行拟合，最终可得到h0=1.05 m，hM2=1.33 m，hM4=0.49 m，φ1=1.86 rad，φ2=3.30 rad。所以由分潮M2及其浅水分潮M4引起的闸外潮汐水位变化表达式为

图4为预测水位与实测水位的拟合情况。由图可以看出，两者拟合良好，可以作为这里研究的海岸潮汐边界条件。

图4 实测水位与预测水位拟合ig.4 Tide level fitting result between observation and prediction

3.3 结果比较

选取在同一坡面上的1、2、4、5号测井的实测数据与摄动解及数值解进行比较分析。相关参数分别为:A1=1.33 m，A2=0.49 m，K=29.0 m/d，ne=0.5，tan(β)=0.20，D=5.0 m，δ= φ2-2φ1=-0.42 rad。

由图5比较摄动解、数值解和实测值，可以看出:1)对于某一测井来说，波动振幅随着摄动解阶数的增加与实测值愈接近，由于高阶摄动解越趋复杂，一般只能推导至二阶解，如果推至三阶甚至更高阶的解，摄动解与实测值应该越来越接近。当然，在水位谷值处，摄动解与实测值之间还可能存在较大的偏差，这主要是由于坡面溢出点的形成造成的，此时作为潮致地下水运动控制方程的边界条件已发生了根本的变化，涨潮时临海一侧地下水头为潮汐水位，而落潮时由于潜水层内落潮较慢，溢出点与潮汐水位不再同步(如图1)。同时数值解相比二阶解具有更高的精度，与实测值也更为接近;2)1号测井由于最靠近外海，所以由摄动解反映的地下水位波动过程线与实测地下水波动的相位基本一致，而2、4、5号测井由摄动解反映的地下水波动相比实测地下水位过程线会整体向右略有偏移，这主要是由于摄动解是在十分概化的条件下获得的，如斜坡坡度是规则的、潜水层是等厚度的、介质参数(渗透系数和孔隙度等)是均匀的等等，又没有考虑溢出面、垂直流、毛细作用及组成波的相互作用等的影响，造成计算的波长要比实际波长偏大。这一现象与Nielson［14］的研究结果基本一致。而数值解较二阶摄动解在相位偏移上有一定程度的改善。综上所述，各阶摄动解基本上能反映海岸潮致地下水波动的趋势性特征，摄动解的阶数越高，其所反映的波动特征越充分。

图5 各测井各阶摄动解与数值解及实测过程线比较(相对于平均海平面)Fig.5 Time series comparison of perturbation solutions，numerical results and observed data in each well(relative to averaged sea level)

需要强调的是，即使采用实测的边界潮位进行数值模拟，计算值与实测值在潮致地下水波下落过程的后期仍存在一定的误差，表明目前常用的Boussinesq方程，是基于潜水层等深和介质参数(渗透系数和孔隙度等)是均匀的等假定条件得到的，又没有考虑溢出面、垂直流、毛细作用等的影响，所以只能反映海岸潮致地下水波动的基本特征，如超高、振幅和相位等。由于这里只是讨论浅水分潮对这些基本特征的影响，而且这种影响也是相对的，因而基此进行分析研究目前仍是可行的。

4 分析讨论

为了研究浅水分潮对海岸地下水波动基本特征的影响，将从超高、振幅、相位等潮致地下水波动特征进行比较分析。

4.1 超高

在潮汐作用下，海岸潜水层内的平均地下水位会产生相对于平均海平面的雍高。当沙滩倾角较小时，这种由于潮汐作用而产生的超高非常明显。同时地下水超高也是海岸地下水波动非线性作用的一个基本特征。Philip［19］和Smiles［20］曾基于一维非线性Boussinesq方程计算了直墙海岸内的地下水超高;Parlange在其二阶摄动解和实验的基础上对地下水位超高进行了分析，证实了潮致地下水水位超高的存在。根据之前获得的二阶摄动解，在周期平均后，忽略其中的周期项，得到地下水超高沿程二阶解析解:

相应不考虑浅水分潮的解即Li的解反映的地下水超高沿程变化:

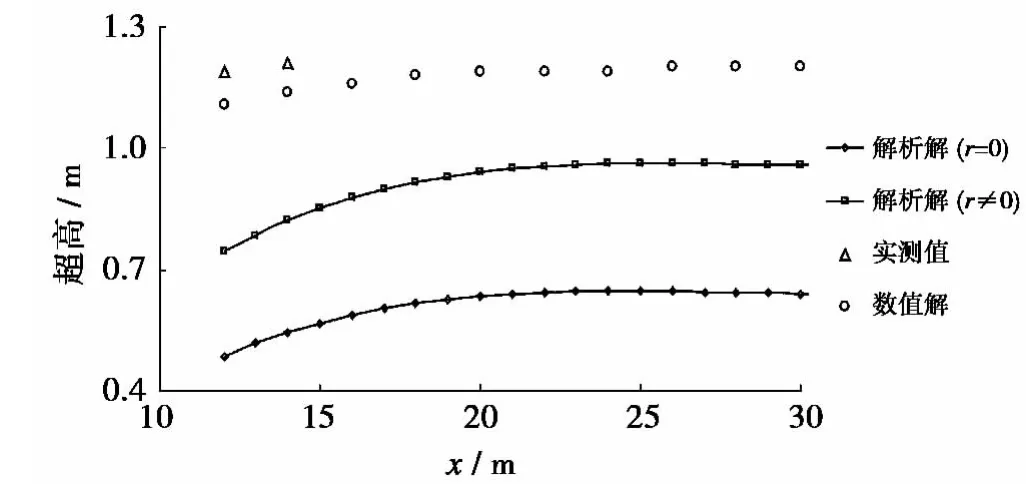
图6 超高沿程分布比较Fig.6 Comparison of water table over-heights along inland direction

1、2号测井由于会被海水淹没，所以其分析计算得到的超高值并不能真实反映其本质特征。选取离外海较远的4、5号测井的实测超高与解析解及数值解进行比较(见图6)。考虑浅水分潮后，解析解反映的地下水位超高有了明显的提升，但是与实测地下水位超高还是存在一定的差值。一方面是由于忽略了方程自身的非线性作用;另一方面是由于在水位谷值处摄动解与实测值之间存在一定的偏差。而数值解反映的地下水位超高相比解析解要更接近实测值。由此可知，如果忽略浅水分潮的影响将会极大地低估地下水位超高值。

4.2 振幅

图7为两种不同情况下二阶摄动解、数值解与1号测井的实测值过程线的比较图。

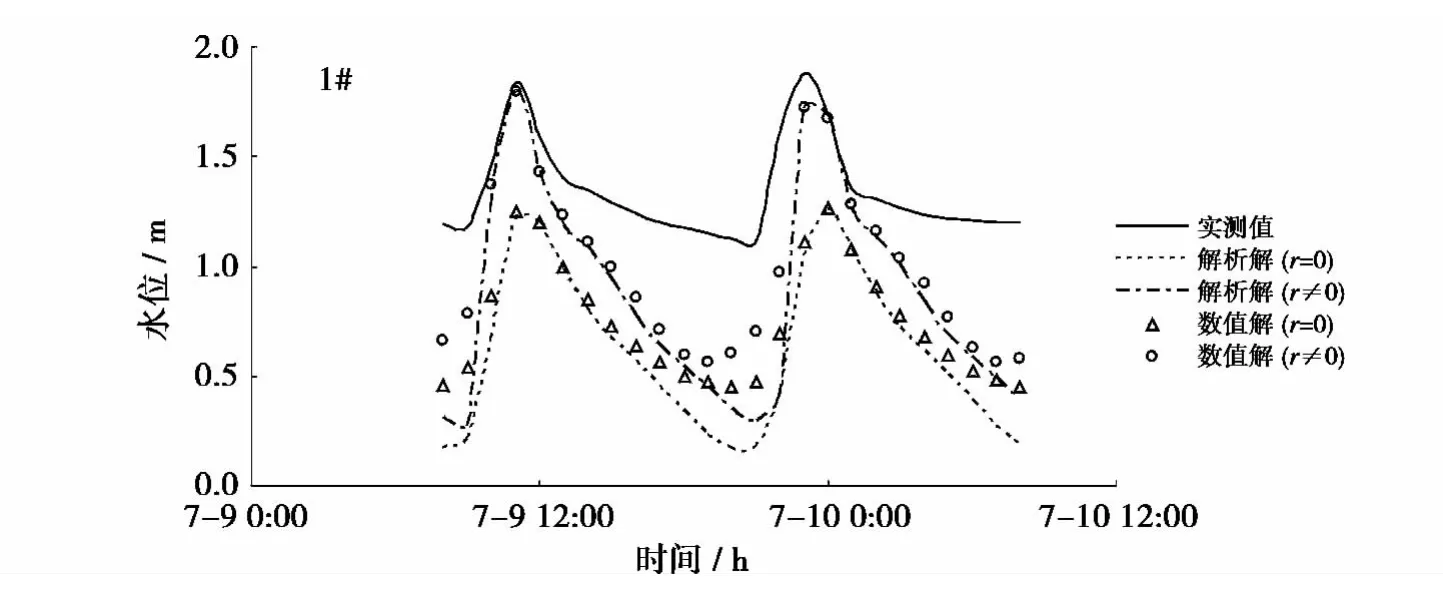
图7 不同情况下二阶摄动解、数值解与实测过程线比较Fig.7 Time series comparison of second-order perturbation solutions，numerical results and observed data in No.1 well

4.3 相位

同样由图7可以看出，仅考虑半日潮M2的摄动解反映的地下水位波动曲线较之实测地下水位波动曲线存在向右偏移的趋势，而考虑浅水分潮M4后的摄动解反映的地下水位波动曲线与实测地下水位波动曲线的相位基本一致。这表明，考虑浅水分潮后可以在一定程度上改善摄动解与实测值之间的相位偏离。

5 结语

针对浅水分潮M4对海岸潮致地下水波动特征的影响进行了研究。通过对考虑浅水分潮M4后的二阶摄动解与实测值的比较可以看出，两者之间的峰值较为吻合，但因目前研究所应用的控制方程即Boussinesq方程忽略了溢出面、垂直流、毛细作用等因素，包括数值解在内计算的谷值误差仍较大;同时对某一测井来说，摄动解阶数越高，越能充分反映地下水波动特征，相对而言数值解能较好地反映实测的潮致地下水波动特征。概括地说，浅水分潮对潮致地下水波动的振幅及其超高值有较显著的影响，由于斜坡的非线性作用，这种影响明显大于海岸边界浅水分潮与半日潮的振幅比;同时可较好地改善相位上出现的偏移，表明在研究海岸潮致地下水波动特征时浅水分潮作用是不能忽略的。

［1］ 施雅风.我国海岸带灾害的加剧发展及其防御方略［J］.自然灾害学报，1994，3(2):3-14.

［2］ Chappell J，Eliot I G，Bradshaw M P.Experimental control of beach face dynamics by water table pumping［J］.Eng.Geol.，1979，14:29-41.

［3］ Fragoso G，Sepencer T.Physiographic control on the development of spartina marshes［J］.Science 322，2008，1064.

［4］ Pinder G F，Cooper H H.A numerical technique for calculating the transient position of the saltwater front［J］.Water Resources Research，1970，6(4):875-882.

［5］ 薛禹群，谢春梅，吴吉春.海水入侵研究［J］.水文地质工程地质，1992，19(6):23-33.

［6］ 蔡祖煌，马凤山.海水入侵的基本理论及其在入侵发展预测中的应用［J］.中国地质灾害与防治学报，1996，7(3):1-9.

［7］ Moore W S.Large groundwater inputs to coastal waters revealed by 226Ra enrichment［J］.Nature，1996，380(18):612-614.

［8］ 贾国东，黄国伦.海底地下水排放:重要的海岸带陆海相互作用过程［J］.地学前缘，2005，12(特刊):29-35.

［9］ Horn D P.Beach groundwater dynamics［J］.Geomorphology，2002，48:121-146.

［10］ Jacob C E.Flow of Groundwater in Engineering Hydraulics［M］.New York:［s.n.］，1950:321-386.

［11］ Trefry M G，Johnston C D.Pumping test analysis for a tidally forced aquifer［J］.Ground Water，1998，36(3):427-433.

［12］ Dagan D.Second-order theory of shallow free-surface flow in porous media［J］.The Quarterly Journal of Mechanics and Applied Mathematics，1967，20(4):517-526.

［13］ Palange J Y，Stagnitti F，Starr J L，et al.Free-surface flow in porous media and periodic solution of the shallow-flow approximation［J］.Journal of Hydrology，1984，70(1-4):251-263.

［14］ Nielsen P.Tidal dynamics of the water table in beaches［J］.Water Resources Research，1990，26(9):2127-2134.

［15］ Li L，Barry D A，Stagnitti F，et al.Beach water table fluctuations due to spring-neap tides:moving boundary effects［J］.Adv Water Resour，2000，23(8):817-824.

［16］ Teo H T，Jeng D S，Seymour B R，et al.A new analytical solution for water table fluctuations in coastal aquifers with sloping beaches［J］.Adv Water Resour，2003，26(12):1239-1247.

［17］ Kong J，Song Z Y，Xin P，et al.A new analytical solution for tide-induced groundwater fluctuations in an unconfined aquifer with a sloping beach［J］.China Ocean Eng，2011，25(3):479-494.

［18］ Knight J H.Steady period flow through a rectangular dam［J］.Water Resources Research，1981，4(17):1222-1224.

［19］ Philip J R.Periodic nonlinear diffusion:An integral relation and its physical consequences［J］.Aust J Phys，1973，26:513-519.

［20］Smiles D E，Stokes A N.Periodic solutions of a nonlinear diffusion equation used in groundwater flow theory:Examination using a Hele-Shaw model［J］.Journal of Hydrology，1976，31(1-2):27-35.