面向地形匹配的多波束测深数据抽稀方法研究

訾桂峰，程秀丽，刘 毅，徐遵义

(1.潍坊市科学技术情报研究所，山东潍坊 261061;2.山东建筑大学计算机科学与技术学院，山东济南250101)

水下地形定位技术有可能解决水下潜航器长时间高精度导航定位问题，已成为新型导航系统发展的重要方向，其中基于多波束系统的地形辅助导航更成为研究和发展的重点［1-2］。由于多波束测深的高精度和高密度导致实时获得的数据量巨大，必须对其进行重采样才能用于海底地形辅助导航，其中数据抽稀是实现重采样算法的主要步骤之一［3-4］。

目前多波束测深数据抽稀算法主要有两类:基于非散乱数据的数据抽稀算法和基于二维散乱数据的数据插值方法。前者代表性的算法主要有基于格网的数据抽稀和基于系统的抽稀［5-6］，该类算法的主要特点是运算速度快，主要用于多波束数据的快速显示，多波束测深系统自带软件多采用此类算法，但因对多波束测深数据模型过分简化而导致精度低，很多地形特征点无法保留;后者代表性的算法主要有基于邻近距离及高差的抽稀算法和基于不规则三角网的抽稀算法［7-9］，该类算法能有效保留地形特征点，抽稀精度高，但运算量巨大，无法实时执行，多用于多波束测深数据的后期离线处理和地形可视化。面向地形匹配的多波束测深数据抽稀算法需要在运算速度、采样密度和精度之间达到一种最优平衡，因此结合已有两类抽稀算法的优点，对多波束测深每ping数据采用角度-弦高联合准则法进行抽稀处理，对多ping抽稀后的数据基于点云离散度再进行简化，从而实现用于地形匹配的多波束测深数据抽稀。

1 抽稀算法及实现

面向海底地形导航定位的多波束测深数据抽稀方法包括基于角度-弦高的每ping数据抽稀和基于点云离散度对多ping实测数据的抽稀处理。

1.1 角度-弦高联合准则抽稀法

在相邻点水深差距较大时，即使夹角很小，弦高也可能很大;当在相邻点水深差距较小时，即弦高很小，角度也可能很大，如图1所示。因此同时使用角度和弦高2种误差限对水深数据进行判别，凡是水深点同时小于2种误差限的点舍去。基于角度-弦高联合准则的数据抽稀算法首先给定角度误差限Δα和弦高误差限Δd，然后对数据逐点进行判断，算法步骤［10］:

1)给定阈值Δα和Δd;

2)从起始点开始取相邻的测深点P0，P1，P2;

3)对于 P0，P1，P2，计算P0P1到P0P2的夹角 α 和d=|P0P1|sinα;

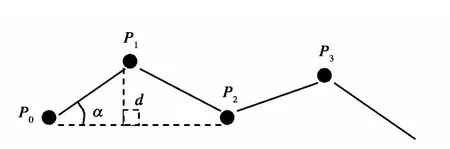
图1 角度和弦高示意Fig.1 Angle＆chord height of polygonal line

4)若α＜Δα并且d＜Δd成立，则舍去测深点P1，取P2后的一点P3;若P3不存在，则表明该ping测深数据已处理完毕，转第6)步;若P3存在，则置P1=P2，P2=P3，转第3)步;

5)若α＜Δα并且d＜Δd不成立，则置P0=P1，P1=P2，取P2后的一点P3;若P3不存在，则表明该ping测深数据已处理完毕，转第6)步;若P3存在，则置P2=P3，转第3)步;

6)判断是否所有ping均已取完，如果没有则取下一ping数据，转第2)步，否则算法结束。

多波束测深获得的数据是按ping存储的，每ping可接收数百个水深数据(如Simrad EM3002最多可接收508个水深数据)，这些水深数据基本上位于同一条曲线上，对于每ping数据采用角度-弦高联合准则，利用给定的角度和弦高误差来对每ping测深数据进行抽稀处理。

1.2 基于点云离散度的抽稀方法

对于海底某一地形区域，水深高程差异的大小表现为地形起伏程度的高低。为了有效地描述水深差异与地形起伏的关系，采用离散度的概念进行阐述。

离散度定义:对于大小为MXN的某块地形区域，设Z［i，j］是水下地形某点的测深值，¯Z为该区域所有点的水深平均值，则局部区域中该点的离散度可定义为［11］

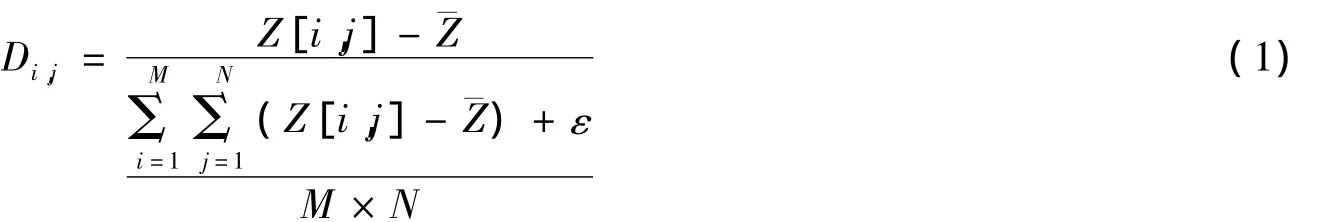
式中:Di，j为点云的离散度，ε为一很小的正数，用于防止平坦区域水深值完全相同时公式分母为零的情形。

点的离散度反映了该点对区域地形起伏贡献的程度。利用点云的离散度可探测点云对地形起伏的影响程度，在简化过程中可提取那些对地形起伏贡献较大的点予以保留，从而保持测区的地形起伏特征。基于点云离散度的抽稀算法步骤:

1)根据多波束回波数、海底地形图水深和惯导指示位置确定条带宽度，根据载体运行速度和采样间隔确定条带长度，根据导航地形图格网大小对实测数据进行格网划分;

2)根据海底地形图水深精度和位置精度生成水深差阈值和地形点最小距离阈值;

3)对给定格网中的所有点按水深值进行排序，若格网中点的水深最大值与最小值之差大于水深差阈值，则视最大、最小值点为地形特征候选点作保留标志;

4)计算格网中其它点的离散度，离散度大于阈值的则作保留标志;

5)确定当前格网的索引号，搜索近邻区域，对于邻域中距离当前格网候选特征点较近而且水深差小于阈值的作删除标志;

2 抽稀算法精度评估方法

参考空间曲面形态参数和空间关系，采用抽稀前后空间曲面表面积的改变和抽稀前后DEM的误差来定量表示以及等值线图定性表示。

空间曲面表面积的计算采用构成曲面的三角形格网表面积的和来计算，如图2所示。空间三点P1，P2，P3构成的三角形上的曲面面积［12］:

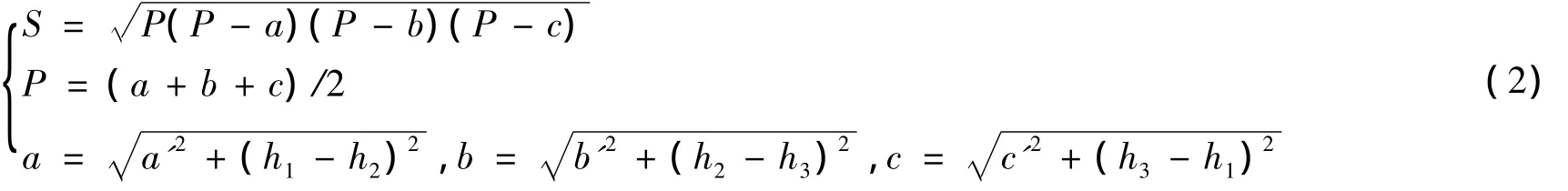
式中:h1，h2，h3为数据点 P1，P2，P3上的数据值;a'，b'，c'为 ΔP1P2P3的边长。

由于抽稀前后测深数据只是在数量上有所减少，数值本身并未改变，因此采用内插点云的方式计算抽稀前后构成的DEM误差，对于内插方法采用改进的Shepard方法。首先均匀地从原始采样数据中抽取N个点将其水深值作为真值，然后用抽稀后的结果点云内插出这N个点的水深值并比对真值，最后统计抽稀前后的误差指标。误差指标采用最大绝对误差MAE、中误差RMSE和平均差ME来度量。

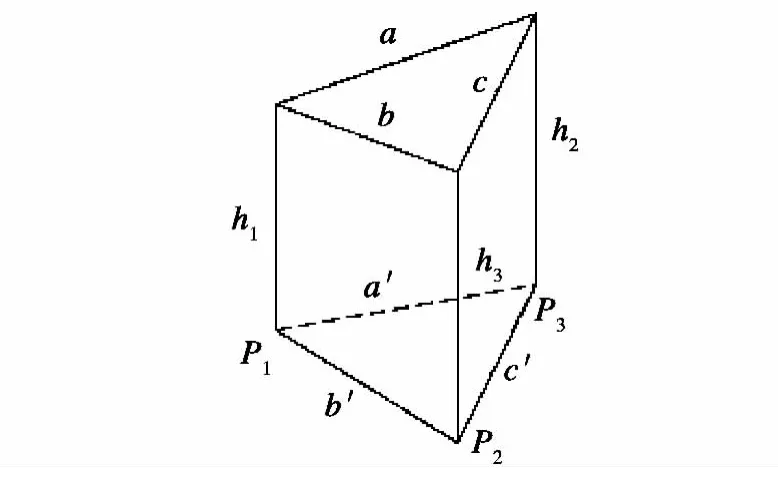
图2 三角形格网曲面面积Fig.2 Surface area of triangulated network

3 数据抽稀实验与结果分析

为了评估提出的多波束测深数据抽稀算法的精度及其对实际地形的适用性，选用数学曲面和实际地形进行了试验。

3.1 基于数学仿真曲面数据的实验分析

为了检验数据抽稀算法对各种地形的适用性，选用椭圆抛物面(模拟谷底)、马鞍面(模拟山脊及鞍部)、高斯曲面(模拟山峰的起伏)等能模拟代表性特征地形的可调节参数曲面来对抽稀算法进行评估。

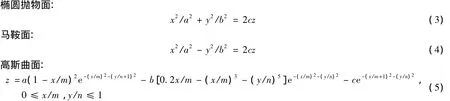
实验曲面的参数取值:a=3，b=10，c=1/3，m=n=1。

为了使数学仿真生成的曲面数据更加符合多波束实际，分别对位置数据增加格网间距1% 、水深数据增加水深值1% 的高斯误差，曲面采用Delaunary三角形构造，原始曲面加误差后形成的条带数据(以下简称仿真条带数据)及其经抽稀后形成的曲面分别如图3和图4所示。仿真条带数据抽稀前后数据点数、Delaunary三角形数量以及离散点抽稀率、抽稀前后Delaunary三角形面积变化率如表1所示(角度10°，弦高:每ping水深均值10%，离散度阈值:格网内水深均值150%);三种仿真曲面DEM误差如表2所示。

图3 仿真条带数据曲面Fig.3 3-D image of simulated swath data

表1 三种仿真曲面抽稀效果Tab.1 Thinned results of simulated surfaces data

图4 仿真条带数据抽稀后数据曲面Fig.4 3-D image of simulated swath thinned data

表2 三种仿真曲面DEM误差Tab.2 DEM errors of simulated surfaces thinned data

由图3和图4以及表1和表2可知，提出的数据抽稀算法对三种典型地形均具有很好的抽稀效果，数据抽稀率均在85%以上，抽稀前后曲面表面积变化率均小于3%，其中椭圆抛物面点云数据抽稀率最低，高斯抛物面抽稀率最高。原因在于椭圆抛物面均匀变化，需要保留较多的点反应原曲面，高斯曲面平面部分较多，而平面可以用较少的点来表示，但高斯曲面变化部分变化剧烈，导致抽稀前后曲面误差较大，与表2高斯曲面DEM误差最大相符合。马鞍型曲面介于椭圆抛物面和高斯曲面之间，其数据抽稀率和DEM误差也介于二者之间，但其抽稀后重构曲面与原仿真曲面变化最大，原因在于马鞍型曲面变化的不规则性。

3.2 基于实测数据的实验分析

为了验证文中提出的抽稀算法对实际地形的适用性，在此随机选用2条多波束实测条带数据的一部分进行抽稀实验，抽稀结果如表3所示 (角度10°;弦高:每ping水深均值10%;离散度阈值:格网内水深均值150%)，其中第2块条带数据抽稀前后三维效果如图5所示。

表3 实测多波束地形数据抽稀结果Tab.3 Thinned results of surveyed terrain data

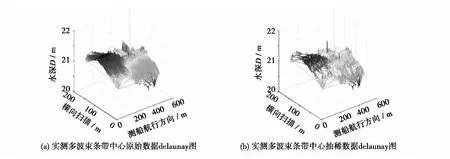
图5 实测多波束数据抽稀效果Fig.5 Comparison between surveyed terrain data and thinned terrain data

由表3和图5可知，提出的数据抽稀方法对多波束实测地形数据比仿真曲面数据有更好的抽稀效果，原因在于水下实际地形变化平稳，剧烈变化的地形较少，可以用更少的点来表示原先的点云数据，减少数据存储以及为后期测深数据的处理提高效率。

为了考察提出的多波束数据抽稀算法与已有多波束数据抽稀算法的在运算速度、抽稀精度等方面的差异，对实测条带数据1进行了对比试验。试验环境:笔记本电脑 Dell Inspiron 1440(CPU T6600 2.2 GHz，RAM 4GB)，MS Windows Server 2003企业版，Matlab 2010a，传统抽稀算法采用基于格网的数据抽稀算法(用格网均值代表格网值)和邻近距离及高差［7］(邻近距离采用格网外接圆，高差采用邻近区域水深均值10%)，精度评价在前述评价方法的基础上增加算法运行时间，实验结果如表4所示。

表4 实测多波束地形数据1不同抽稀算法运行结果Tab.4 Experiment results of different thinning algorithms of first surveyed terrain data

由表4可知，这里提出的多波束数据抽稀算法数据抽稀率和精度与基于邻近距离及高差的数据抽稀算法接近，算法运行时间与基于格网的数据抽稀算法接近，因此这里提出的该算法具有较高的精度以及实时性较好，能比较好地适用于面向地形匹配的数据重采样应用。

4 结语

当多波束测深数据用于水下地形辅助导航定位时，数据实时抽稀处理需考虑以下问题:1)多波束测深系统的波束数、水深和载体运行速度，它们决定了多波束测深条带的面积;2)算法对于任意地形区域都能得到较好的结果，并不具有特殊性;3)算法应简洁，执行效率高，为此算法要特别关注海底地形特征点特征。

这里将角度-弦高准则与点云离散度抽稀方法相结合用于多波束地形数据抽稀处理，通过仿真曲面和多波束实测地形数据实验验证，获得以下结论:

1)角度-弦高准则与点云离散度抽稀方法相结合可以实现对多波束测深数据的实时抽稀，点云离散点抽稀率仿真曲面在85%以上，实测数据在90%以上;

2)角度-弦高准则用于多波束每ping数据的抽稀，点云离散度用于多 ping组成的曲面数据的抽稀，算法充分利用了多波束水深测量的特点，算法实时性较好;

3)通过对每ping数据的抽稀和对多ping数据的联合抽稀，这种抽稀方法能很好地保留测深数据的几何特征，同时又可以获得较高的抽稀率。

在数据抽稀过程中，角度、弦高以及点云离散度阈值均为经验值，算法在普适性上还存在一定的问题，同时针对不同地形应该采用不同的格网划分和不同的阈值，这是今后进一步要研究的主要内容。

［1］ 王杰华.国外各种导航定位技术最新进展［J］.中国航天，2010，8:30-34.

［2］ 李 临.海底地形匹配辅助导航技术现状及发展［J］.舰船电子工程，2008，28(2):17-19.

［3］ 于家城，陈家斌，贺 鹏，等.基于FFT的海底地形二维匹配技术［J］.系统仿真学报，2008，20(21):5795-5797.

［4］ 马 妍.基于多波束测量数据的海底地形可导航性分析［D］.哈尔滨:哈尔滨工程大学，2010.

［5］ 夏 伟，黄谟涛，刘雁春，等.Douglas-Peucker算法在多波束测深数据抽稀中的应用［J］.测绘科学，2009，34(3):159-161.

［6］ 曹鸿博，张立华，朱穆华，等.海量多波束数据抽稀方法的比对分析［J］.海洋测绘，2010，30(5):81-83.

［7］ Pamela S.A data density reduction algorithm for Post-processed airborne lidar bathymetric survey data［D］.Florida:University of Florida，2000.

［8］ 马建林，金 菁，来向华.多波束测深海底数字地形模型的建立［J］.海洋测绘，2005，25(5):15-17.

［9］ 贾俊涛，翟京生，孟婵媛，等.基于海量多波束数据的海底地形模型的构建与可视化［J］.测绘科学技术学报，2008，25(4):255-259.

［10］洪 军，丁玉成，曹 亮，等.逆向工程中的测量数据精简技术研究［J］.西安交通大学学报，2004，38(7):661-664.

［11］徐景中，万幼川，张圣望.LIDAR地面点云的简化方法研究［J］.测绘信息工程，2008，33(1):33-34.

［12］郭仁忠.空间分析［M］.第2版，北京:高等教育出版社，2004.