基于Asaoka 法的软基沉降量预测研究与应用

程 强，杨丽萍，孙文慧

（1.天津市水利科学研究院，天津 300061；2.天津华水水务工程有限公司，天津 300061；3.天津市引滦工程黎河管理处，河北遵化 064200）

在软土加固的设计、施工工作中，最终沉降量的计算非常重要。在设计中最终沉降量一般采用分层总和法，而分层总和法只考虑了主固结沉降量，无法考虑瞬时沉降和次固结沉降；实际工程中通常是在现场埋设沉降标、板等各种观察仪器，定期观测地面沉降值，该沉降值是瞬时沉降、主固结沉降量和次固结沉降之和，因此两者之间存在差异，如何通过已有沉降资料推算实际工程最终沉降量就显得非常重要。Asaoka于1978年提出了一种新的推求最终沉降量方法，笔者以温州某软基处理工程现场测试数据为依据，对该法推求最终沉降的影响指标进行了分析探讨。

1 Asaoka法基本理论

对于一维固结问题，Mikasa的固结微分方程采用应变形式表达如下：

Asaoka提出了一种利用一段时间沉降观测资料来预计最终总沉降量和沉降速率的新的实用计算方法。Asaoka认为，以体积应变表示的一维固结方程可近似地用一个级数形式的微分方程表示：

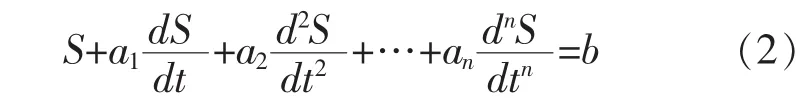
式中：S为总固结沉降量（包括瞬时沉降、主固结沉降和次固结沉降）， 一般以 mm 计；a1，a2，…，an以及b均为常数，其值取决于固结系数和土层边界条件。

Asaoka法基本思想就是利用己有的沉降观测资料求出这些未知数，然后据此参数预估最终沉降量。根据沉降—时间关系曲线，式（1）可用递推形式表示为：

式中：Sj即 tj时刻的沉降量 （一般以 mm 计），tj=jΔt，Δt为相邻两次沉降观测的时间间隔（一般以d计）；β0为沉降值；βi为无维数的常量。

对于大多数实际情况，通常第一阶近似就足够了，式（2）、（3）可以简化为：

式（4）中的沉降（S）即为待求未知量，由于其本身及导数都是一次的，那么式（4）属于典型的一阶线性非齐次微分方程。设地基的初始沉降量、最终沉降量分别为S0和S∞，则该方程的通解为：

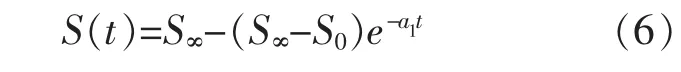
在上式中令t=tj，则当时间tj趋于无穷大时，Sj=Sj-1并且 S（tj）=S∞，代入式（5）可得到最终沉降量：

Asaoka法也叫图解法，如图1所示，其计算步骤如下：

（1）在实测S-t曲线横轴上划分相等的时间段Δt，读出 t1，t2，…，tm所对应的沉降值 S1，S2，…，Sm；

（2）在以 Sj-1，Sj为坐标轴的平面上，将沉降值以点（Sj-1，Sj）画出，同时做出 Sj-1=Sj的直线；

（3）将点（Sj-1，Sj）拟合成为直线，该直线与 Sj-1=Sj直线相交点对应的沉降值为最终沉降量（S∞）。

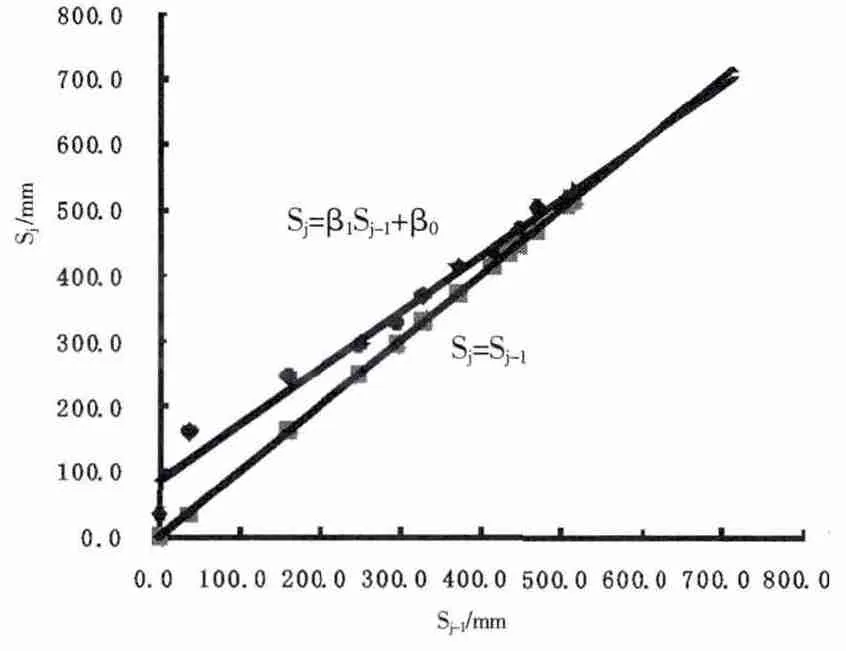
图1 Asaoka法计算简图

2 工程介绍

温州某软基加固工程为规划道路原地基层的加固，采用真空预压法进行加固，场地地基土在加固深度内自上而下分为3个工程地质层 （其中②层细分为2个亚层）：①黏土层，②1含细砂淤泥层、②2淤泥层，③淤泥质黏土层。路基加固采用立体排水系统，塑料排水板为垂直排水通道，波纹盲管为水平排水通道，排水板呈正三角形布置，排水板规格为100 mm×4 mm、间距1.6 m、深度4.2 m，加固区域真空度维持在80kPa以上。

图2给出了该工程加固分区a4、a5满载后6个月时间内的沉降量随时间变化曲线，a4分区加载6个月的沉降量为501 mm，a5沉降量为526 mm，该工程沉降量观测的时间间隔相等，均为3 d。

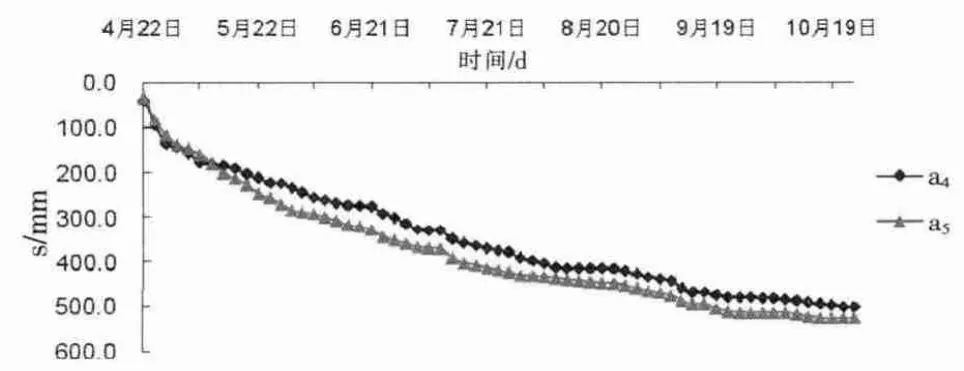
图2 实测沉降-时间曲线

3 Asaoka法预测沉降量

在利用Asaoka法计算最终沉降量的过程中，需要读出相同时间间隔（Δt）的沉降量值，由于该工程是在等时间间隔（3 d）内进行沉降观测，所以当Δt是3的整数倍时，无需对沉降曲线进行抛物插值，读取实际沉降量值即可进行沉降计算；当Δt不是3的整数倍时，须采用数学上的抛物插值计算不同时刻的沉降值。

为了尽量减少抛物插值带来的误差，本工程选取的Δt均为3的倍数，这样可以直接读出实际沉降量值进行计算，减小误差。

3.1 初始沉降值对Asaoka法的影响

初始沉降值通常指的是软土地基加固中前期观测的沉降量，该值的取舍对Asaoka法求解最终沉降量的影响很大，下面以加固分区a4、a5为例作简单介绍 （笔者所取初始沉降值为加载后第一次观测值）。表1为Asaoka法中取舍初始值对斜率及最终沉降量的影响，从中可以分析得出以下结论。

（1）斜率（β1）：无论是保留还是舍去初始值，采用Asaoka法所拟合的直线斜率（β1）都随着时间间隔的增大而减小，但是两者的变化幅度不一样，舍去初始值斜率随时间间隔变化较大，a4从0.911 5减小到0.699 2，a5从0.900 4减小到0.616 1；而保留起始值斜率随时间间隔变化较小，a4从0.914 4减小到0.853 9，a5从 0.909 9 减小到 0.802 5。

（2）最终沉降量（S∞）：取或舍初始值对最终沉降量的计算影响比较明显，同一时间间隔保留初始值所预测的最终沉降量要大于舍去初始值所预测的最终沉降量，两者最小差4.6 mm，最大差208.9 mm；对于舍去初始值所预测的最终沉降结果随时间间隔的变化不大，比较接近，而对于保留初始值预测的结果随时间间隔的变化较大，最大值是最小值的1.5倍，两者相差了247.2 mm。

不论是堆载预压还是真空预压，由于在加载初期软土本身结构会发生一定变化，这部分沉降值往往是不准确的，所以在采用Asaoka法预测最终沉降量时一般会去掉起始值，消除初始值对沉降预测的影响。

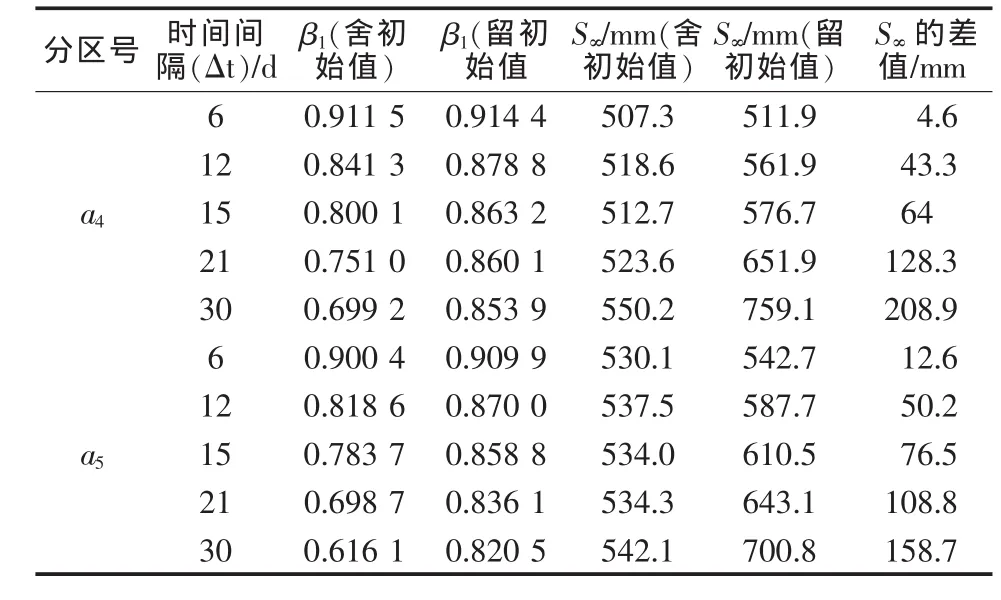
表1 Asaoka法中取舍初始值对斜率及最终沉降量的影响

3.2 最终沉降量计算及分析

表2给出了不同Δt下采用Asaoka法计算最终沉降量的结果以及相关参数。由此可见，Δt的取值对最终沉降量有直接的影响，当Δt较小时（6 d），计算的最终沉降量值较小；当Δt较大时（30 d），计算的最终沉降量值较大。Δt=6 d与Δt=30 d计算所得最终沉降量相差较大，在a4分区中差值为43 mm、a5分区差值为12 mm，这主要是由于当Δt过小时，插值点较多，会造成拟合点的跳跃性较大，拟合结果偏小；当Δt过大时，插值点较少，β1偏小，会产生一定的偏差，拟合结果偏大。在实际的计算中需要取不同的Δt多算几组，然后在这几组中选择相关系数（R）最大的那组作为最终沉降量的结果，可以降低Δt的选取所带来的偏差。根据相关系数标准，可以认为Δt=12 d的沉降预测结果最好。

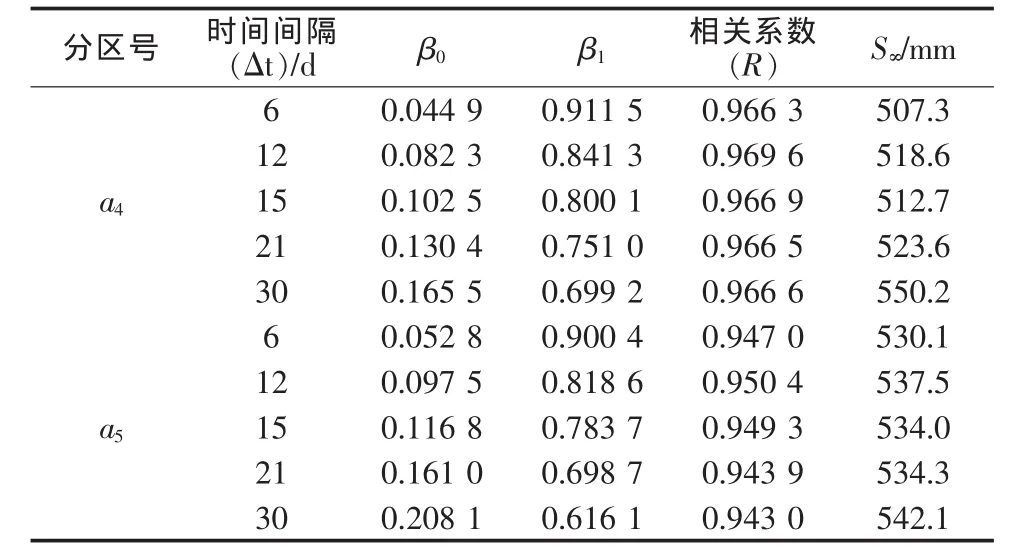
表2 加固分区a4、a5最终沉降预测及相关数据

另外，从表2中可以看出，随着Δt取值的变化，β0、β1也在相应变化，直线斜率（β1）随时间间隔增大而减小，截距（β0）随时间间隔增大而增大。

4 结论

（1）时间间隔（Δt）的选取对沉降预测的结果影响较大，在采用Asaoka法具体计算时，建议采用相关系数作为直线拟合优劣的主要判断依据，从而选择适合的时间间隔（Δt）。

（2）初始沉降值的取舍对最终沉降量及相关指标有较大影响，建议在计算中将初始沉降值去掉，以达到更好的预测效果。

（3）Asaoka法中关于 Δt的选取（通用方法）有待进一步研究探讨。