扩散波与马斯京根法在栅格汇流演算中的应用比较

姚 成，章玉霞，李致家

(河海大学水文水资源学院，江苏南京 210098)

水文模型作为一种研究流域内复杂水文现象的有效工具，在水文学研究领域中一直发挥着重要作用。就目前的水文模型发展趋势而言，分布式水文模型由于其能够更好地考虑降雨和下垫面条件的空间变异性，能够更好地利用GIS与RS技术等空间信息模拟流域的降雨径流响应，已成为水文模型研究的重要方向［1-2］。现有的分布式水文模型研究多以产流计算的空间变异性为出发点，在模型的构建和应用中更多地追求产流量的高精度模拟，对汇流过程却缺乏足够的重视。汇流过程作为洪水预报的一个重要环节，其模拟精度直接影响模型对流域出口断面流量过程的预报精度，也是流域水文过程模拟的重点与难点。为了使分布式水文模型更好地用于洪水预报，必须加强对汇流过程的重视，需要对分布式水文模型中的汇流过程进行更深一步的研究［3］。

常用的流域汇流演算方法有2种，即基于水量平衡与槽蓄方程的水文学方法和基于圣维南方程组及其简化算法的水力学方法［3-4］。比较而言，水文学方法(如马斯京根法)计算简单，资料需求相对较低，但理论上具有近似性，使用条件会受到限制。而水力学方法可以使汇流演算更具物理性，能够有效处理汇流演算时多方面的影响，但其计算较复杂，对资料的需求也相对较高。笔者以皖南山区呈村流域为例，采用新安江模型进行栅格单元的产流计算，分别采用基于水力学方法的扩散波模型与基于水文学方法的马斯京根法进行栅格单元间的汇流演算，将所构建的栅格型新安江模型［5-7］用于呈村流域的洪水模拟，对2种栅格汇流演算方法进行应用比较，分析在分布式水文模型中采用扩散波与马斯京根法模拟汇流过程的时效性。

1 栅格汇流演算

栅格型新安江模型以流域内每个DEM栅格作为计算单元，并假设在栅格单元内的降雨及下垫面特征空间分布均匀，模型只考虑各个要素在不同栅格之间的变异性。模型以蓄满产流原理为基础，先计算出每个栅格单元的产流量，再采用自由水蓄水库结构将其划分为地表径流、壤中流以及地下径流3种水源，最后根据栅格间的汇流演算次序依次将各种水源演算至流域出口(图1)。对于栅格间的汇流过程模拟，笔者分别采用一维扩散波模型与马斯京根法。

1.1 一维扩散波模型(DW)

扩散波虽然是动力波(圣维南方程组)的一种简化形式，但在许多实际情况下它都适用。而且，利用扩散波模型进行坡面汇流与河道汇流演算都能取得足够高的精度，在很多时候其精度与动力波汇流演算模型的精度相当。本研究在采用扩散波模型进行汇流演算时假设任意栅格单元都是由坡地和河道组成，地下径流与壤中流都直接汇入河道中，因此栅格间的汇流就由坡面汇流及河道汇流组成。

描述坡面水流运动的一维扩散波方程组为

图1 栅格汇流演算示意图Fig.1 Schematic representation of cell-to-cell flow routing

式中:hs——坡面水流的水深，m;us——坡面水流的平均流速，m/s;qs——单位时间内所计算的坡面径流深，m/s;t——时间，s;x——流径长度，m;Soh——沿出流方向的地表坡度;Sfh——沿出流方向的地表摩阻比降。

在进行栅格间汇流演算时，式(1)需要在每个栅格单元上进行离散，其中的连续性方程可表示为

式中:Agc——栅格单元的面积，m2;Qsin——栅格单元的地表径流入流量，m3/s，Qsin=Qsup+Qs;Qsup——上游栅格地表入流流量，m3/s;Qs——当前栅格的地表径流量，m3/s;Qsout——栅格单元的地表径流出流量，m3/s。

本研究采用基于两步(预测步—校正步)MacCormack算法的二阶显式有限差分格式进行式(1)、式(2)的求解［8-10］。该差分格式为显式差分，其稳定性条件为

式中:g——重力加速度，m/s2;Δt——计算时间步长，s;Δx——栅格单元间汇流路径的长度(正向出流时Δx=dc，斜向出流时 Δx =dc)，m;dc——栅格单元边长，m。

描述河道水流运动的一维扩散波方程组为

式中:Ach——河道的过水断面面积，m2;Qch——河道流量，m3/s;ql——单宽旁侧入流，m2/s;hch——河道水深，m;Soc——河道坡度;Sfc——河道摩阻比降。

对于式(4)的求解，同样采用基于MacCormack算法的显式差分格式。

1.2 基于栅格的马斯京根法(MK)

根据栅格间汇流演算次序，依次将地表径流、壤中流、地下径流以及河道水流分别演算至流域出口。以Qs为例(图2)，a，b，c 栅格的流量分别为 Qa，Qb，Qc，出流量Qa'，Qb'，Qc'可以通过马斯京根法计算得到:

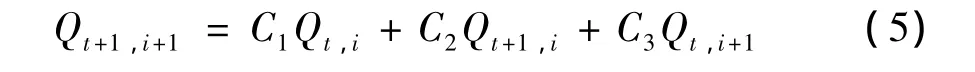
在t时刻，若栅格d的产流量为 Qs，t，则其出流可表示为

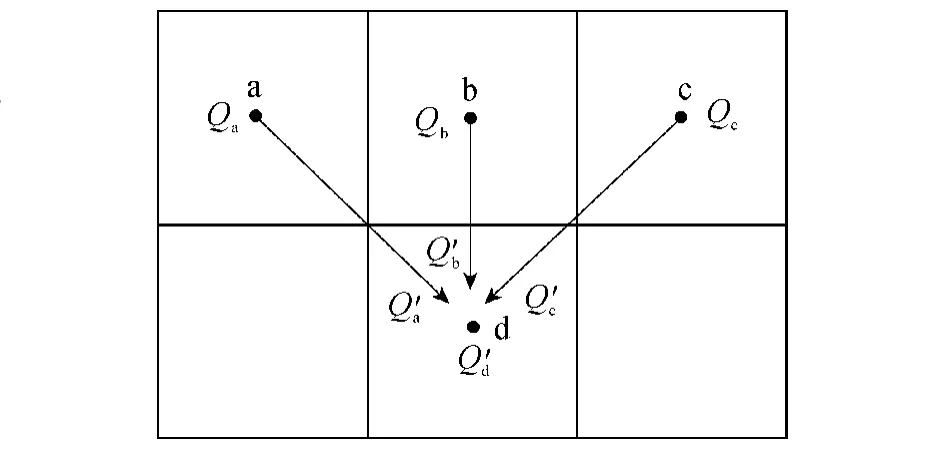
图2 基于栅格的马斯京根法示意图Fig.2 Schematic representation of cell-to-cell Muskingum method

其中

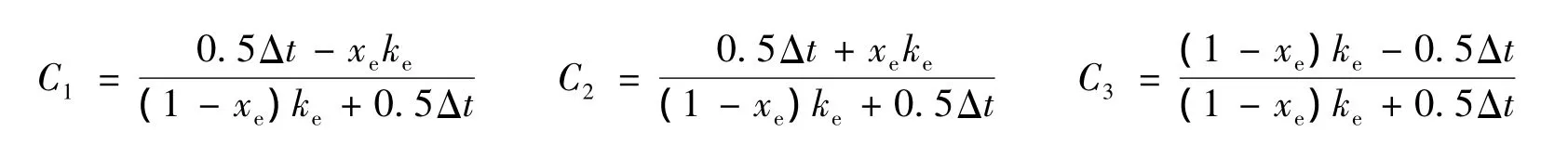
式中:xe——流量比重因子;ke——蓄量常数;fch——地表径流出流量汇入河道的比例。

1.3 栅格间汇流演算次序

栅格汇流演算次序即分布式水文模型在进行汇流演算时所需用到的栅格间演算优先次序。计算步骤如下:(a)对原始DEM矩阵进行预处理，生成研究流域的流向矩阵与累计汇水面积矩阵。(b)初始化栅格演算次序矩阵，将研究流域内的栅格单元全部赋值为零，在累计汇水面积矩阵的基础上，对于矩阵内属于研究流域的且栅格值为1的栅格演算次序赋值n=1(n代表栅格演算次序)。(c)叠加n=n+1，逐个扫描n=0的栅格，假设当前栅格为i，根据流向矩阵判断如下:若流向i的相邻栅格中演算次序均非零，则i的演算次序为n;否则为零。(d)重复步骤c，直至研究流域的出口栅格演算次序已被赋值。

2 参数确定

对于栅格型新安江模型参数的确定，先根据参数的物理意义，利用地貌特征、植被覆盖、土壤类型等下垫面空间信息，结合已有的应用经验对参数取值做出前期估计，然后再根据参数估计的应用结果甄选出敏感参数，最后再利用实测的出口流量过程对敏感参数进行率定和检验［10-11］。

当采用DW方法进行栅格汇流演算时，汇流参数包括Soh，nh(地表曼宁糙率系数)，Soc，nc(河道曼宁糙率系数)以及α(栅格单元的河道宽度指数)。而当采用MK方法时，汇流参数包括xe与ke。由于模型在汇流演算时考虑了河道排水网络的影响，因此2种汇流方法的参数还包括fch。根据已有的研究成果，任意栅格单元的Soh与Soc可以直接通过DEM分析得到，fch也是在流域数字化的基础上利用面积比例法进行计算，α则是通过分析流域内已有的实测断面资料获取［7，11］。nh与nc在扩散波汇流演算中属于敏感参数，nh的确定可以根据栅格单元的植被类型，参考应用经验赋予对应的估值。在此基础上，本文定义了一个空间分布均匀的糙率比例因子μnh，并利用观测资料对该因子进行率定，即任意栅格单元的坡面汇流糙率nh'=μnhnh。nc的计算公式为［12］

式中:Ad——栅格单元的上游汇水面积(可利用累积汇水面积矩阵确定)，km2;n0——计算系数，可以由流域出口点实测的水位-流量关系反算得到，当出口点无实测资料时需要对n0进行率定。

对于xe与ke的确定，暂没有考虑其空间分布不均的问题，而是采用流域内栅格单元统一赋值的方法。xe相对不敏感，按一般经验定值即可。ke属于敏感参数，反映的是不同径流成分在栅格单元的汇流时间，ke越小表明汇流速度越快，则对应洪水过程的峰现时间将有所提前，峰值也会相对增大。由于河道水流、地表径流、壤中流与地下径流在汇流速度上存在差异，因此在率定ke时需对其进行区分。

3 应用实例

3.1 研究流域概况

选择位于皖南山区的呈村流域作为研究流域，该流域邻近东南沿海，四季分明，气候温和，属亚热带季风气候区。呈村流域控制面积为290km2，地势南高北低，相对高差较大，平均海拔高程为583 m，流域河道平均坡度为0.95%，最大汇流路径长度为36 km。流域内植被良好，雨量充沛，多年平均降雨量约为2 100 mm，流域降水在年内、年际分配极不均匀，为典型的湿润流域。该流域植被类型主要包括常绿针叶林、落叶阔叶林、混合林、森林地、林地草原、牧草地与作物地，土壤类型主要为黏壤土。流域内有10个雨量站，具有1986—1999年32场洪水过程的时段资料，其中前22场洪水过程资料用于模型参数率定，其余资料用于模型参数检验。呈村流域水系及其雨量站分布见图3。

3.2 结果分析

在应用模型进行呈村流域的洪水模拟时，栅格单元的分辨率为1 km×1 km(30"×30")，率定的参数主要包括μnh，n0，xe及ke，其余参数则是在已有经验的基础上利用下垫面信息确定。例如，当根据植被类型确定nh时，对于常绿针叶林、落叶阔叶林、混合林及森林地，nh的取值均为0.10，而对于林地草原、牧草地与作物地，nh的取值分别为0.30，0.17 及0.35［11］。参数 μnh，n0，xe的率定结果分别为1.50，0.06，0.30;河道水流、地表径流、壤中流和地下径流对应的ke率定结果分别为0.06，0.10，0.60和1.00。

对于呈村流域率定期内的22场洪水过程而言，DW方法模拟的径流深相对误差(RRE)介于 -12.4% ～15.4%之间，洪峰相对误差(RPE)介于 -19.7% ～29.5%之间，峰现时差(PTE)介于-3～4 h之间，确定性系数(DC)介于0.68～0.99之间;MK方法模拟的RRE，RPE，PTE误差范围分别为-13.4% ～19.7%，-21.6% ～27.8%，-3～6h，DC介于0.80～0.98之间。对于检验期内的10场洪水过程而言，DW 方法模拟的RRE，RPE，PTE误差范围分别为 -12.7% ～9.6%，-18.6% ～16.0%，-10～0 h，DC介于0.93～0.97之间;MK方法模拟的 RRE，RPE，PTE误差范围分别为 -15.0% ～4.2%，-23.4% ～17.7%，0～9 h，DC介于0.92～0.98之间。在计算效率方面，MK方法明显优于采用显示差分格式的DW方法。平均而言，在30"分辨率情况下，MK方法对于呈村流域每次洪水过程(平均约7 d)的计算时间约为1.5 s，而DW方法则需要近22 s。分辨率越高，两者之间的差别越大。表1为采用2种汇流方法模拟呈村流域洪水过程的合格率、平均相对误差水平以及DC均值的统计结果。图4为摘录的2次实测与模拟洪水过程线的比较。应用结果表明，DW和MK方法对于呈村流域洪水过程的模拟精度基本相当，均能达到甲级，采用这2种方法进行栅格间的汇流演算均能够取得较好的应用效果。

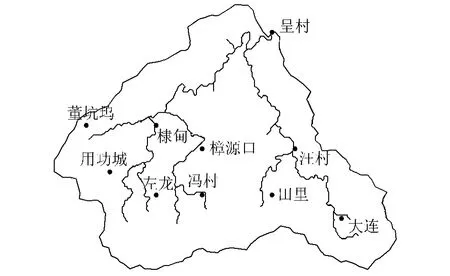
图3 呈村流域水系及雨量站分布Fig.3 Drainage network and locations of gauge stations in Chengcun watershed

表1 采用DW法与MK法的模型模拟结果误差统计Table 1 Accuracy statistics of model simulation results using cell-to-cell diffusion wave and Muskingum routing methods

虽然2种汇流方法在模拟精度上较为相近，但在实际应用时仍然存在一定的差异。DW方法参数的物理意义较明确，参数的空间分布能够通过地貌特征、植被类型等信息获取，能够较好地反映下垫面特征的空间变异性，不仅能输出流域出口断面的水位、流量过程，而且能输出各个计算时段对应的水深、流速等变量的空间分布。且DW方法考虑了水流运动中的压力项，因而对坡度平缓地区的适用性较好。此外，DW方法对于无资料地区的洪水演算也具有一定的适用性。以呈村流域为例，即使令μnh=1，即不利用观测资料对其率定，只根据植被类型确定任意栅格单元的nh值，也能取得一定的应用效果。DW方法的缺陷主要是对于输入信息的需求较高，计算相对复杂，运算效率较低。当采用显示差分格式对扩散波方程进行求解时，为了保证差分格式的稳定，计算时间步长不宜过大，栅格单元分辨率越高则该时间步长越小，需要的模型运算时间也就越长。与DW方法不同的是，MK方法是由水量平衡方程与槽蓄方程推导而来，属于水文学方法，对输入信息的要求相对较低，计算简便，运算效率较高，实用性较好。但该方法对于参数及变量空间分布的描述相对不足，不能充分考虑植被、土壤等下垫面特征对汇流过程的影响，对降雨径流观测资料的依赖性较高，在无资料地区的适用性仍需进一步研究。

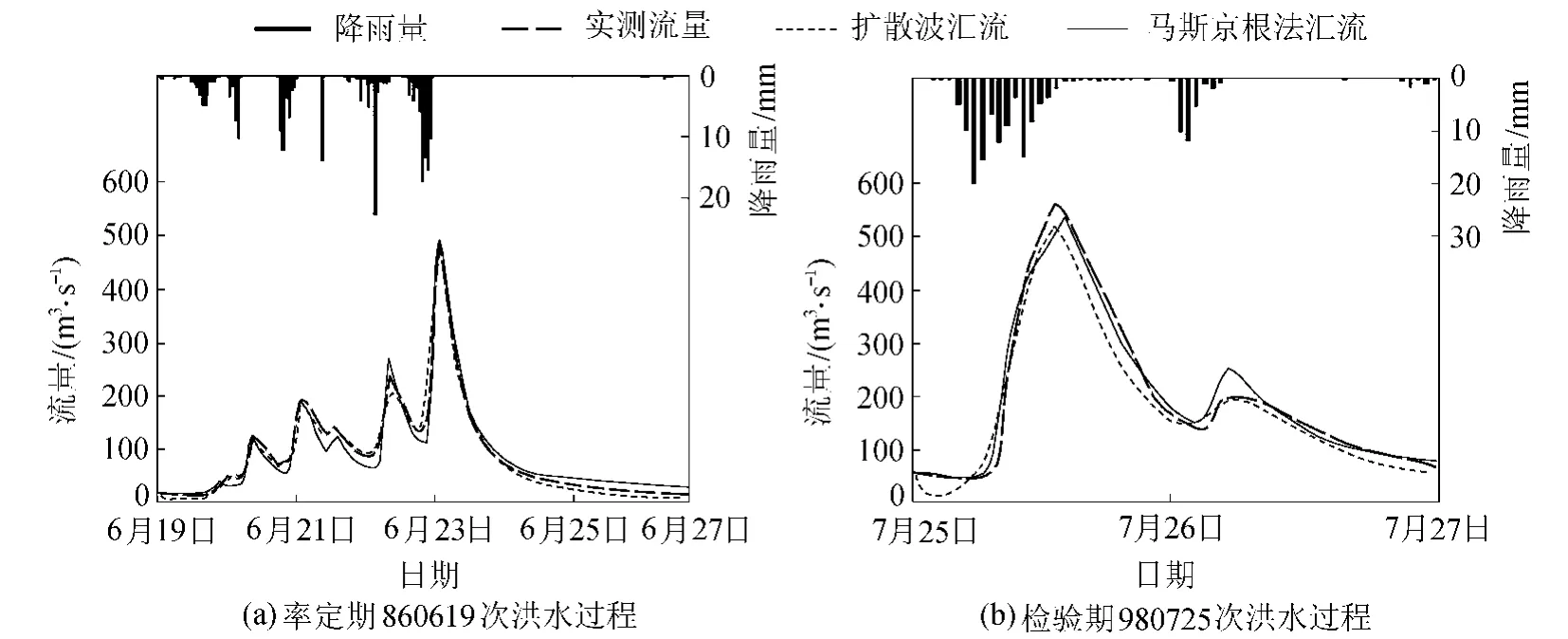
图4 采用DW法与MK方法模拟的洪水过程线比较Comparison of flood hydrographs simulated by cell-to-cell diffusion wave and Muskingum routing methods

4 结 语

考虑到分布式水文模型自身的特点，以及无资料地区洪水预报工作的实际需要，采用何种方法进行计算单元间的汇流演算已成为水文科学研究中的热点与难点问题之一。本文以皖南山区呈村流域为例，针对DW与MK这2种栅格汇流演算方法开展应用比较，结果表明，它们均能较好地用于呈村流域的洪水模拟，能够取得较高的模拟精度。通过对2种方法进行对比分析，发现DW方法有较好的物理基础，能够利用地貌特征、植被覆盖、土壤类型等下垫面信息对参数及其空间分布作出估计，对于无资料地区具有一定的适用性，但其运算效率相对较低，对于大尺度流域的实用性尚需探讨。而MK方法却计算简便，实用性较好，但其对于观测资料有较高的依赖性，不能很好地考虑参数及变量的空间变异性。如何进一步挖掘2种方法的物理内涵，使其更好地用于分布式水文模型，还有待更深入的研究。

［1］芮孝芳，黄国如.分布式水文模型的现状与未来［J］.水利水电科技进展，2004，24(2):55-58.(RUI Xiaofang，HUANG Guoru.The present and future of the distributed hydrological models［J］.Advances in Science and Technology of Water Resources，2004，24(2):55-58.(in Chinese))

［2］熊立华，郭生练.分布式流域水文模型［M］.北京:中国水利水电出版社，2004.

［3］芮孝芳.水文学研究进展［M］.南京:河海大学出版社，2007.

［4］李致家，孔凡哲，王栋，等.现代水文模拟与预报技术［M］.南京:河海大学出版社，2010.

［5］李致家，姚成，汪中华.基于栅格的新安江模型的构建和应用［J］.河海大学学报:自然科学版，2007，35(2):131-134.(LI Zhijia，YAO Cheng，WANG Zhonghua.Development and application of grid-based Xin’anjiang model［J］.Journal of Hohai University:Nature Sciences，2007，35(2):131-134.(in Chinese))

［6］李致家，姚成，章玉霞，等.栅格型新安江模型的研究［J］.水力发电学报，2009，28(2):25-33.(LI Zhijia，YAO Cheng，ZHANG Yuxia，et al.Study on gird-based Xin’anjiang model［J］.Journal of Hydroelectric Engineering，2009，28(2):25-33.(in Chinese))

［7］YAOCheng，LI Zhijia，BAOHongjun，et al.Application of a developed Grid-Xin’anjiang model to Chinese watersheds for flood forecasting purpose［J］.Journal of Hydrologic Engineering，2009，14(9):923-934.

［8］WANG M，HJELMFELT A.DEM based overland flow routing model［J］.Journal of Hydrologic Engineering，1998，3(1):1-8.

［9］JAIN M，SINGH V.DEM-based modelling of surface runoff using diffusion wave equation［J］.Journal of Hydrology，2005，302:107-126.

［10］YAO Cheng，LI Zhijia，YU Zhongbo，et al.A priori parameter estimates for a distributed，grid-based Xin’anjiang model using geographically based information［J］.Journal of Hydrology，2012，468/469:47-62.

［11］姚成，纪益秋，李致家，等.栅格型新安江模型的参数估计及应用［J］.河海大学学报:自然科学版，2012，40(1):42-47.(YAO Cheng，JI Yiqiu，LI Zhijia，et al.Parameter estimation and application of grid-based Xin’anjiang model［J］.Journal of Hohai University:Natural Sciences，2012，40(1):42-47.(in Chinese))

［12］KOREN V，REED S，SMITH M，et al.Hydrology laboratory research modeling system(HL-RMS)of the national weather service［J］.Journal of Hydrology，2004，291:297-318.