受轴向压力开孔板极限强度有限元分析研究

刘慧泉，张世联，褚 洪

(上海交通大学船舶海洋与建筑工程学院，上海 200240)

大多数钢结构工程都使用板来提供必要的强度，例如海洋平台的甲板、纵桁的腹板等，这些板要承受较大的面内压力。出于减轻重量、人员通行、辅设装置等原因，不可避免的要在板上开孔。开孔会在一定程度内减小板的承载能力，研究开孔板的极限强度在工程中具有较大的实际意义。

受轴向面内压力的板在一定的载荷下会失稳而发生屈曲，而与杆件不同的是，板在失稳后并不是立刻被破坏而完全失去所有刚度。在平台结构中，某一块板在失稳后，四周受到其他构件的支撑，无法向杆件那样自由趋近而导致破坏。实际上，板在失稳后由于中面被拉长还产生了薄膜应力来抵抗变形。因此板在失稳后内部应力将重新分配，仍然可以继续承受载荷直到板中部分截面应力全部达到屈服值为止，这时板的强度称为极限强度［1］。

板的极限强度涉及到多种非线性问题，如板的中面力、板的大挠度，以及材料的塑性变形等。这些问题比较复杂，运用传统的理论计算求解遇到很大的困难。近年来有限元数值计算的发展为此类非线性问题的解决带来了长足的进步。Harada对受轴向开孔矩形板的极限强度在数值计算的基础上提出了塑性修正公式［2］;Paik给出了受到双轴向压力及剪力的开孔矩形板的极限强度经验公式［3］;Shanmugam等提出了受轴向压力的方形开孔板极限强度的经验公式［4］;Maiorana等分析了受到局部载荷的开孔板的极限强度［5］;Cheng等分析了开孔方板的极限强度并对补强效率进行了对比［6］。

以上对开孔板的极限强度研究多集中在四周自由支持的开圆孔矩形板上，而对其他类型的边界条件和开孔形状考虑较少。在海洋平台结构中，许多主要构件并非四周都受到支持，且许多开孔形状也不是规则的圆形。使用ABAQUS/Standard求解器的弹塑性大挠度分析功能，在三种边界条件下，对不同边长比的开圆孔板及开有不同类型孔的板的极限强度进行了计算和分析，最后提出了预报极限强度简单实用的经验公式。

1 有限元模型

1.1 边长比分析

模型为中心开有圆孔的矩形板，板宽 b=0.4 m，边长比分别为 1∶2、1∶4、1∶6、1∶8，厚度与板宽比 t/b取0.02、0.025、0.03、0.035，对应无量纲的柔度系数 β 分别为 1.936、1.549、1.291、1.107。板的边界条件有三种:BC1为四周自由支持;BC2为三边固定支持、一长边自由;BC3为三边自由支持，一长边自由。在实际的平台构件中，甲板板可以使用四边自由支持的边界，而纵桁、横梁的腹板的边界条件应当介于三边固定支持和三边自由支持之间。板沿长边方向受到面内压载荷。模型边界及载荷示意如图1所示，图中边界条件s表示自由支持，c表示固定支持，空白为完全自由。

1.2 孔形状分析

开孔在板的中心，共有三种类型:圆孔、腰圆孔和方形孔。其中腰圆孔取工程中常用的形式，两端为半圆，中部为正方形。为了合理的比较各类孔对板的极限强度的影响，三种孔的高度h与板宽b的比值h/b取为0.3、0.4、0.5、0.6、0.7。板的边长比取为1∶4，边界条件和厚度取值同上。模型的网格划分如图2所示。

图1 模型载荷及三种边界条件Fig.1 Load and three boundary conditions of model

图2 模型有限元网络Fig.2 Finite element mesh

2 计算结果分析

2.1 边长比影响

由图3可以看出，在相同的柔度系数β下，极限强度最大的为BC1，其次为BC2，最小的是BC3。一般情况下，破坏应当发生在开孔附近，受到的边界约束越多，约束越强，产生中面力的范围越大，就可以更有效的抵抗变形，从图4的应力分布云图中能够准确地看出这点。图4分别是三种边界条件下板达到极限状态时的Von Mises应力云图。图4(a)中模型的边界是BC1，很明显在四周都有支持的情况下，板在发生破坏时圆孔边缘到上下边界的两块“板条”同时达到了屈服应力。而对于BC2来说，参考图4(b)，板的下部没有约束，靠近下边界的板可以自由变形，不能产生中面力来承担继续施加的载荷，能获得支撑的只有上部的“板条”，板内可以有效承受的载荷的面积比BC1小，当其达到屈服应力时就发生了破坏，因此极限强度也较小。BC3的极限强度比前两者小得多，因为上边是自由支持，下边没有约束，极易形成半波失稳，且在无约束的情况下靠近孔下边缘部分的板发生大挠度变形，应力迅速增大造成破坏，从图4(c)可以清楚地看到只有很窄的一部分板达到屈服应力。

图3 边长比1∶4开圆孔板极限强度Fig.3 The ultimate strength of perforated plates with circular holes with side ratio 1∶4

图4 开孔板在极限状态时的Von Mises应力分布Fig.4 Von-Mises stress distribution of perforated plates under ultimate condition

开孔板的极限强度很大程度上取决于长边的约束条件，而承担较大应力且发生破坏的部分总集中在孔边缘附近到边界的“板条”上，远离孔之后的应力水平都不大，所以无论是增加还是减小板的长度对于有效承担载荷的“板条”影响都很小，极限强度也不发生很大的改变。图5给出了不同边长比的板的极限强度对比，任一边界条件下，边长比对于开孔板的极限强度的影响很小，可以忽略。因此在计算不同开孔形式的板的极限强度时没有必要选取多种边长比，下文仅对1∶4的板进行分析。

2.2 开孔类型影响

三种类型的开孔对板的极限强度影响如图6所示，由于篇幅原因，这里只列出了t=10 mm(β=1.549)的计算结果。在BC1和BC2的边界条件下，三种开孔形式的区别较小，这是因为在较强的边界约束下，应力较大且首先发生破坏的部分只与最小截面处的截面面积有关，与孔的形状关系不大。但是可以发现开圆孔的板的极限强度略大于开腰圆孔和方孔的板。这是因为圆孔中心位置处的“板条”向两边逐渐变宽，相对于宽度一直不变的腰圆孔和方孔，能承受最大载荷的有效板面积略大，因此可以获得较高的极限强度。

图5 不同边长比开孔板极限强度Fig.5 The ultimate strength of perforated plates with different side ratio

而BC3的情况却大不相同，开腰圆孔板的极限强度随着开孔尺寸的增大急剧减小，比开圆孔和方孔的板要小30%左右。这是因为三边自由支持、一边自由的板受到轴向压力时，靠近自由边的部分可以不受阻碍的趋近，容易形成半波，类似于杆件的失稳。一旦有半波形成，在挠度最大的板中下部将会产生非常大的应力，破坏也随之发生。因此BC3边界板的极限强度取决于板的自身刚度，腰圆孔的面积大约是圆孔和方孔的两倍，又处于变形最大的中部区域，导致板的刚度损失较大，故其极限强度要大大小于开圆孔和方孔的板。

图6 t=10 mm三种开孔板极限强度Fig.6 The ultimate strength of three kinds of perforated plates with thickness t=10 mm

经过以上分析以及对大量计算数据的处理归纳，给出两个经验公式来对开孔板的极限强度做出初步预报。对于四边自由支持的开孔板，可以认为在板较厚时(β＜1.5)，开孔处截面面积最小的“板条”达到屈服就发生破坏，但是孔较小的板要作相应修正，极限强度用下式表示:

Paik等根据大量计算得到的四边自由支持的开圆孔板在柔度为1.5时极限强度的经验公式为:

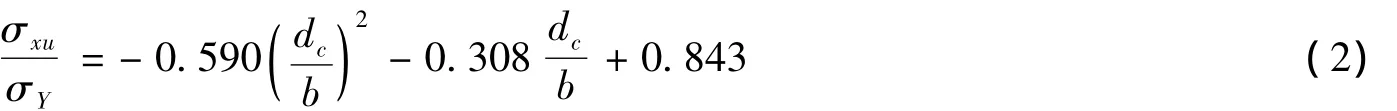
式中:dc为圆孔直径。不难看出，式(1)与式(2)展开后有同样的形式，只是系数略有不同。

对于三边固定支持，一边自由的开孔板，可以认为在板较厚时(β＜1.5)，位于孔上边缘与有约束的边界之间的板达到屈服时就发生破坏，但是由于固定约束的存在，板的其他部分也可以有效承担部分载荷，如图4(b)中下部的部分板在极限状态时也达到了屈服值。因此板的极限强度要高于只考虑上部分板屈服的情况，极限强度值要作适当修正:

式中:α为形状系数，圆孔取1，方孔和腰圆孔取1.15。

图7和图8给出了部分有限元计算结果与以上经验公式得到的极限强度数值的对比，可以看出，式(1)、(3)能够较好的吻合有限元计算结果，其中式(1)在计算开圆孔板时结果偏小，精度低于Paik所得的公式，但对开腰圆孔板，特别是孔较大时，有相当的精度。当β＜1.5时，开孔板极限强度随β减小(及厚度增加)而略有增加，由公式得到的极限强度数值小于有限元结果，偏向于保守和安全。式(1)与式(3)对于在初步设计时估算开孔板的极限强度有一定的实用性。

图7 BC1有限元计算结果与经验公式值对比Fig.7 Comparison of results between FEM and empirical formulae under BC1

图8 BC2有限元计算结果与经验公式值对比Fig.8 Comparison of results between FEM and empirical formulae under BC2

3 结语

对三种边界条件下，不同边长比及开三种类型孔的板的极限强度进行了计算和分析，得到以下几点结论:

1)边长比对三种边界条件下的开孔板的极限强度影响很小，可以忽略不计，在实际分析板的极限强度时只需取出包括开孔部分适当长度的板。

2)边界条件对开孔板的极限强度影响很大，约束越强，板的极限强度越大。针对三种边界条件进行计算，四边自由支持的情况极限强度最大，三边固定支持、一边自由的情况略小，三边自由支持、一边自由的情况最小。

3)在四边自由支持和三边固定支持的边界条件下，三种开孔形式的板的极限强度较为相近，而三边自由支持的边界条件下，开腰圆孔板的极限强度比开圆孔和方孔的板要小很多。

4)通过计算归纳，给出了一定范围内的开圆孔和腰圆孔的板在四边自由支持和三边固定支持边界条件下的极限强度经验公式，与现有经验公式和有限元计算结果进行了对比，该公式吻合性较好且偏于保守。

［1］ Owen F Hughes.Ship Structural Design［M］.Society of Naval Architects＆;Pap/Cdr edition，2005.

［2］ Minoru Harada，Masahiko Fujikubo.Estimation of buckling and ultimate strength of rectangular plate with cutout［C］∥International Offshore and Polar Engineering Conference.2002.

［3］ Paik J K，Gumjeong-Gu.Ultimate strength of steel plates with a single circular hole under axial compressive loading along short edges［J］.Ships and Offshore Structures，2007，2(4):355-360.

［4］ Shanmugam N E，Thevendran V，Tan T H.Design formula for axially compressed perforated plates［J］.Thin-Walled Structures，1999，34:1-20.

［5］ Emanuele Maiorana，Carlo Pellegrino，Claudio Modena.Non-linear analysis of perforated steel plates subjected to localized symmetrical load［J］.Journal of Constructional Steel Research，2009，65:959-964.

［6］ Cheng Bin，Zhao Jincheng.Strengthening of perforated plates under uniaxial compression:buckling analysis［J］.Thin-Walled Structures，2010，48:905-914.