张力腿平台关键部位疲劳可靠性分析

崔 磊，何 勇，徐伽南，金伟良

(浙江大学结构工程研究所，浙江杭州 310058)

张力腿(TLP)平台由于具有运动性能好、抗环境荷载作用能力强等优点，已成为深海油气资源勘探、开发、生产和加工处理的一种主要平台。然而，由于深海环境恶劣，其结构在风、浪、流等环境载荷以及作业动态载荷作用下容易发生疲劳，严重威胁了平台的安全可靠运行。因此，对于高成本高风险的深海油气资源的勘探和开发而言，深入开展TLP平台结构疲劳可靠性的研究具有重要意义。

目前，用于海洋结构疲劳可靠性分析的方法主要有两种，即S-N曲线法和断裂力学方法。国内外许多学者已经应用这两种方法开展了海洋平台疲劳可靠性的研究工作。Kjerentroen和Wirsching［1］研究了TLP平台的张力腿，假设其为一个串联结构体系，分析了张力腿的疲劳可靠性。Hove，Hovde和Moan［2-3］研究了TLP平台系索系统疲劳可靠性，提出了一种高效的系索疲劳可靠性计算方法，拓展了Ximenes［4］系统模型。Siddiqui和Ahmad［5-6］应用S-N曲线法和断裂力学方法研究了随机风浪荷载作用下TLP平台系索的疲劳断裂可靠性，应用一阶可靠度方法和蒙特卡罗方法分析了各种随机变量对TLP平台系索可靠性的影响及参数敏感性［7］。张剑波［8］针对半潜式钻井船典型节点的疲劳寿命进行了计算，并对几个危险节点进行了可靠性分析和裂纹扩展寿命计算。马网扣等［9］应用疲劳谱分析方法对深水半潜式钻井平台节点进行了研究，总结出了半潜式平台疲劳寿命谱分析流程。基于Miner线性损伤累积理论和随机响应首次超越破坏原则，邓鹏等［10］分析了半潜式平台关键点的疲劳可靠性。对于TLP平台，已有的研究主要集中在TLP平台张力腿系索系统的疲劳分析，而针对TLP平台在深海复杂环境作业时特殊结构构造和连接的疲劳问题，国内外在这方面的研究成果不多。

应用S-N曲线法和断裂力学方法较为系统地研究了TLP平台关键部位的疲劳可靠性。通过平台结构分析，建立了TLP平台整体模型和关键部位的中间局部模型和精细子模型，结合中国南海海况，进行了不同工况下平台的应力响应分析。以TLP平台整体模型和中间局部模型的计算结果为边界条件，应用子模型技术，采用外插法计算了关键部位关键节点的热点应力，对比分析了平台关键部位的疲劳可靠性。

1 TLP平台模型与海况荷载分析

1.1 结构有限元模型

TLP平台浮体结构由浮箱、立柱、上部甲板及设备三部分组成，其示意图和设计参数如图1和表1所示。选用通用有限元软件ANSYS进行分析，所用的单元类型有两类(弹性和弹塑性)共9种。弹性:BEAM4、BEAM44、SHELL63、 PIPE16、 MASS21、COMBIN14， 弹 塑 性: BEAM188、SHELL181、PIPE20， BEAM4、BEAM44、BEAM188为梁单元，SHELL63和SHELL181为壳单元，PIPE16和PIPE20为管单元，MASS21为质量单元，COMBIN14为弹簧单元。壳单元用来定义平台的外部和内部的板壳结构，梁单元用来定义板壳的加筋肋，管单元用来定义平台柱子和上部甲板的连接部位的管，COMBIN14单元用来定义平台的边界条件，TLP平台整体有限元模型如图2所示。

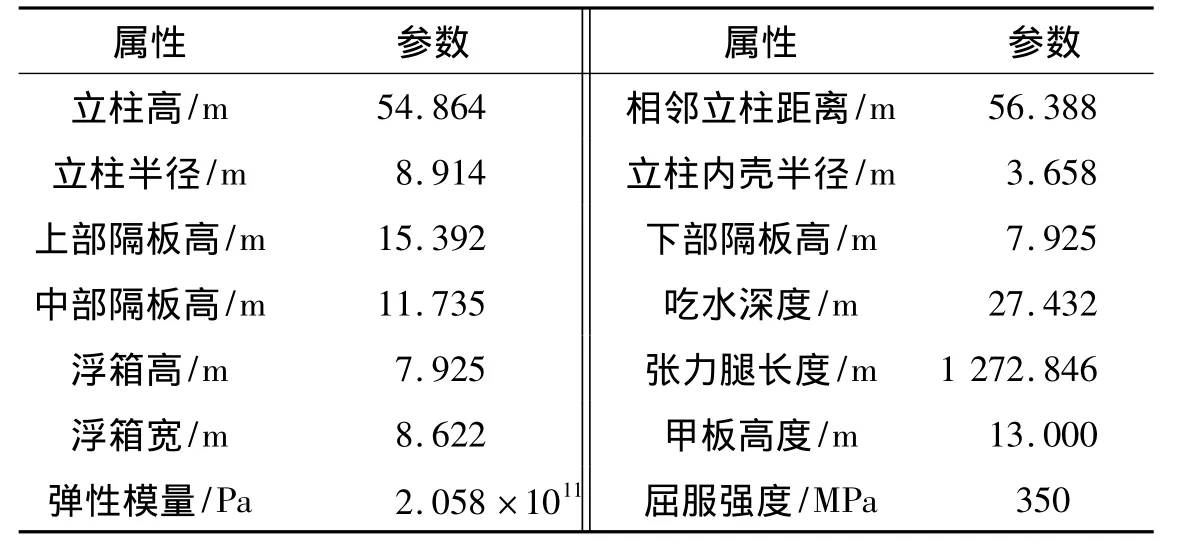
表1 TLP平台主要设计参数Tab.1 Description of TLP

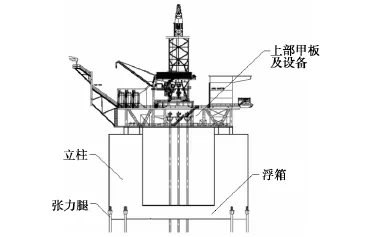
图1 TLP平台浮体结构示意Fig.1 Schematic diagram of floating structure of TLP

图2 TLP平台整体模型Fig.2 Global model of TLP

1.2 海况分析与荷载计算

在任一短期海况中，波浪作为一个均值为零的平稳正态随机过程，其统计特性可用功率谱密度来完全地确定。在疲劳分析中，采用Pierson和Moskowitz给出的适用于无限风区充分发展的波浪谱:

式中:S(ω)为波浪谱密度;ω为波浪圆频率;HS为有义波高;Tz为平均跨零周期。

对于在特定海域作业的海洋平台，其服役期间所遭遇海况的长期分布可由该海区的波浪散布图确定，选择中国南海某海域的波浪散布图如表2所示，确定对疲劳起主要作用的海况。

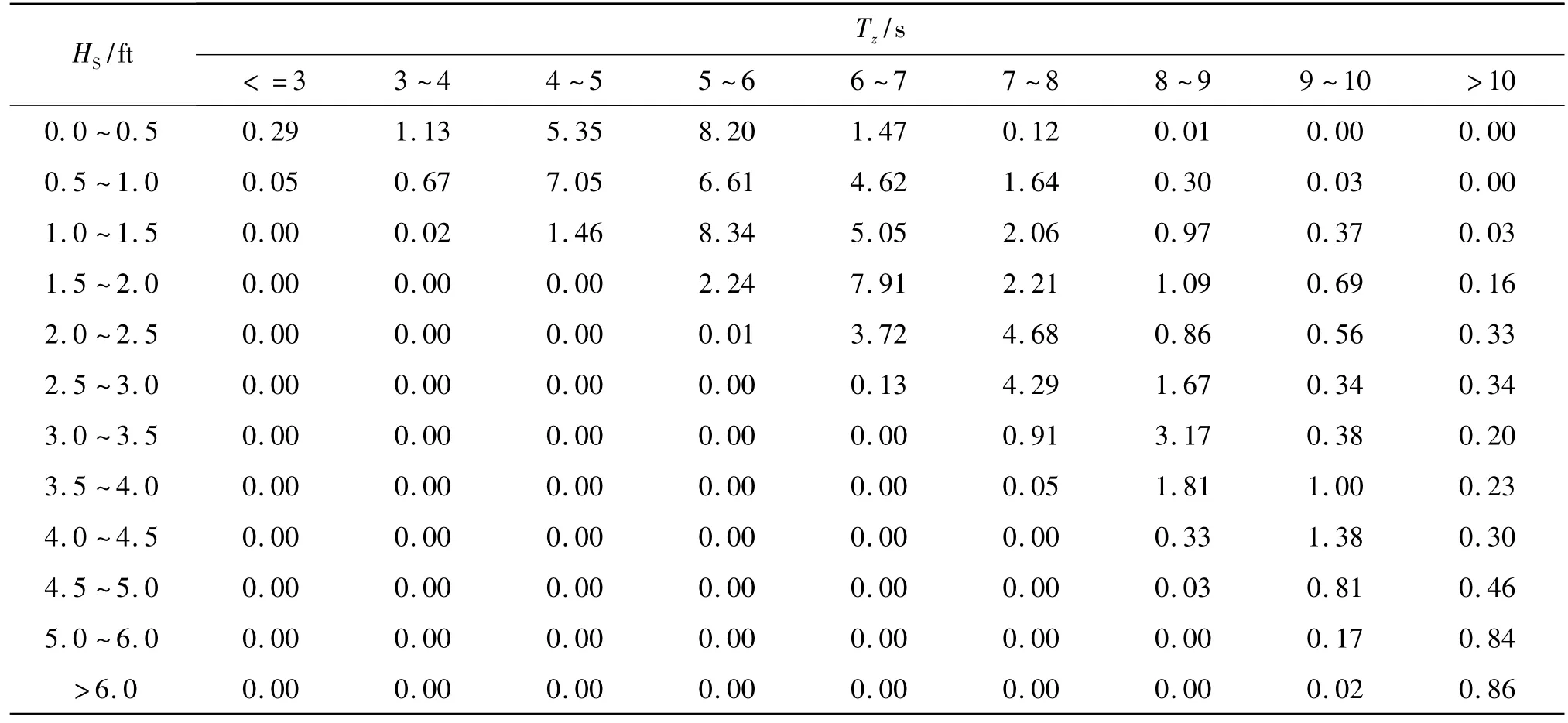
表2 中国南海某海域波浪散布图(ΣP=100)Tab.2 Wave scatter diagram of South China Sea(ΣP=100)

TLP平台在深海作业时承受风、浪、流等环境载荷以及作业动态载荷的作用，文中考虑平台浮体结构的五种荷载作用，分别为结构重力、甲板活荷载、静水压力、波浪荷载和环境风荷载，风浪荷载是TLP平台疲劳分析的主要荷载。结构重力通过施加重力加速度确定，甲板活荷载通过施加质量单元确定，静水压力以水深线性变化的压力形式作用到水面以下立柱及浮箱的外壳上，如图3所示;环境风荷载由受风面大小确定，将风荷载分摊到各构件上;采用水动力软件WAMIT计算平台疲劳分析的波浪荷载，水动力模型如图4所示。通过转换接口把水动力分析结果转化到ANSYS模型，图5给出了TLP平台波浪荷载转化示意图。分析时分别选取入射方向为0°、45°、90°、180°，周期为4～40 s的波浪，计算得到的水动力荷载包括一阶波浪压力及整个平台的惯性力。

图3 TLP平台静水压力示意Fig.3 Schematic diagram of hydrostatic pressure of TLP

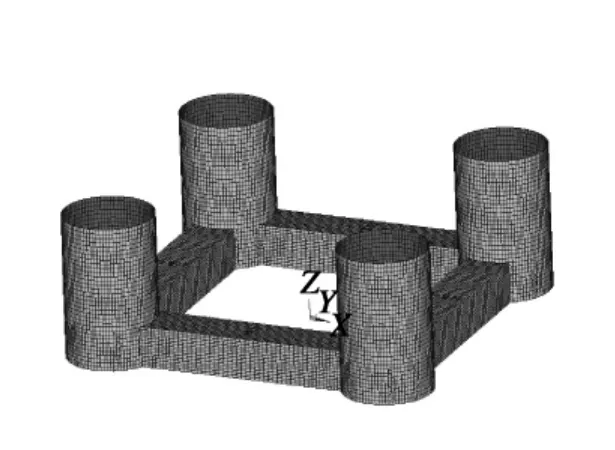
图4 TLP平台水动力模型Fig.4 Hydrodynamic model of TLP

图5 TLP平台水动力荷载示意Fig.5 Schematic diagram of wave loads transformation

2 疲劳可靠性分析方法与随机变量的计算选取

2.1 S-N曲线法和随机变量的计算选取

基于Miner线性累积损伤理论与S-N曲线，结构的疲劳寿命Tf为［5-6］:

式中:A，m为S-N曲线参数;B为疲劳荷载计算过程中不确定因素的随机变量;Δ为结构疲劳损伤度;A，B，Δ均为随机变量;Ω为应力参数。

计算所得的疲劳寿命Tf小于设计寿命TD的疲劳失效概率，用Pf表示:

若各随机变量为对数正态分布，则计算可靠度的极限状态方程可表示:

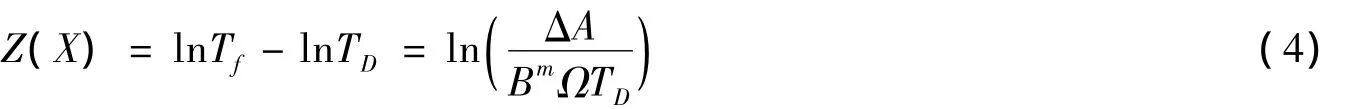
式中:X为基本随机变量。结构的疲劳可靠性指标为:

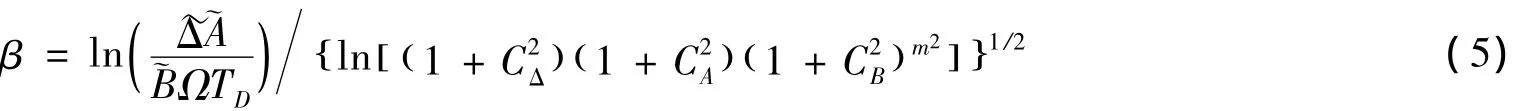
应用S-N曲线法进行平台结构的疲劳可靠性分析时，涉及相关海域波浪散布图数据统计的不确定性、PM谱模拟波浪环境的不确定性、有限元计算模型结构响应的不确定性、波浪荷载计算的不确定性等，因此，随机变量的确定至关重要，关系到分析结果的准确性和合理性。

在 Torng，Kung 和 Wirsching［11-12］，Jiao 和 Moan［13］，Siddiqui和 Ahmad［5-6］等研究的基础上，结合结构材料特性和S-N曲线的相关数据，按照ABS［14］推荐的有阴极保护的S-N曲线，选取B曲线中的m，A及其变异系数，疲劳损伤度Δ根据Wirsching等的研究选择Δ的中值和变异系数，选取参数B的中值与变异系数，表3给出了应用S-N曲线法进行疲劳可靠性分析的各参数取值。

表3 疲劳可靠性分析参数(S-N曲线法)Tab.3 Data of fatigue reliability analysis(S-N curve approach)

2.2 断裂力学方法和随机变量的计算选取

疲劳裂纹扩展分析是基于Paris-Erdogan公式［15］:

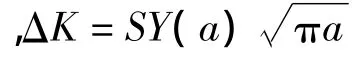
表面裂纹贯穿板厚发生疲劳破坏时，结构的疲劳寿命为［16］:

式中:N为结构的疲劳循环次数;a0为初始裂纹尺寸;ac为临界裂纹尺寸。

考虑应力计算和几何修正系数计算中的不确定性，不同工况下结构的疲劳寿命为:

式中:B为应力幅值计算中不确定的随机变量;BY为几何修正系数Y(a)计算中不确定的随机变量;Ω为应力参数。

若结构的设计寿命为TD，计算结构疲劳可靠度的极限状态方程可表示为:

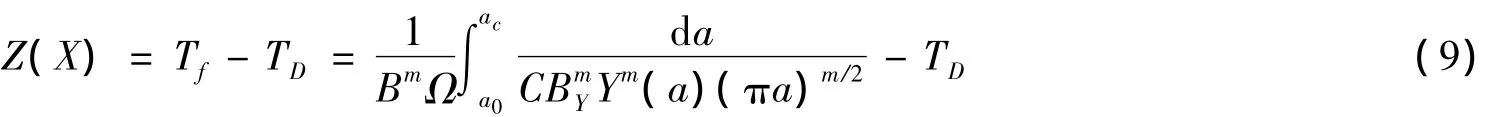
采用一次二阶矩方法，通过迭代计算得到结构的疲劳可靠性指标和失效概率。

应用断裂力学方法进行平台结构的疲劳可靠性分析时，涉及应力强度因子范围计算中的不确定性、材料裂纹扩展性能的不确定性、裂纹初始状态的不确定性、有限元计算模型结构响应的不确定性等。初始裂纹深度a0按照 DNV［17-18］和 ABS［16］确定，临界裂纹尺寸 ac按贯穿板厚选取。材料裂纹扩展参数 m、C参照ABS［16］确定。按照胡毓仁［19］分析 Guedes Soares［20］和 Moan［21］等人的研究给出的形状参数 ξ和应力循环总次数NL的取值方法，确定半潜式平台进行疲劳可靠性分析的ξ和NL。几何修正系数Y(a)及其计算中不确定的随机变量BY参照Newman-Raju［22］公式和BS7910［23］进行计算，表4给出了应用断裂力学方法进行疲劳可靠性分析的各参数取值。

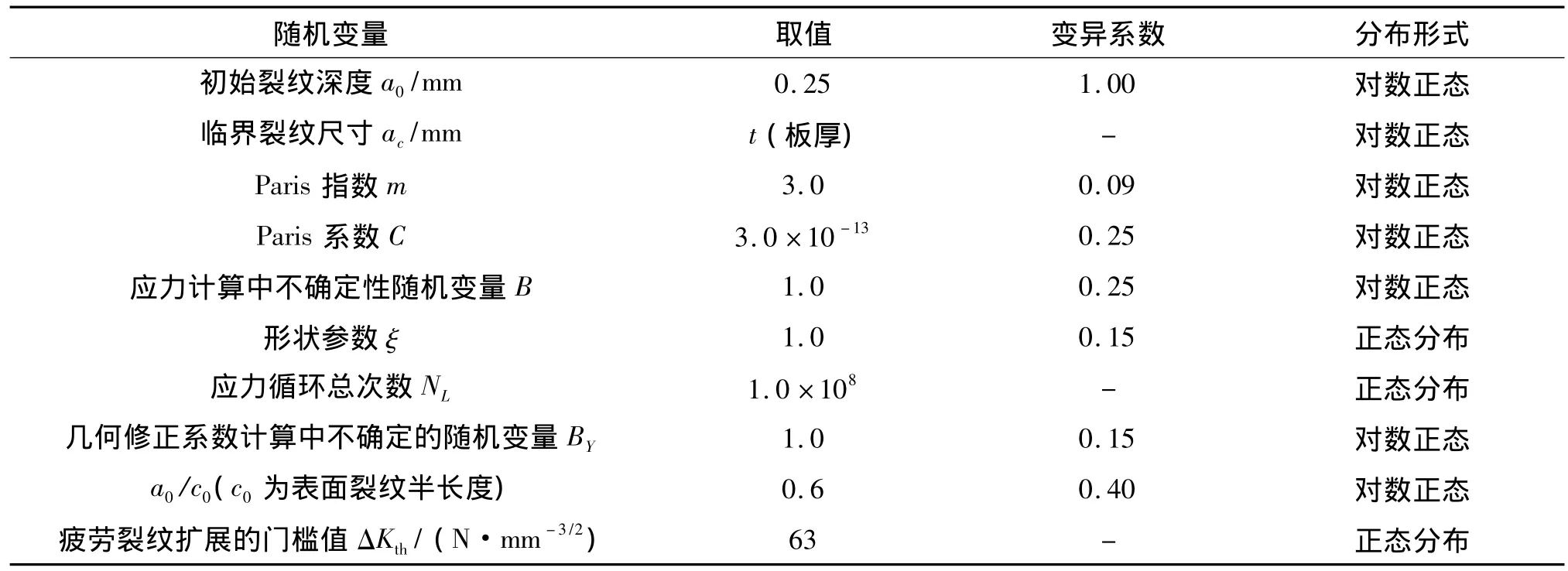
表4 疲劳可靠性分析参数(断裂力学方法)Tab.4 Data of fatigue reliability analysis(F-M approach)

3 关键部位的确定与应力响应分析

不同工况下波浪荷载对平台的作用力有很大的差异，需要分析平台在不同周期、不同浪向下的应力响应，从而确定平台的疲劳关键部位。平台不同工况下的立柱最大垂向弯矩、浮箱最大横向撕裂力、张力腿最大横向扭矩的等效应力分布图如图6所示。从图中可以看出，应力响应较大的部位出现在甲板和立柱连接部位、立柱和浮箱连接部位，这些部位是疲劳可靠性分析的关键部位，如图7所示。

女人在找到他的时候就跟他讲明白了要他调查的内容，在两个月内查清楚一个叫田连民的人，是个国家税务干部，供职于城关税务分局的缉查科，就是这个人把杨剑送进了监狱。

图6 TLP平台整体极限强度等效应力云图Fig.6 Equivalent stress distribution of ultimate strength of TLP

由于平台的整体模型巨大，所以网格划分较粗，单元尺寸较大，且不考虑结构局部的一些细节构造，因此，整体计算结果只能反应出平台受力变化的大致情况。为了得到较为精确的计算结果，需要对平台结构进一步分析，由于TLP平台为对称结构，分析时平台上部和下部各选择了一个关键部位进行研究，即上部的甲板和立柱连接部位、下部的立柱和浮箱连接部位。分别建立了甲板和立柱连接部位、立柱和浮箱连接部位的中间局部模型，如图8和图9所示。

图7 TLP平台关键部位示意Fig.7 Schematic diagram of key parts in TLP

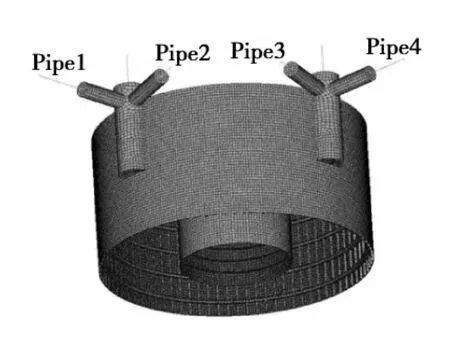
图8 立柱与甲板连接的中间局部模型Fig.8 Middle local model of the joint in deck and column

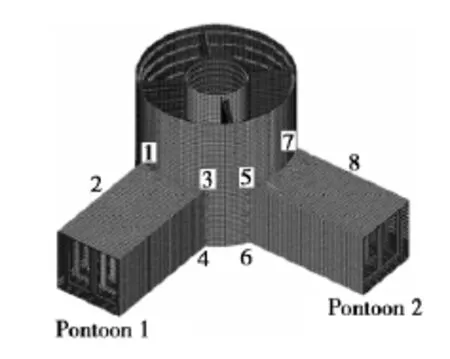
图9 立柱与浮箱连接的中间局部模型Fig.9 Middle local model of the joint in column and pontoon

图8中有四根支杆(Pipe1，Pipe2，Pipe3，Pipe4)与弦杆连接，弦杆与支杆的连接处按逆时针从上部开始每隔90°依次选取四个计算热点(1，2，3，4)，建立精细子模型，如图10所示，其结构构造与真实结构相同。图9中立柱与浮箱连接处上下角点几何突起处的节点在不同工况下应力响应较大，因此选作关键部位的关键节点，角点1、3、5、7为立柱与浮箱 (Pontoon1，Pontoon2)连接的上部角点，角点2、4、6、8为立柱与浮箱连接的下部角点，精细子模型如图11和图12所示，并对关键节点区域的单元进行细化，单元大小与板厚相同。

图10 立柱与甲板连接点的精细子模型Fig.10 Fine refined model in the joint of column and deck

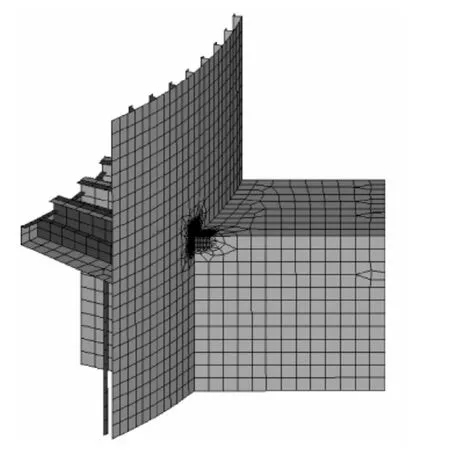
图11 立柱与浮箱连接上部精细子模型Fig.11 Fine refined model in the joint of column and pontoon

图12 立柱与浮箱连接下部精细子模型Fig.12 Fine refined model in the joint of column and pontoon

关键部位精细子模型的应力响应分析采用改进子模型技术，以不同工况下整体模型的计算结果作为中间局部模型切割边界上的边界条件，进行多边界插值，如图13所示;将整体模型中的相应荷载加到局部模型上，进行不同工况下的应力响应分析。然后再以不同工况下中间局部模型的计算结果作为精细子模型切割边界上的边界条件，将整体模型在精细子模型位置的荷载加到精细子模型上，再进行不同工况下的精细子模型应力响应分析。图14给出了其中一种工况下立柱与浮箱连接上部角点的精细子模型等效应力云图。

4 疲劳应力参数计算

根据不同工况下精细子模型的应力响应分析结果，计算各关键节点的热点应力幅值，按照规范ABS［16］中推荐的热点几何应力外插法，如图15所示。P点为焊趾位置，P3t/2、Pt/2为所取外插点的位置，紧靠焊趾沿面板和腹板的交线依次选取四个相邻单元，单元表面最大主应力点P1、P2、P3、P4到焊趾的距离分别为X1、X2、X3、X4，通过Lagrange插值，以其距焊趾的距离为参数得到距节点t/2和3t/2处的应力幅值，再通过线性插值得到焊趾处节点的热点应力幅值Shot为:

图13 中间局部模型边界插值Fig.13 Cut-boundary interpolation of middle local model

图14 立柱与浮箱连接上部角点精细子模型等效应力云图Fig.14 Equivalent stress distribution of fine refined model in upper joint of column and pontoon

图15 几何应力外插法计算热点应力示意Fig.15 Extrapolation of geometric stress to calculate the hot spot stress

基于S-N曲线法和Miner法则，应力参数与应力范围的概率分布及作用频率有关。由不同工况下各个节点的热点应力幅值，可以得出不同周期、不同浪向下的应力传递函数，以立柱与浮箱连接部位的角点为例，图16为立柱与浮箱连接部位各角点浪向0°、90°入射各热点的第一主应力传递函数曲线。

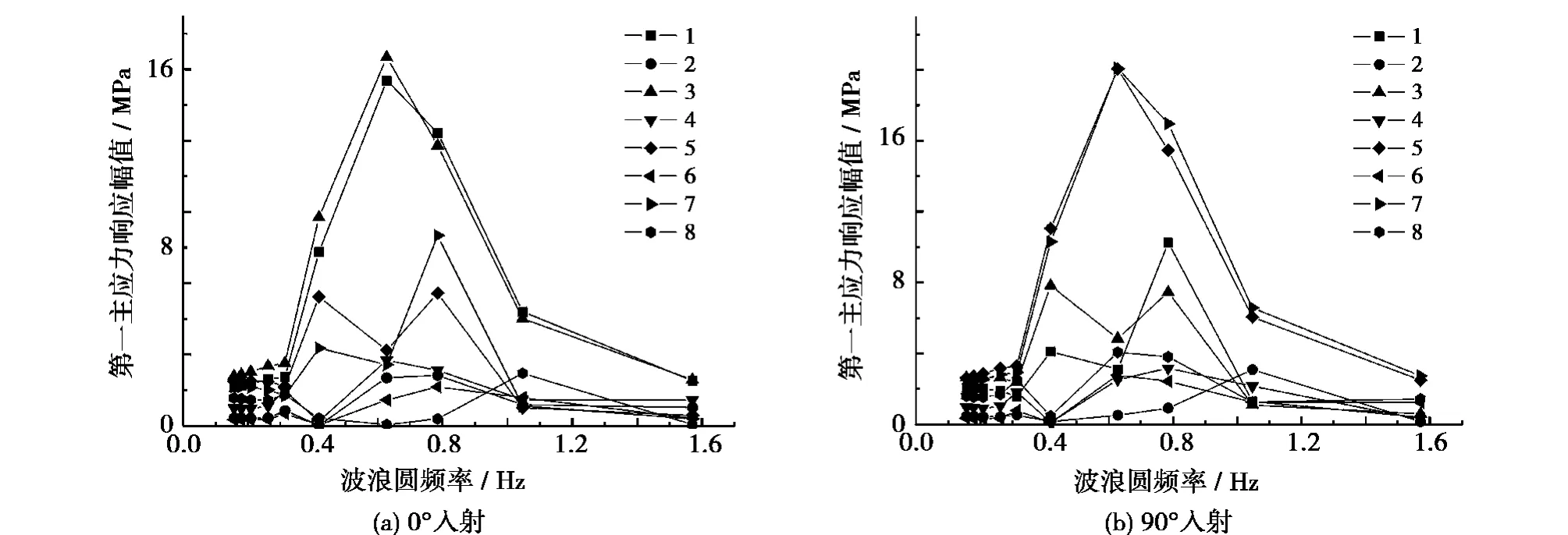
图16 立柱与浮箱上部角点第一主应力传递函数Fig.16 The first principal stress transfer function of upper joint in column and pontoon with wave direction

由疲劳应力传递函数，确定疲劳应力能量谱，计算出谱矩，考虑雨流修正，平台结构的疲劳应力参数用下式计算:

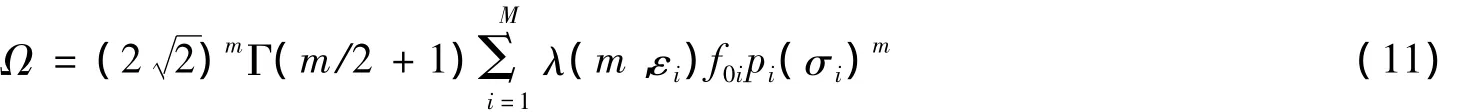
式中:m0和m2为零阶和二阶谱矩;λ(m，εi)为雨流修正因子，用下式表示:

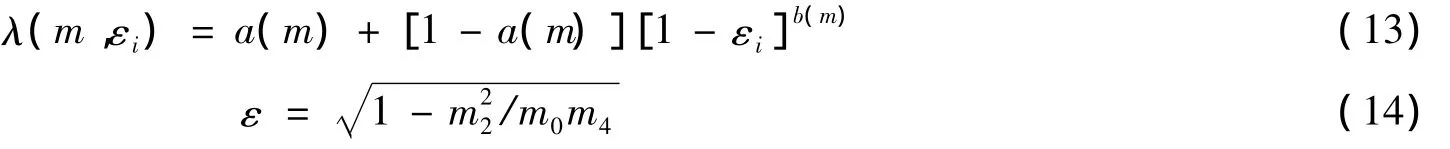
式中:a(m)=0.926-0.033m;b(m)=1.587m-2.323。

断裂力学中疲劳应力参数应根据平台每年在海上运行的实际天数及其所处的海洋环境、结构的类型和动力性能等因素进行计算。平台服役期间假定应力范围的长期分布服从Weibull分布，则应力范围长期分布的概率密度函数为［19］:

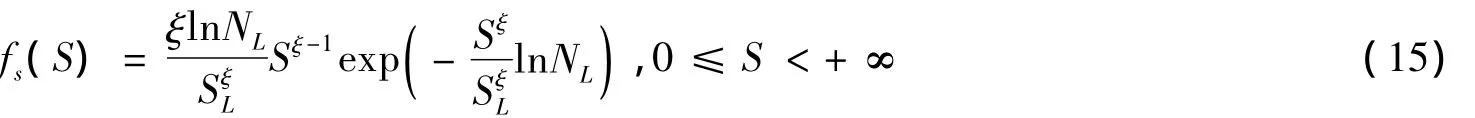
式中:ξ为形状参数;SL为各海况最大应力范围;NL为应力循环总次数。

平台的疲劳应力参数用下式计算:

式中:fL为回复周期L期间应力范围作用的平均频率;Γ为伽玛函数;m为指数。

5 疲劳可靠性的计算结果与分析

应用S-N曲线法和断裂力学方法计算TLP平台立柱与浮箱连接处8个角点和立柱与甲板连接处弦杆与支杆的12个热点的疲劳可靠性指标和失效概率，计算结果如表5和表6所示。立柱与浮箱连接角点的最小可靠性指标分别为3.604和3.410，弦杆与支杆连接处热点的最小可靠性指标分别为3.642和3.427，可以满足设计要求。由于平台的连接部位结构较为复杂，多为焊接连接，不同工况下结构各处的应力响应不同，使得各角点(热点)的可靠性指标大小存在差异。

表5 立柱与浮箱连接处关键角点疲劳可靠性指标和失效概率Tab.5 Probability of failure and fatigue reliability indices of key nodes in column and pontoon

从表5可以看出，平台立柱与浮箱连接处上部角点的疲劳可靠性指标低于下部角点的疲劳可靠性指标，即其上部角点的疲劳失效概率高于下部角点的疲劳失效概率。表6中外支杆Pipe1和Pipe4与弦杆连接处的疲劳可靠性指标低于内支杆Pipe2和Pipe3与弦杆连接处的疲劳可靠性指标，表明外支杆与弦杆连接处容易发生疲劳。疲劳可靠性指标最小的热点是平台最危险的节点，平台服役时应特别关注平台立柱与浮箱连接处上部角点和弦杆与外支杆连接处的疲劳变化，需要加强相应节点连接处焊缝的定期检测，以保证平台结构的安全可靠运行。

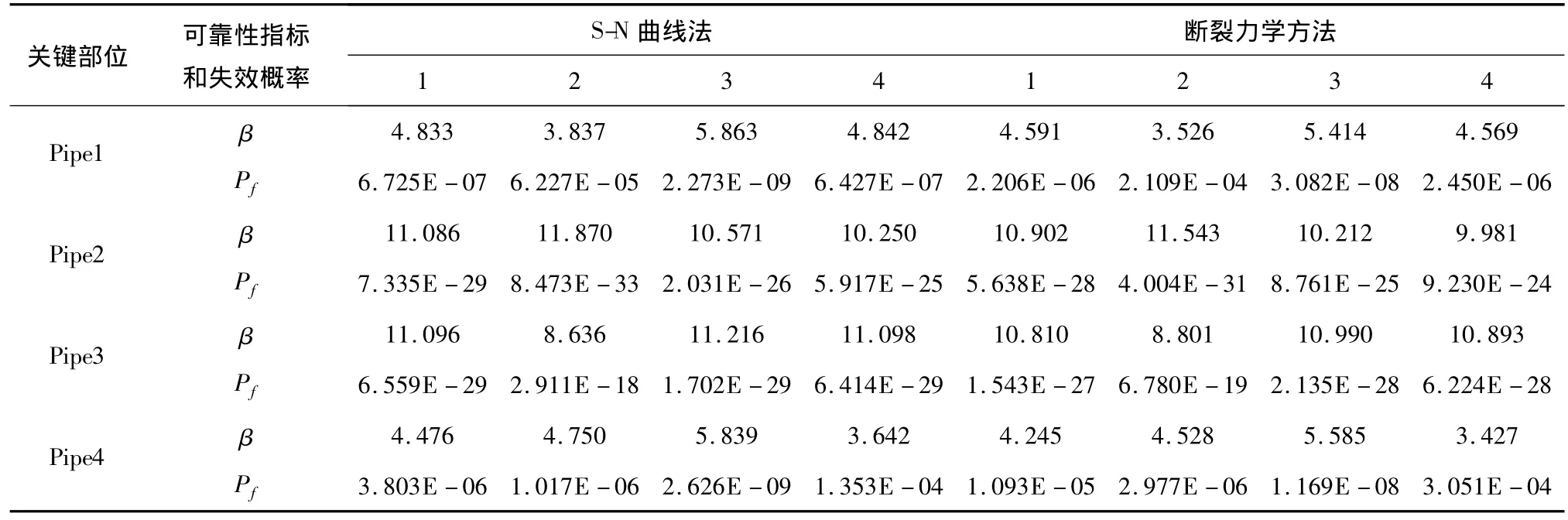
表6 立柱与甲板连接处关键节点的疲劳可靠性指标和失效概率Tab.6 Probability of failure and fatigue reliability indices of key nodes in column and deck

对比表5和表6计算结果可以看出，应用断裂力学方法计算得到的各关键节点疲劳可靠性指标与应用S-N曲线法计算得到的疲劳可靠性指标接近，疲劳可靠性指标的最小值出现在相同的部位，表明分析结果比较合理，可以将两种方法用于TLP平台的疲劳可靠性研究。

6 结语

1)建立了TLP平台整体模型，结合中国南海海况，计算了波浪荷载。分析了不同工况下TLP平台的应力响应，确定了甲板和立柱连接部位、立柱和浮箱连接部位为平台疲劳分析的关键部位。建立了相应的中间局部模型和精细子模型，采用子模型技术，运用几何应力外插法得到了各热点应力幅值。

2)应用S-N曲线法和断裂力学方法分析了TLP平台关键部位的疲劳可靠性，给出了不同工况下疲劳关键部位各热点的疲劳可靠性指标。平台立柱与浮箱连接处上部角点的疲劳可靠性指标低于下部角点的疲劳可靠性指标，外支杆与弦杆连接处的疲劳可靠性指标低于内支杆与弦杆连接处的疲劳可靠性指标。平台服役时需加强相应节点连接处焊缝的定期检测和维修，以保证平台结构的安全可靠运行。

3)通过两种方法的对比分析，应用断裂力学方法计算得到的疲劳可靠性指标与应用S-N曲线法计算得到的疲劳可靠性指标接近，且疲劳可靠性指标的最小值出现在相同的部位，表明分析结果合理，可以将两种方法用于TLP平台的疲劳可靠性研究。

［1］ Kjerengtroen L，Wirsching P H.Structural reliability analysis［J］.ASCE，J.Struct.Eng.，1984，110(7):1495-1511.

［2］ Hove G O，Moan T.Fatigue and fracture reliability of TLP tether system before and after tether failure［C］∥Proc.of the Seventh ICASP.Applications of Statistics and Probability.1995，1(1):319-326.

［3］ Hovde G O，Moan T.Fatigue reliability of TLP tether systems［J］.Journal of Offshore Mechanics and Arctic Engineering Transactions of the ASME，1997，119(1):53-60.

［4］ Ximenes M C C.Fatigue reliability and inspection of TLP tendon system［J］.Marine Technology，1991，28(2):99-110.

［5］ Siddiqui N A，Ahmad S.Reliability analysis against progressive failure of TLP tethers in extreme tension［J］.Reliab.Eng.Syst.Saf.，2000，68(3):195-205.

［6］ Siddiqui N A，Ahmad S.Fatigue and fracture reliability of TLP tethers under random loading［J］.Mar.Struct.，2001，14(3):331-352.

［7］ Khan R A，Siddiqui N A，Naqvi S Q A，et al.Reliability analysis of TLP tethers under impulsive loading［J］.Reliab.Eng.Syst.Saf.，2006，91(1):73-83.

［8］ 张剑波.半潜式钻井船典型节点疲劳可靠性分析［J］.船舶工程，2006，28(1):36-40.

［9］ 马网扣，王志青，张海彬.深水半潜式钻井平台节点疲劳寿命谱分析研究［J］.海洋工程，2008，26(3):1-8.

［10］邓 鹏，颜勇剑，田其磊，等.半潜式平台关键点的疲劳可靠性分析［J］.造船技术，2009(6):15-18.

［11］ Torng T Y，Wirsching P H.Fatigue and fracture reliability and maintainability process［J］.ASCE，J.Struct.Eng.，1991，117(12):3804-3822.

［12］ Kung C J，Wirsching P H.Fatigue and fracture reliability and maintainability of TLP tendons［J］.ASME，Safety and Reliability，1992，1(2):15-21.

［13］ Jiao G Y，Moan T.Reliability-based fatigue and fracture design criteria for welded offshore structures［J］.Eng.Fract.Mech.，1992，41(2):271-282.

［14］ ABS，Guide for the Fatigue Assessment of Offshore Structures［S］.New York:American Bureau of Shipping，2003.

［15］ Paris P C，Erdogan F.A critical analysis of crack propagation laws［J］.J.Basic Eng.，1963，85(4):528-534.

［16］ ABS，Guidance Notes on Spectral-based Fatigue Analysis for Floating Offshore Structures［S］.New York:American Bureau of Shipping，2005.

［17］ DNV，Structural Reliability Analysis of Marine Structures(Classification Nnotes-NO.30.6)［S］.Norway:Det Norske Veritas，1992.

［18］ DNV，Fatigue Design of Offshore Steel Structures［S］.Norway:Det Norske Veritas，2010.

［19］胡毓仁，李典庆，陈伯真.船舶及海洋工程结构疲劳可靠性分析［M］.哈尔滨:哈尔滨工程大学出版社，2010.

［20］ Guedes Soares C，Moan T.Model uncertainty in the long-term distribution of wave-induced bending moments for fatigue design of ship structures［J］.Mar.Struct.，1991，4(4):295-315.

［21］ Moan T.Fatigue reliability of marine structures，from the alexander kielland accident to life cycle assessment［J］.Int.J.Offshore Polar Eng.，2007，17(1):1-21.

［22］ Newman J C，Raju I S.An empirical stress-intensity factor equation for the surface crack［J］.Eng.Fract.Mech.，1981，15(1-2):185-192.

［23］ BS7910，Guide to Methods for Assessing the Acceptability of Flaws in Metallic Structures［S］.London:British Standards Institution，2005.