交错布置对高频变压器绕组损耗的影响

房 岩，周洁敏

(南京航空航天大学民航学院，南京211100)

在设计开关电源拓扑的过程中，必不可少的重要环节就是磁性元件的优化设计问题。现代电力电子装置逐渐向小型化发展，减小磁性元件体积的有效方法之一就是提高工作频率，但是随着频率的提高，集肤效应和邻近效应增加了绕组的损耗［1］。与理想变压器不同的是，高频变压器都储存着一些不希望的能量，例如漏感能量。漏感［2］是一个寄生参数，影响电路运行效果并恶化效率。因此在设计变压器时，有必要改变传统的绕组布置方法，改变绕组结构和工艺，达到减少高频损耗和漏感的目的。在对一般高频变压器进行优化设计时，通常采用绕组交错布置方法，文献［3－4］指出，将初级与次级绕组交错布置可以有效减少绕组的漏感和交流损耗。

当变压器次级输出大电流时，如果采用多股细线并绕，会造成填充系数较低;如果采用铜箔绕组，在允许的电流密度和集肤深度下，通常选择绕组并联方式。在低频时，只要保证相同匝数绕组的直流电阻相等，就可以保证电流的均分;但在高频时，所处磁场对称比电阻平衡更为重要。在高频变压器中，全部电流高频分量将在初级与次级直接面对的里层内表面和相邻外表面流动［5］。文献［6］提出绕组并联时合理的布局可有效减少变压器的漏感和交流损耗。

本文采用 Ansoft Maxwell［7］软件构建变压器模型，首先对绕组交错布置时绕组损耗的变化进行了详尽的分析，其次深入研究了绕组并联时交错布置对变压器绕组的影响，最后提出一种有效减少涡流损耗的新模型方案。仿真结果对变压器绕组的合理设计提供了理论依据和技术支持。

1 仿真模型的构建

Ansoft Maxwell 2D电磁场仿真软件基于麦克斯韦微分方程，采用有限元离散形式，在各个工程电磁场领域得到了广泛的应用。

本文依据变压器结构以及电磁场分布的对称性，在分析前作如下设定:

1)由于EE型变压器在结构上的对称性，2D计算模型取整个变压器模型的一半。

2)设定涡流场求解器，分析受涡流、集肤效应和邻近效应影响的系统。

2 高频变压器绕组布置分析

为减少变压器交流电阻损耗，应尽量减少绕组的层数。每层匝数尽量多，要求窗口宽度尽量宽。但是对于EE型磁芯不可能象环形磁芯的窗口宽度那样宽，因此匝数较多时不可避免地需要多层绕制，这时就需要考虑多层绕组的合理排列以减少绕组损耗。变压器绕组交错布置时，初、次级在结构上耦合度提高，磁芯窗口中的磁场能量降低，对应的漏感能量降低;初、次级电流的补偿效应在一定程度上使得导体的电流密度减小，电流在导体内部分布更为均匀，有效降低绕组温升。现利用有限元分析方法，对一个初级流过1．2 A交流电、次级流过12 A交流电、工作频率在200 kHz的铁氧体变压器进行分析。

2．1 绕组布置方式理论分析

图1为变压器绕组布置的4种方案，初、次级均由两层绕组构成。图1中各绕组处于低频磁场场合，P表示初级绕组，S表示次级绕组，“叉”和“点”分别表示不同的电流方向，H表示磁场强度。由图1可以看出绕组交错排列的优势

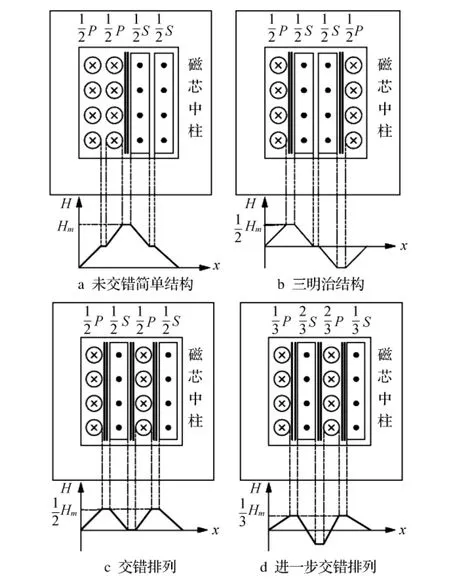
图1 变压器绕组排列的4种方案

1)图1a中，初级磁动势随着安匝数的增加而增大，在初、次级绕组的交界面达到最大值后开始不断减少，在次级绕组外边缘减少到零，产生较大的邻近效应和漏感。

2)图1b为三明治绕组结构，这种结构中最大磁场强度减小，且在绕组中心减少到零，因此有效层数仅为总次级绕组层数的一半。且这种绕制方法减少了一个线圈绝缘和外接线。图1c中磁场强度变化情况与图1b效果相似，可以大大降低漏感和交流损耗。

3)图1d进一步对多层绕组分段绕制。同理，还可以分成(1/3)P－(1/2)S－(1/3)P－(1/2)S－(1/3)P等，最大磁场强度降低到1/9。但是进一步增加交错排列段数对性能改善是有限的，而且随着绕组分段太多，绕制工艺困难，绝缘增加造成屏蔽困难，窗口填充系数降低，层间电容更大。

绕组交错排列时，窗口中最大磁场强度比不交错排列时减小，对应的漏感能量减小，这种效应在高频场合下依然存在。

2．2 绕组布置方式仿真分析

根据上述理论分析，分别对4种方案进行有限元仿真。4种方案的几何模型如图2所示，4种方案的层间磁场强度分布如图3所示(分别以图2几何模型中线为分析路径)，4种方案绕组层间电流密度如图4所示(分别以图2几何模型中线为分析路径)。

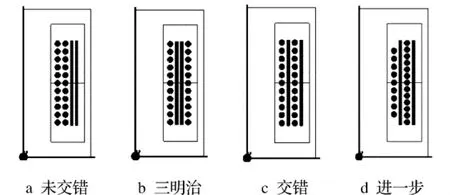
图2 4种方案的几何模型

通过对4个方案的层间磁场强度分析，方案1的最大值约为方案2与方案3的2倍，方案4值略小。图1为低频工作时的理论分析图，当工作频率提高时，磁场强度图略发生变化，但数据走向符合基本理论。需要说明的是，考察路径为变压器中部，且数据都设在第一象限没有负值，因此方案2、方案4的磁场强度图与理论图略有不同。电流密度曲线图中正负值代表电流的流向，电流垂直于纸面向外为正值。绕组未交错排列时，如图3a所示，从最左侧导体层看起，由于邻近效应，电流集中在导线的最右边。对第二层导线进行分析，若导线中没有电流，第一层的交变磁场将在第二层产生涡流损耗，使第二层最左边边缘集肤深度内产生与第一层最右边大小相等方向相反的电流，才能保证第二层中心磁场和电流为零。在第二层最右边初级安匝应全部加在窗口宽度上，在集肤深度内除了和第一层相同的电流外，还要流过第二层最左边相等但方向相反的电流，即在第二层最右边流过两倍第一层同向的电流，还流过与第一层相等但反向的电流，保证静电流仍然与第一层相同。同理，第三、四层即次级绕组电流情况也是这样。比较图3中其他电流密度分布，可见采用交错布置的方法窗口漏磁场减小，绕组电流密度最大值也减小，绕组受邻近效应的影响也减小。以方案2为例，绕组方式(1/2)P－(1/2)S－(1/2)S－(1/2)P，从仿真图4中可以清楚看出，在一、次级绕组之间靠近的地方电流密度最大，然后向外呈指数下降，这是由于考虑了集肤效应与邻近效应的关系，使得导体电流挤在两导体接近的一边。对于多层线圈来说，导线直径为几倍集肤深度时，导线内部存储能量很少或没有，高频时减少了漏感，但是损耗增加太多，邻近效应比集肤效应引起更严重的交流损耗。图5的涡流损耗值数据说明采用绕组交错技术，降低了最大磁场强度和空间磁场能量，也大大降低了绕组的涡流损耗。方案2、方案3和方案4的数据表明，进一步增加交错段数对性能的改善是有限的，一般采用三明治结构，便可获得满意结果。

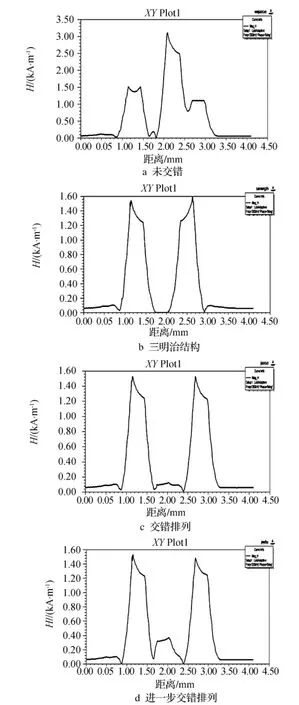
图3 4种方案的磁场强度曲线图

图4 4种方案的电流密度曲线图

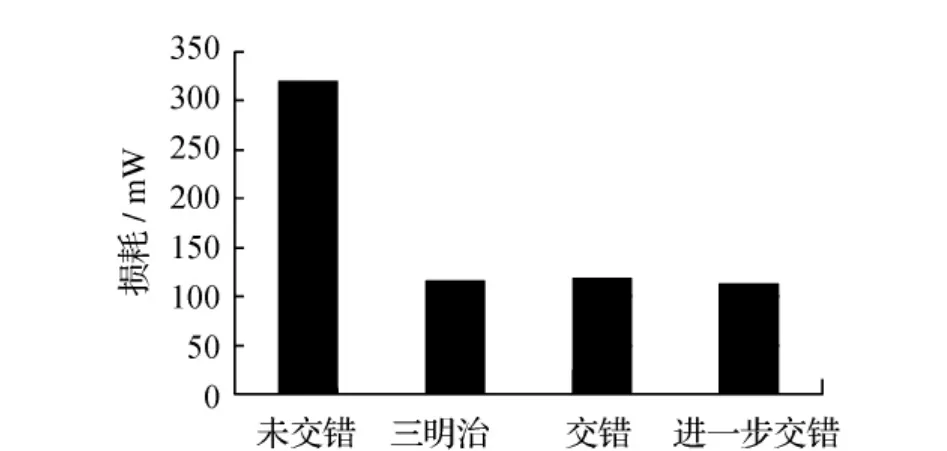
图5 4个方案的涡流损耗值

3 绕组并联布置方式

根据上述分析，绕组交错布置有效减小了涡流损耗，改善了导体中电流分布，减少了邻近效应的影响。为了减少并联绕组的交流损耗，仍可采用交错布置方法，达到并联绕组的均流优化设计。现利用有限元分析方法，对一个初级流过1．6 A交流电、次级流过12．8 A交流电、工作频率在200 kHz的变压器进行分析。分别建立4种方案的几何模型。方案1为传统简单并联情况，初、次级侧绕组分别为2层，初级绕组每匝4股并绕，次级绕组为2条铜箔并联。方案2为交错并联，在方案1的基础上将初、次级绕组交错排列。方案3是将方案2中的初级绕组并联的4根导线分开放置，2根放置在第一层上，另2根放置在另一层上，次级绕组不变。方案4提出一种新型模型，将初级4根并联导线分别放置在3层上面，布置为1－2－1结构。

4种方案的仿真几何模型如图6所示，层间磁场强度如图7所示(分别以图6几何模型中线为分析路径)，绕组电流密度如图8所示(分别以图6几何模型中线为分析路径)。

通过对以上涡流场的仿真结果分析可知:

1)方案1的层间磁场强度约最大值约为1．18 kA/m，方案 2 约为 0．78 kA/m，方案 3 约为0．59 kA/m，方案 4约为 0．58 kA/m。方案 1为传统的并联绕组结构，交错绕制结构的层间磁场强度最大值要比传统模型小很多，且各绕组间磁场强度分布更为均匀。

图6 4个方案的几何模型

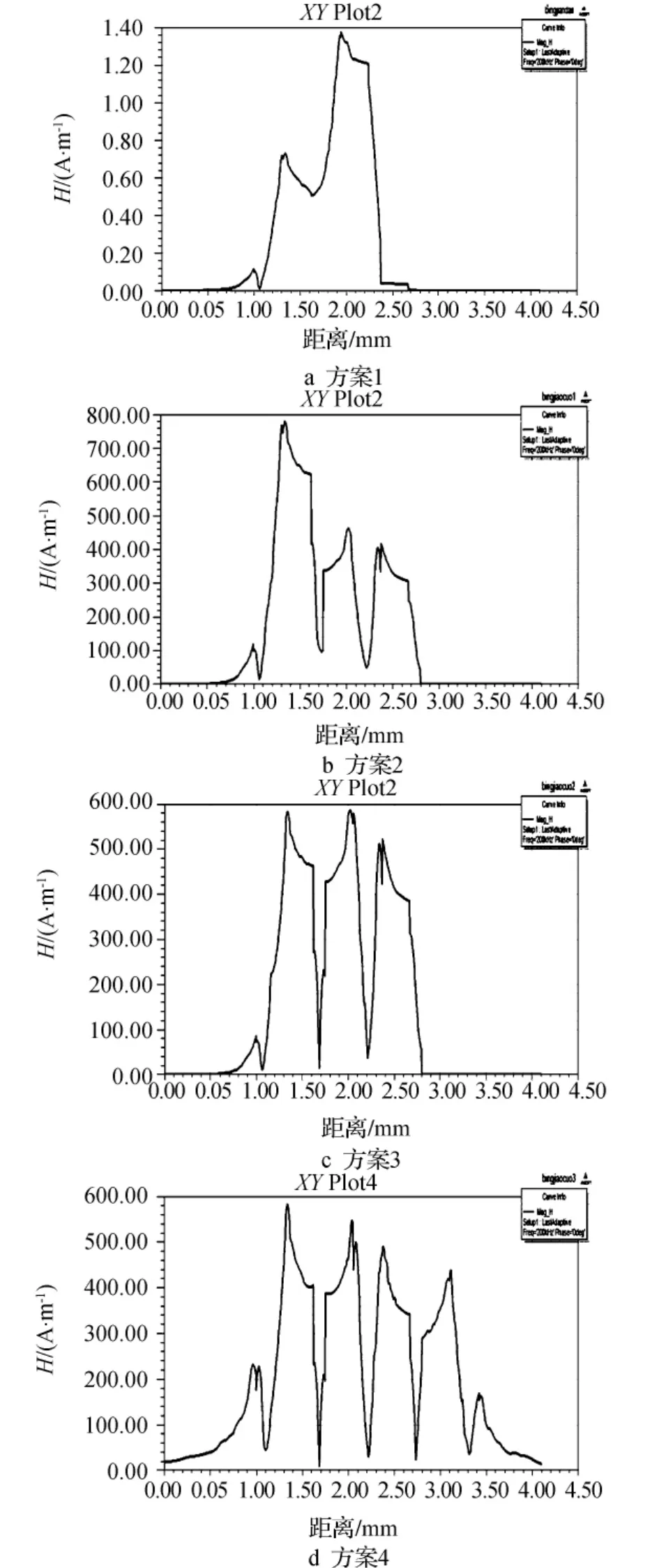
图7 4种方案的层间磁场强度曲线图

图8 4种方案的电流密度曲线图

2)传统并联绕制方法的电流在高频条件下分布极其不均匀，最大值几乎是最小值的10倍，二次侧最右边铜带中电流密度值很小，增加了绕组的交流阻抗，造成很大的涡流损耗，增加温升。温升过大时会影响变压器的使用寿命，对周围的元器件也造成影响。通过交错排列技术能有效改善电流密度的不均匀分布，减小邻近效应的影响。经过进一步的交错排列，观察图8d新模型方案，各层绕组电流密度分布已很均匀，每层绕组内电流密度变化较小。图9中4种方案的涡流损耗值也说明了这一结论，新模型并联均流方案各项性能指标优于传统模型，更有利于减小涡流损耗。

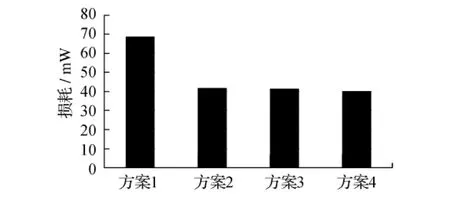
图9 4个方案的涡流损耗值

4 结束语

本文针对高频变压器中传统绕组布置方法交流损耗和漏感大的缺点，分析了变压器绕组不同布置方式的特点，得出交错布置为最优方案，并将此方法应用于绕组并联模型中，获得新的并联均流方案。经电磁场有限元分析方法验证，该方法有效且可行。

［1］旷建军，阮新波，任小永．集肤和邻近效应对平面磁性元件绕组损耗影响的分析［J］．中国电机工程学报，2006，26(5):170－175．

［2］周洁敏．开关电源理论及设计［M］．北京:北京航空航天大学出版社，2012．

［3］DAI N，LEE F C．High－frequency eddy－current effects in low － profile transformer windings［J］．Proc．IEEE PESC．1997:641－647．

［4］DAI N，LOFTI A W，SKUTT C，et al．A comparative study of high－frequency，low－profile planar transformer technologies［J］．Proc．IEEE APFC．1994:226 －232．

［5］赵修科．开关电源中磁性元器件［M］．南京:南京航空航天大学出版社，2004．

［6］吴海波，孟明，樊长在．正激式高频变压器层内绕组布置分析［J］．黑龙江电力，2012，34(2):107－112．

［7］赵博．Ansoft 12在工程电磁场中的应用［M］．北京:中国水利水电出版社，2010．