动态连续潮流与改进粒子群优化算法相结合的静态电压稳定分析

薄明明，安 亮

(1.东北电力大学 电气工程学院，吉林 吉林132012;2.吉林供电公司继电保护所，吉林吉林132012)

近年来，世界上许多大电网相继发生了以电压崩溃为特征的严重事故，这些电力系统事故都造成了巨大的经济损失和严重的社会秩序紊乱，使得电压稳定问题引起了电力界的普遍关注［1-4］。因此，实时掌握系统的电压稳定情况，提高电力系统电压稳定性，对维持电网安全运行具有重要意义。

目前静态电压稳定分析的方法有灵敏度分析法、潮流多解法、最大功率法、奇异值分析法、崩溃点法、连续潮流法、动态连续潮流法、非线性规划法等。连续潮流法由于能考虑一定的非线性控制及不等式约束，能绘制出完整的PV曲线，且计算得到的功率裕度能较好反映系统的电压水平，已被广泛应用于静态电压稳定分析［5-8］。但连续潮流法也存在一些不足［9］:功率的传输方向因平衡点选择不同而发生改变，使得计算结果依赖于平衡点的选择，尤其是在系统负荷加重甚至接近电压崩溃点时这一现象更加明显。因此应采用连续潮流法的改进方法(动态连续潮流法)进行静态电压稳定裕度计算。

变压器分接头的位置、发电机机端电压和并联电容器组的投切容量等控制变量对电压稳定裕度的计算结果影响很大，其中变压器分接头的位置和并联电容器组的投切容量又是离散变量。如何调节控制变量以求取最大静态电压稳定裕度，是一个非线性规划问题。常规算法求解最大静态电压稳定裕度的主要困难是离散变量的归整、多峰多极值问题。近年来新兴的人工智能算法逐渐得到重视，如遗传算法(GA)、鱼群算法(AFSA)、蚁群算法(ACO)、粒子群算法(PSO)，这些人工智能算法具有并行处理的特征，易于实现，但存在计算速度慢、易陷入局部最优解等缺点。

自适应混沌聚焦粒子群算法(ACFPSO)是根据粒子群算法全局搜索和局部搜索平衡特性，对初始粒子进行混沌操作以提高初始粒子质量而得到的具有较好全局搜索能力和寻优速度的改进人工智能算法。本文建立了分析静态电压稳定的优化模型，介绍了动态连续潮流与自适应混沌聚焦粒子群算法相结合的求取系统最大静态电压稳定裕度的方法。

1 分析静态电压稳定的优化模型

1．1 动态连续潮流方程

动态连续潮流与连续潮流主要的不同在于:不平衡功率由所有节点根据节点的发电机和负荷静态频率特性共同承担;平衡点发电机的功率也应事先给定。

系统中不平衡功率为

式中:λ是描述系统负荷增长的参数，简称负荷参数，在连续潮流方程中λ满足0＜λ＜λcr，λ=0对应系统的基态负荷水平，λ=λcr对应系统在电压崩溃点的负荷水平;x为系统的静态状态向量(本文取直角坐标故为电压的实部和虚部);x0为基态时系统的静态状态向量。

频率偏移为

式中:KGi、KLi分别为发电机和负荷的单位调节功率。在求取电压稳定裕度的同时也可以对系统的频率进行监视。

输电系统网损有功功率在数值上等于系统中全部节点注入有功功率的代数和，用节点电压和导纳表达的线损功率公式为

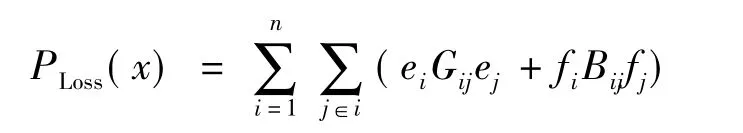
动态连续潮流方程表达式为

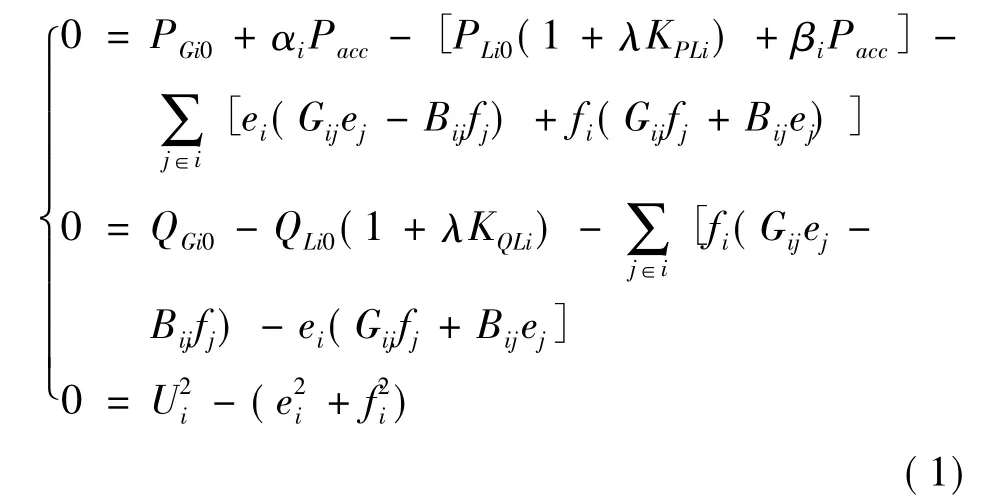
式中包括平衡点的有功方程，PGi0、QGi0为基态时i节点发电机发出的有功和无功，PLi0、QLi0为基态时i节点的负荷，KPLi、KQLi为i节点负荷的增长系数(一般取恒功率因数的增长方式KPLi=KQLi)。αi、βi是根据节点i发电机和负荷的静态频率特性分担不平衡功率的系数:

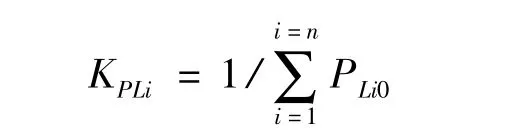
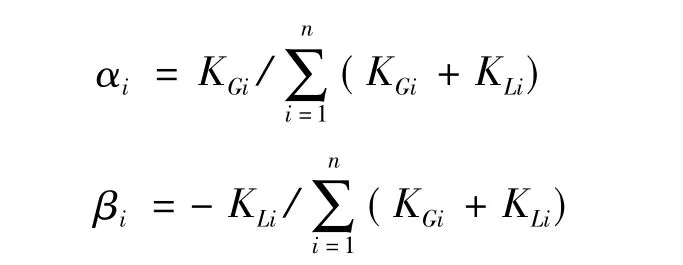
为描述方便，式(1)可简化为

如果考虑控制变量ρ，式(2)可以进一步表示为

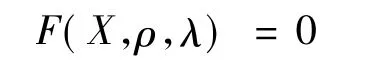
动态连续潮流与连续潮流的未知数个数相同，平衡点(isb)有功方程并不需要参与迭代计算，其求解过程与连续潮流相似，不同的是由于网损增量的引入将破坏原雅克比矩阵的稀疏性［9］。为了利用原潮流雅克比矩阵的稀疏性，本文采用直接修正有功失配量法，即把第i－1步的网损增量看作是第i步的网损增量:

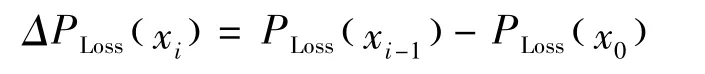
1．2 分析静态电压稳定裕度的优化数学模型

静态电压稳定裕度是静态电压稳定性分析的一个重要指标，是指从当前运行点出发，不断增加系统负荷直至发生电压崩溃，崩溃点到当前运行点的距离。优化目标是通过调节控制变量ρ使静态电压稳定裕度取得最大，故将系统的静态电压稳定裕度最大作为目标函数，即

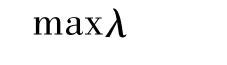
等式约束条件为

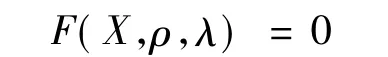
状态变量的不等式约束为

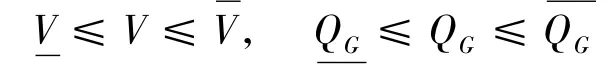
控制变量的不等式约束为

采用精确罚函数法处理PQ节点电压和发电机的无功出力这两个状态变量的不等约束［10-11］，则目标函数可以表示为

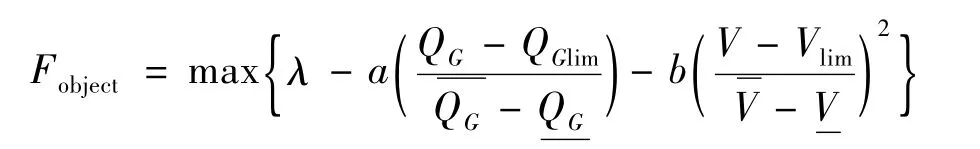
式中，a、b分别为对发电机无功出力越限的惩罚项的惩罚系数和对PQ节点电压越限的惩罚项的惩罚系数。其中

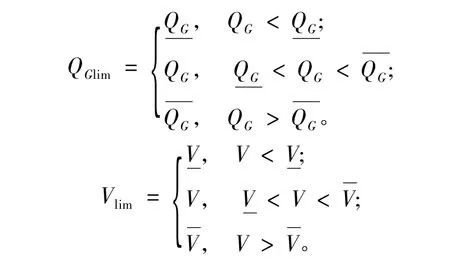
2 基于改进粒子群优化算法的最大静态电压稳定裕度求取

2．1 ACFPSO算法的基本原理

由于AFPSO算法中初始粒子是随机生成的，并不能保证每个粒子的质量，粒子的质量影响AFPSO算法的寻优速度。为提高初始粒子的质量将具有随机性和遍历性的混沌算法引入到粒子群算法中［12］，对随机生成的初始粒子群进行混沌操作，然后按适应值f(静态电压稳定裕度值)的大小排序，选取f排在前m(种群规模)的进行迭代寻优。

混沌操作过程为

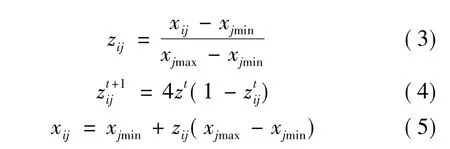
式中:Zi为与Xi对应的混沌粒子，xjmin、xjmax为控制变量的下限值和上限值，t为进行混沌操作的次数。

粒子群参数采用自适应策略，对性能较好的粒子采用较大的惯性权重w和加速系数c1、c2让其负责更优区域的探索。对性能较差的粒子采用较小的w和c1、c2，让其迅速收敛到较好的区域进行细致搜索。同时，当搜索结果好于当前粒子个体极值时，保持该个体的当前速度继续向前搜索，使粒子不必频繁更新速度，这有利于提高良好速度信息的利用率，减小算法的计算量，加快运算的收敛速度。此外，使个体始终保持自己搜索过程中的极值位置并以此为起点进行后续搜索，起到“聚焦”作用［13］。

该策略是将粒子按其个体最优从优到劣进行排序，排在第i位的粒子个体最优值记为fpi，惯性权重及相应加速系数为

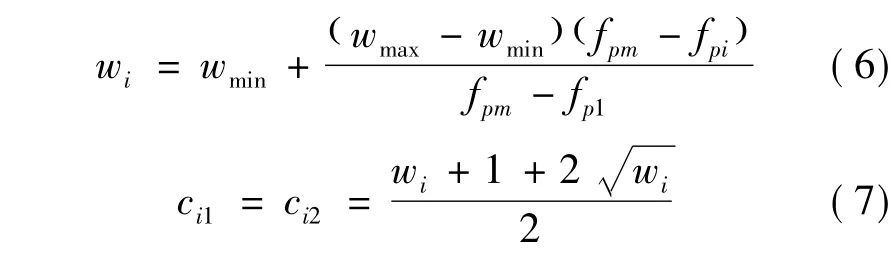
式中:wmax、wmin分别为最大和最小惯性常数。

粒子的速度和位置按下式更新:

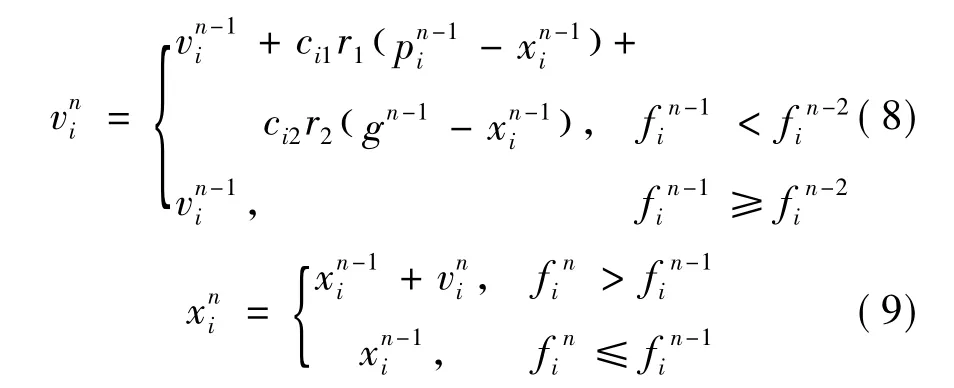
式中:i为粒子的编号i=1，2，…，m;n为迭代次数，n=1，2，…，trymax;r1、r2为(0，1)之间的随机数;g为全局最优点。

2．2 最大静态电压稳定裕度的求取

用ACFPSO算法求取最大静态电压稳定裕度的步骤如下:

1)输入原始数据，初始化种群中粒子(一组控制变量)的位置和速度，给定最大速度vmax，位置边界Xmin、Xmax和混沌操作次数k。

2)对各个初始粒子按式(3)-(5)进行混沌操作，并用动态连续潮流法计算其对应的适应值f，降序排序取排在前m的f对应的m个粒子。设排在第i位的这个粒子序号为i，是当前的个体最优位置pi，排序排在第一位的就为全局最优位置g。

3)根据式(6)、(7)计算每粒子的惯性权重和加速系数。

4)根据式(8)、(9)更新速度和位置，计算新生成的m个粒子的适应值，并据此更新个体最优位置及对应的适应值。

5)将每个粒子的个体最优从优到劣进行排序、编号。

6)t=t+1，判断是否已达最大迭代次数trymax，若是，则输出最大静态电压稳定裕度fg(fg=fp1);否则转至步骤3)。

3 算例分析

为验证动态连续潮流与改进粒子群优化算法相结合求取静态电压稳定裕度这种方法的有效性，采用Matlab2008分别对IEEE6、IEEE30标准节点系统进行计算，并将结果与连续潮流法和基本粒子群优化算法等进行比较。

3．1 动态连续潮流与连续潮流的比较

以IEEE30节点系统为例，各负荷节点保持功率因数不变按基态负荷比例增长，连续潮流中各发电机节点按基态发电机出力比例增加出力，动态连续潮流中各节点的发电机和负荷根据静态频率特性进行调整。

为了使得当选择的平衡点不同时，计算的约束条件相同，假设系统中所有发电机出力不受限制，各发电机的单位调节功率大小相同KG*=30。

图1给出了选择不同发电机节点作为平衡节点isb，分别用连续潮流法和动态连续潮流法计算得到的静态电压稳定裕度结果。由图1可以看出:用连续潮流法计算静态电压稳定裕度的结果随所选择的平衡点的不同而不同。选择节点8为平衡节点时静态电压稳定裕度最大λcr=1．729 1，选择1节点为平衡节点时静态电压稳定裕度最小λcr=1．579 0 。

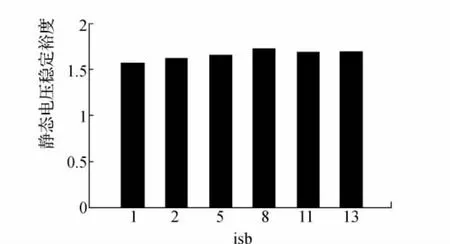
图1 IEEE30节电系统连续潮流法选择不同平衡节点的电压稳定裕度

同样的负荷增长方式，采用动态连续潮流法计算选择不同平衡点时的静态电压稳定裕度，并将其与连续潮流的进行比较，结果如图2所示。

由图2可以看出:连续潮流法计算的电压稳定裕度随平衡点选择的不同而不同，而动态连续潮流法计算的结果始终不变λcr=1．6774，即不依赖于平衡点的选择。

图2 IEEE30节点系统2种方法下选择不同平衡节点计算的电压稳定欲度

3．2 最大电压稳定裕度计算

为验证本文所提出方法的有效性，对IEEE6和IEEE30进行仿真计算，取误差精度pr=10－6，a=1．5，b=2．0，wmin=0．4，wmax=0．9，最大迭代次数trymax=100，6节点系统种群数取20，30节点种群数取30，独立运行10次取平均值，其结果如表1-表4所示。

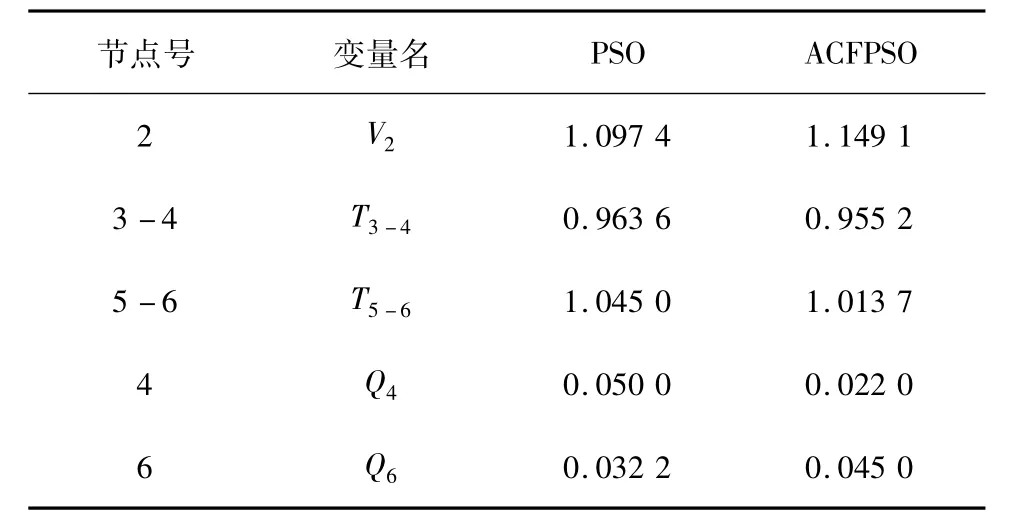
表1 IEEE6节点系统控制变量最优解 p.u.

表2 IEEE6节点系统的最大静态电压稳定裕度p.u.

从表1和表2可看出，粒子群优化算法和自适应混沌聚焦粒子群优化算法搜索得到的最优控制变量平均值有所不同，后者搜索到的最优控制变量下取得的最大静态电压稳定裕度大。因此通过本文所提出的方法可以得到更好的提高静态电压稳定裕度的控制措施。

由表3和表4可以看出:用自适应混沌聚焦粒子群优化算法搜索得到的最优控制变量对应的静态电压稳定裕度大于其他方法。进一步说明了本文所提出的算法在最大静态电压稳定裕度求解上的有效性和优越性。

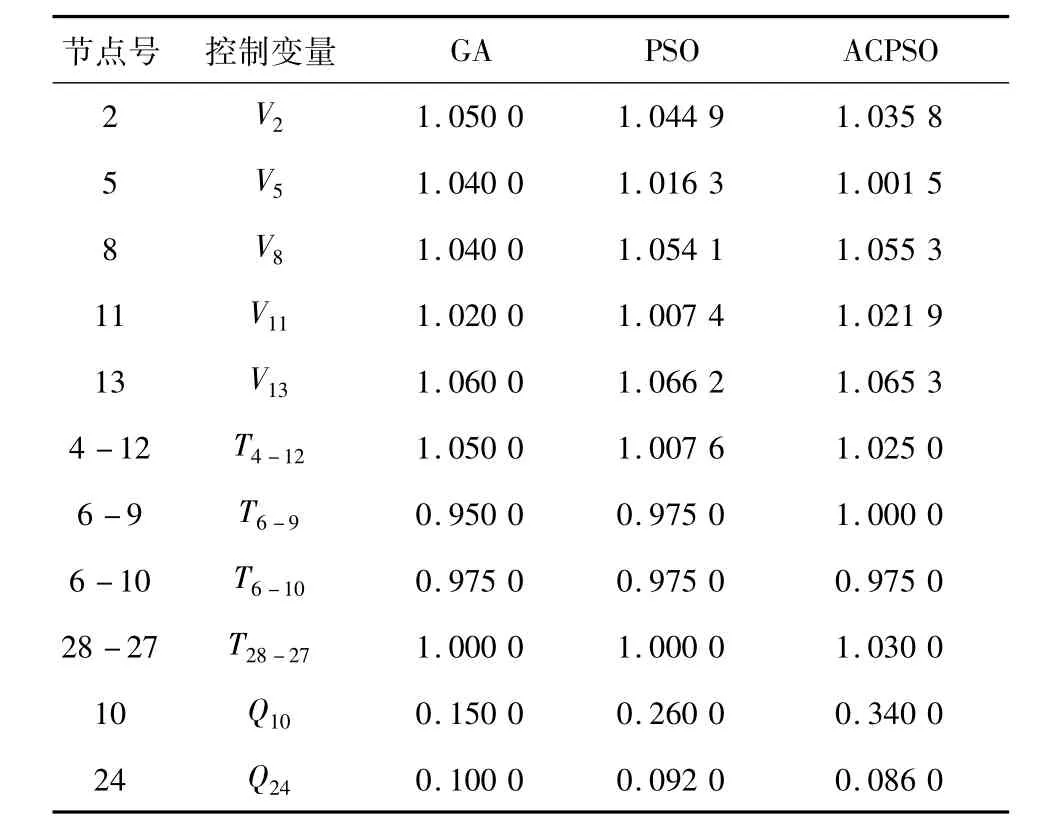
表3 IEEE30节点系统控制变量最优解 p.u.

表4 IEEE30节点系统最大静态电压稳定裕度p.u.

3．3 PSO、和ACFPSO算法的收敛性比较

在对IEEE30节点系统进行仿真时，用计时函数cputime分别计算用PSO、AFPSO和ACFPSO算法求最大电压稳定裕度迭代到每一次所需要的时间，直至trymax=100，生成电压稳定裕度与程序运行时间的曲线，如图3所示。

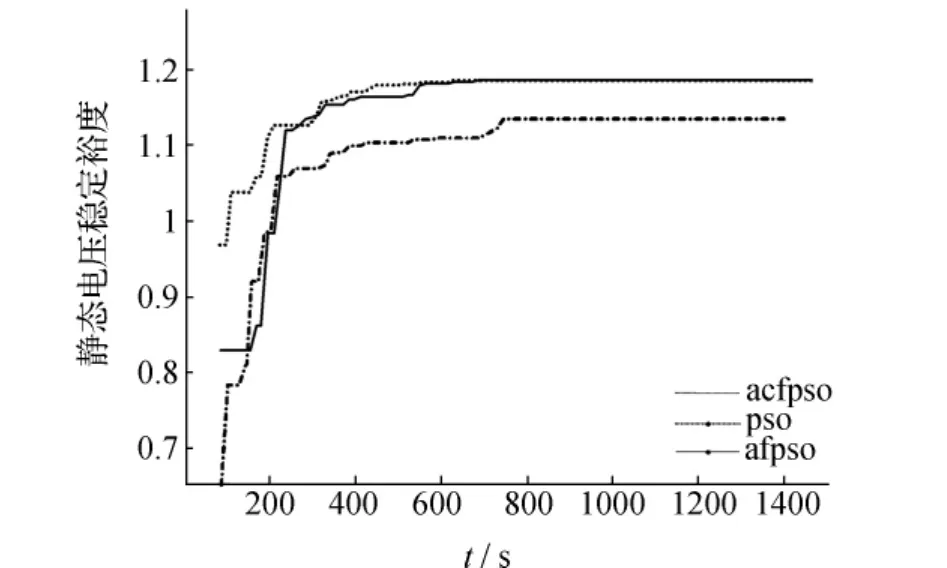
图3 IEEE30节点系统3种算法下不同时刻的电压稳定裕度

由图3可看出，用ACFPSO算法计算电压稳定裕度的收敛速度更快，且保持了AFPSO较好的全局寻优能力。由此可见，本文所提出对PSO算法的改进方法的确提高了PSO算法的性能。

4 结束语

建立了新的分析系统静态电压稳定的优化模型，采用精确罚函数法处理状态变量不等式约束，使计算结果更符合实际。其中用动态连续潮流计算每组控制变量对应的静态电压稳定裕度的方法，根据发电机和负荷静态频率特性分配系统中的不平衡功率，克服了分析结果因平衡点选择的不同而不同这一现象，提高了静态电压稳定分析的精度。

ACFPSO算法通过改善初始粒子的质量，对粒子群参数采用自适应策略和调整粒子群速度、位置的更新策略，进而得到的一种具有较好全局搜索能力和寻优速度的人工智能算法。

［1］印永华，郭剑波，赵建军，等.美加“8.14”大停电事故初步分析以及应吸取的教训［J］.电网技术，2003，27(10):8-11.

［2］刘鹏，吴刚.世界范围内两起典型电压崩溃事故分析［J］.电网技术，2003，7(5):35-37.

［3］李再华，白晓民，丁剑，等.西欧大停电事故分析［J］.电力系统自动化，2007，31(1):1-4.

［4］唐葆生.伦敦南部地区大停电及其教训［J］.电网技术，2003，27(11):1-5.

［5］赵晋泉，张伯明.连续潮流及其在电力系统静态稳定分析中的应用［J］.电力系统自动化，2005，29(11):91-97.

［6］祝大康，程浩忠.求取电力系统PV曲线的改进连续潮流法［J］.电网技术，1999，23(4):37-40.

［7］王成山，魏炜.一种改进的步长控制连续性潮流计算方 法［J］.电工技术学报，2004，19(2):58-63.

［8］李娟，陈继军，司双.连续潮流与免疫遗传算法结合的静态电压稳定裕度计算［J］.电力系统保护与控制，2010，38(18):24-27.

［9］孙宏斌，李钦，张明晔，等.基于动态潮流方程的连续潮流模型与方法［J］.中国电机工程学报，2010，31(7):77-82.

［10］胡彩娥.应用基于连续潮流算法的遗传算法进行静态电压稳定分析［J］.电网技术，2004，28(15):57-61.

［11］聂宏展，张冰冰，王新，等.基于改进粒子群优化算法的电力市场下的无功优化［J］.电网技术，2007，31(21):85-90.

［12］李娟，杨琳，刘金龙，等.基于自适应混沌粒子群优化算法的多目标无功优化［J］.电力系统保护与控制，2011，39(9):26-31.

［13］刘述奎，陈维荣，李奇，等.基于自适应聚焦粒子群优化算法的电力系统多目标无功优化［J］.电网技术，2009，33(13):48-53.