基于相对核的属性约简

王健，徐余法，陈国初

（1.华东理工大学 信息科学与工程学院，上海200237；2.上海电机学院 信息学院，上海200240）

1982年，波兰数学家Pawlak提出了粗糙集［1］，这是一种定量分析处理不一致、不完整、不精确的信息与知识的数学工具和一种重要的信息处理技术［2-5］.粗糙集的理论是建立在分类机制的基础上，将知识理解为对数据的划分.粗糙集理论与其他处理不确定和不精确问题理论［6-7］的最显著的区别是，它无需提供问题所需处理的数据集合之外的任何先验信息，所以对问题的不确定性的描述或处理可以说是比较客观的［8-9］.因此，被广泛应用到人工智能、模式识别和数据挖掘等方面.粗糙集理论研究课题中一个重要的内容就是属性约简.一般说来，知识库中的属性的重要度并不是相等的，有些属性可以删除，从而有利于做出正确而简洁的决策.属性约简可以在保持分类和决策能力不变的情况下，去除那些不相关或不重要的属性.Wong等［10］从计算复杂性的角度证明了寻找最小约简是NP-hard问题，通常采用启发式的搜索算法［11-17］.本文从相对核的角度，提出了一种新的属性约简方法.

1 粗糙相关概念

粗糙集的关键点就是将知识和分类联系起来，用等价类关系的形式表示分类［18］.

定义1 决策表 .一个决策表可以形式化定义为S＝〈U，C∪D，V，f〉.其中：有限集合U＝｛u1，u2，…，un｝为论域；C∪D是属性有限集，C为条件属性集，D为决策属性集，且C∩D＝Ø；V为属性集C∪D的值域；f∶U×C∪D→V为一个信息函数，表示任一个对象的属性在V上的取值，指定了U中每一对象x的属性值.

定义2 不可分辨关系.信息系统S＝〈U，C∪D，V，f〉，对于属性子集B⊆A，定义一个不可分辨的二元关系.即IND（B）＝｛（x，y）∈U×U∶∀a∈B，f（x，a）＝f（y，a）｝.IND（B）是一个等价关系.由这种等价关系导出的对U的划分记为U／IND（B），其中包含x的等价类记为［x］IND（B）.

定义3 近似集合 .粗糙集有两个基本概念，即上近似集和下近似集，给定X⊆U，R⊆A.

1）下近似集，即R-X＝∪｛［x］R⊆X｝，［x］R＝｛y｜y∈U，∀a∈R，f（x，a）＝f（y，a）｝.R-X是由U上在现有知识R的划分下肯定属于X的元素组成的集合.

2）上近似集，即R-X＝∪｛［x］R∩X≠Ø｝.R-X是在知识R划分下可能属于X的元素组成集合.

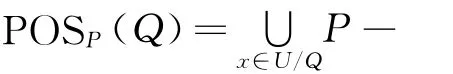
定义5 相对核 .设属性a∈C，如果POSC-a（D）＝POSC（D），那么称属性a相对决策属性D是不可缺少的，所有不可缺少的属性构成了相对决策属性D的相对核.

2 属性约简算法

2.1 算法描述

对于一个信息系统，S＝〈U，C∪D，V，f〉，求出条件属性相对决策属性的相对核，并用这些相对核属性对论域U进行划分 .划分后，将可以正确辨识的部分去掉，并从条件属性中去除这些核属性，这样就形成新的决策信息系统 .然后，不断地迭代，直到论域U完全划分，即U＝Ø.假如某一次迭代的过程中不存在相对核属性，则根据属性重要度，选择对划分重要度最大的属性，并用该属性对当前的论域进行划分.当U＝Ø时，求取每步相对核或重要度最大的属性的并集，假设集合为P＝｛a1，a2，…，am｝，计算POSP（D）和POSP-ai（D）（i＝1，2，…，m），去除冗余信息，得到约简集.

非核属性的属性重要性的判断.文中假如某一步不存在相对核属性，那么要从剩余的属性中选取属性重要度大的属性，来对当前的论域进行划分.设属性a为条件属性，那么定义属性a的重要度为

Siga越大，则该属性的重要度越大.

2.2 算法部分

输入：决策信息系统S＝〈U，C∪D，V，f〉，A＝C∩D，C为条件属性，D为决策属性.输出：决策信息系统的约简 .初始化：集合P＝Ø.算法有如下6个主要步骤：

步骤1 求出决策信息系统的相对核CORED（C），记Q＝CORED（C），若CORED（C）＝Ø，则转步骤4；

步骤2 用相对核对论域U进行划分，若能将论域U完全划分则转步骤5；否则，会有不可辨识的部分，记为U1，U1＝U-POSQ（D），P＝P∪CORED（C），U＝U1；

步骤3 令C＝C-CORED（C），然后转步骤1；

步骤4 利用式（1）计算剩余属性的重要度，并排序.选取重要度最大的属性，假设为a，P＝P∪a；然后用属性a对当前的论域进行划分，若能完全划分，则转步骤5；否则，记不可分别的部分为U2，U2＝U-POSa（D），U＝U2，C＝C-｛a｝，转步骤1；

步骤5 对P中的每个元素，记为a，计算POSP（D）和POSP-｛a｝（D），若相等则从集合P中去除元素a，消除属性集P中的冗余信息；

步骤6 算法结束，输出约简后的属性集P.

3 实例分析

表1为天气决策表［18］.表1中：a1，a2，a3，a4为条件属性，分别代表天气、温度、湿度、风；d是决策属性；论域U＝｛x1，x2，…，x14｝.此外，表1中括号中数字为对应的天气决策表的数字表示，如a1＝｛晴，多云，雨｝＝｛1，2，3｝；a2＝｛热，温暖，冷｝＝｛1，2，3｝，a3＝｛高，正常｝＝｛0，1｝；a4＝｛否，真｝＝｛0，1｝，d＝｛N，P｝＝｛0，1｝.

对此决策表运用文中的方法.

表1 天气决策表Tab.1 Weather decision table

考察ai（i＝1，2，3，4），在C中相对于D来说是否必要.为此，从C中去掉a1可得：POSC-｛a1｝（D）≠POSC（D），所以a1必要 .同理可得a2，a3不必要，a4必要，那么可得P1＝CORED（C）＝｛a1，a4｝，U／P＝｛｛1，8，9｝，｛2，11｝，｛3，13｝，｛3，5，10｝，｛6，14｝，｛7，12｝，不可分辨的集合为｛｛1，8，9｝，｛2，11｝｝.那么新的决策表为C＝｛a2，a3｝，U＝｛1，2，8，9，11｝，如表2所示 .

考察ai（i＝2，3），在C中相对于D来说是否必要.同理可得a2为不必要的，a3为必要的，那么可得P2＝CORED（C）＝｛a3｝，U／P2＝｛｛1，2，8｝，｛9，11｝｝，分辨完全.即可得P＝P1∪P2＝｛a1，a3，a4｝.则有

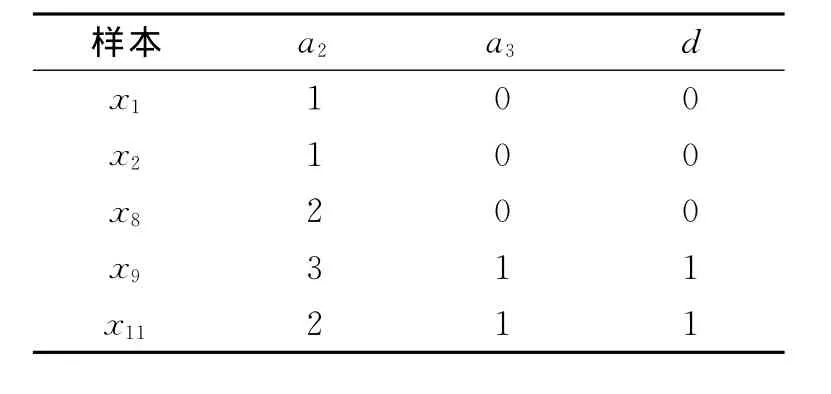
表2 新的决策表Tab.2 New decision table

由此可得POSP（D）≠POSP-｛a1｝，POSP（D）≠POSP-｛a3｝，POSP（D）≠POSP-｛a4｝.所以，约简集合为｛a1，a3，a4｝.采用 UCI数据库进行测试，结果如表3所示.

表3 试验结果Tab.3 Test results

4 结束语

粗糙集理论目前已日趋完善，被广泛用在许多领域上 .所提出的约简算法利用相对核对论域进行划分，从而求得属性约简，降低了时间和空间上的复杂度 .经测试，该方法能够得到合理的结果，为数据决策表的属性约简提供一条较为可行有效的途径.

［1］ 王国胤，姚一豫，于洪.粗糙集理论与应用研究综述［J］.计算机学，2009，32（7）：1229-1246.

［2］ PAWLAK Z.Rough set［J］.International Journal of Computer and Information Sciences，1982，11（5）：341-356.

［3］ CHAN C C，GRZYMALA-BUSSE J W，ZIARKO W P.Rough sets and current trends in computing［C］∥Proceedings of the 6th International Conference on RSCTC.Akron：［s.n.］，2008.

［4］ AN A，STEFANOWSKI J，RAMANNA S，et al.Rough sets，fuzzy sets，data mining and granular computing［C］∥Proceedings of the 11th International Conference on RSFDGrC.Toronto：［s.n.］，2007.

［5］ WANG G Y，LI T R，GRZYMALA-BUSSE J W，et al.Rough sets and knowledge technology［C］∥Third International Conference on Rough Sets and Knowledge Technology.Chengdu：［s.n.］，2008.

［6］ 曾小军，黄宜坚.利用AR模型和支持向量机的调速阀故障识别［J］.华侨大学学报：自然科学版，2011，32（1）：13-17.

［7］ 陈叶旺，于金山.一种改进的朴素贝叶斯文本分类方法［J］.华侨大学学报：自然科学版，2011，32（4）：401-404.

［8］ PAWLAK Z，GRZYMALA-BUSSE J，SLOWINSKI R，et al.Rough sets［J］.Communications of the ACM，1995，38（11）：89-95.

［9］ PAWLAK Z.Why rough sets［C］∥Proceedings of the Fifth IEEE International Conference on Fuzzy Systems.New Orleans：IEEE Press，1996：738-743.

［10］ WONG S K M，ZIARKO W.On optional decision rules in decision tables［J］.Bulletin of Polish Academy of Science，1985，33（11／12）：693-696.

［11］ HU Xiao-hua，GERCONE N.Learning in relational databases：A rough set approach［J］.International Journal of Computational Intelligence，1995，11（2）：323-338.

［12］ 叶东毅.Jelonek属性约简算法的一个改进［J］.电子学报，2000，28（12）：81-82.

［13］ 刘少辉，盛秋戬，史忠植.一种新的快速计算正区域的方法［J］.计算机研究与发展，2003，40（5）：637-642.

［14］ 刘少辉，盛秋戬，吴斌，等 .Rough集高效算法的研究［J］.计算机学报，2003，26（5）：524-529.

［15］ 胡峰，王国胤 .二维表快速排序的复杂度分析［J］.计算机学报，2007，30（6）：963-968.

［16］ 徐章艳，刘作鹏，杨炳儒，等.一个复杂度为 max（O（｜C｜｜U｜），O（｜C｜～2｜U／C｜））的快速属性约简算法［J］.计算机学报，2006，29（3）：391-399.

［17］ 王国胤，于洪，杨大春.基于条件信息熵的决策表约简［J］.计算机学报，2002，25（7）：759-766.

［18］ 瞿彬彬，卢炎生.基于粗糙集的属性约简算法研究［J］.华中科技大学学报：自然科学版，2005，33（8）：30-33.