基于统一设备架构的影像实时MTF补偿方法

孙业超 朱晓波 郝雪涛

(中国资源卫星应用中心，北京 100094)

1 引言

光学成像系统调制传递函数(Modulation Transfer Function，MTF)是表征光波经成像系统后在频率域中调制衰退的函数，是光学成像系统性能的一个重要评价指标。由于遥感图像的光学信息获取与传输过程要经过目标、大气、光学系统、CCD等一系列环节，各个环节均可能对图像产生退化作用，引起图像质量(Quality)的下降[1]。MTF值反映了成像在不同空间频率的衰减情况，即频率越高，信号衰减的越多，MTF值就越小，所以图像在采样数字化的过程中损失的主要是高频信息，它在图像上表现为影像的边缘、细节等的模糊。为了改善成像的清晰度和成像质量，需要在地面处理系统中对数据进行调制传递函数补偿(Modulation Transfer Function Compensation，MTFC)，恢复影像的高频信息，让影像的边缘更为清晰,细节更为丰富。

随着遥感对地观测技术的不断发展，影像空间分辨率和量化分辨率的提高，使得下传影像数据量不断增大，目前的MTFC处理研究都是以中央处理器为核心，对于高空间分辨率的卫星影像处理，由于计算量大造成运行速度慢、耗时长，成为地面系统实时处理的瓶颈。

GPU是新一代高性价比的计算技术，近年来发展迅速。图形处理器在并行数据运算上具有强大的运算功能以及相对较高的并行运算速度，具有单指令流多线程(Single Instruction Multiple Thread, SIMT)的并行处理特性[2]，在解决计算密集型问题时具有较高的性价比[3]。2006年11月，英伟达公司推出了计算统一设备架构(Compute Unified Device Architecture, CUDA)，这是一种新的并行编程模型和指令集架构的通用计算架构，能够利用英伟达 GPU的并行计算引擎解决复杂计算任务，目前已经在医学成像与分割、大气辐射传输计算、图像编码以及光纤通信等领域中得到应用，显著地提高了传统算法处理的效率[4]。本文基于 CUDA架构对MTFC算法进行并行化设计，并根据算法特征进行优化，提高了运算速度，减少了算法执行时间，满足地面处理系统准实时处理的要求。

2 M TFC技术现状

基于MTFC的图像复原是图像增强处理技术中的一种，图像复原前的遥感图像是经过成像链路退化和其间引入噪声污染的图像，图像复原的目的就是处理这种图像得到未被退化和污染的图像的最佳估计。在卫星地面处理系统中一般采用刀刃法进行MTF在轨测量，并基于MTF曲线进行复原，复原算法采用维纳滤波[5-7]，MTFC过程如图1所示，可以分为MTF曲线计算、MTF矩阵计算和图像复原3个主要步骤，图1中FFT和IFFT分别为傅里叶变换与傅里叶逆变换。

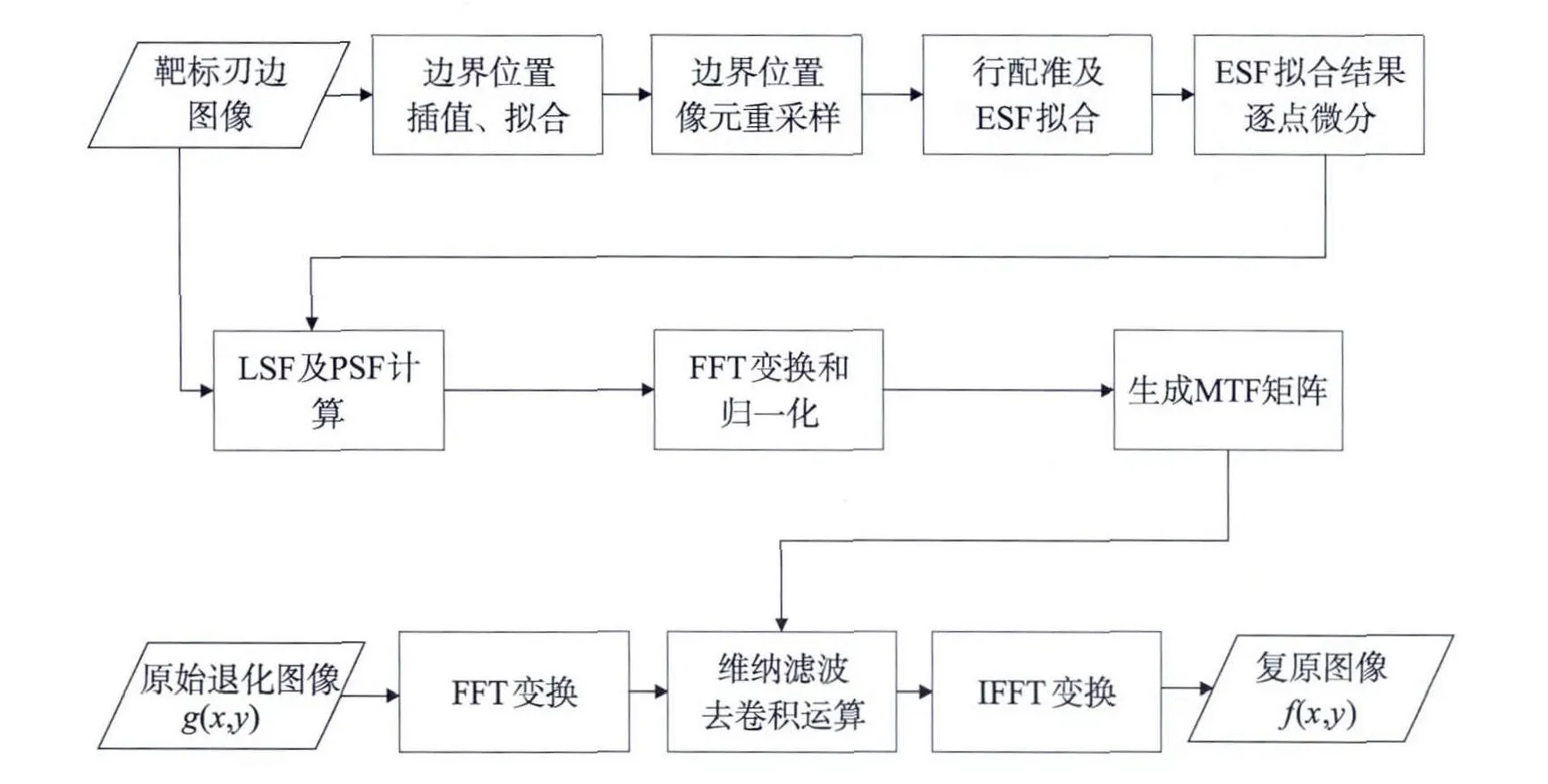
图1 地面处理系统中的MTFC流程Fig.1 The flow of MTFC

在不考虑噪声的情况下，刀刃法利用靶标或图像中低反射率目标和高反射率目标相交直线为参考，在直线实际亮度突变函数用f(x,y)表示，若相机的综合响应函数为h(x,y)，对于一个线性不变系统，则输出图像函数g(x,y)为[8]

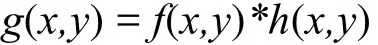
式中 * 为卷积运算符号；x,y为空间域像素坐标；f(x,y)为原始图像函数；g(x,y)为经过大气衰减、星载光学系统、传感器、电子线路后退化的图像函数；h(x,y)为综合所有退化因素的函数，即点扩散函数(Point Spread Function, PSF)。测量过程中，首先利用灰度进行边缘检测，检测出的边缘点并非严格位于一条直线上，需要对边界位置拟合、重采样，然后进行行配准得到边界位置的灰度分布，利用多项式拟合获得边界扩散函数(Edge Spread Function, ESF)，对ESF进行微分可以得到线扩散函数(Line Spread Function,LSF)。对LSF进行离散傅里叶变换，取变换之后各分量的模为各频率的MTF值，并以第1个MTF值为基准，作归一化处理，就得到了一系列MTF值。由于截止频率处的MTF值趋近于0，将频率点以截至频率为基准作归一化处理，则截止频率为1，取频率0～1处的MTF值构成光学系统的MTF曲线。

建立MTFC模型必须要构建二维的MTF矩阵。常规的处理方法是将水平MTF列向量乘以垂直MTF列向量，即：

式中 M TFu为在频率u处水平的MTF值；M TFv为在频率v处垂直的MTF值；M TF(u,v)为二维频率坐标为(u, v)处的MTF值。这种方法求得的45º方向的MTF值与水平或垂直方向的MTF值差别较大，为了消除这种差别，同时取水平与垂直方向0.5频率处MTF值的平均值再衰减90%作为45º方向0.5频率处的MTF值，再根据水平与垂直方向的MTF向量之间的比例关系进行插值，即可得到二维插值MTF矩阵。由于模的对称性，只需要求出 0～0.5频率处的 MTF值，根据对称性即可得到–0.5～0频率处的MTF值，0.5频率即截止频率的一半。

基于 MTFC的图像复原一般采用维纳(Wiener)滤波算法，维纳滤波复原是一种对噪声起抑制和减少作用的方法[9]。维纳滤波复原算法为

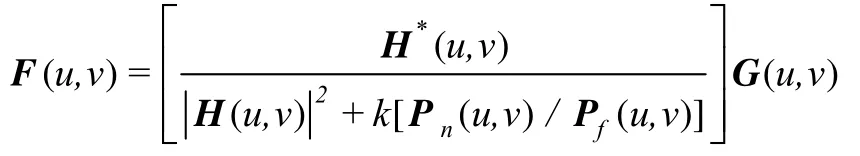
式中 F(u,v)为复原图像的频谱；G(u,v)为原始退化图像的频谱；Pf(u,v)和 Pn(u,v)分别为信号和噪声的功率谱密度；k为一个可调系统，一般为0.02；* 表示共轭，即

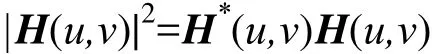
式中 H(u,v)为二维MTF矩阵。维纳滤波作为一种典型的有噪声约束下输入与估计最小均方误差(MSE)的复原方法，可以有效解决在高频处对噪声的放大。

3 基于CUDA的MTFC算法

3.1 CUDA技术

CUDA是一种将GPU作为数据并行计算设备的软硬件体系，其特点是将CPU作为主机，GPU作为协处理器或设备端，在这个模型中CPU和GPU协同工作，CPU负责逻辑性强的事务和串行计算任务，而GPU主要处理高度线程化的并行计算任务。在CUDA编程模型[10]中，如图2所示，运行在GPU上的CUDA并行计算函数称为Kernel，一个完整的CUDA程序是由一系列的设备端Kernel函数并行步骤和主机端的串行处理步骤共同组成，而Kernel是整个CUDA程序中的一个可并行执行步骤。在GPU端Kernel函数是以线程网络(Grid)的形式组织，每个Grid再由若干个线程块(Block)组成，每个Block中再包含很多个线程(Thread)。GPU线程的发起是轻量的, 其创建线程的系统开销非常小, 线程切换所耗费的时间也相当短。

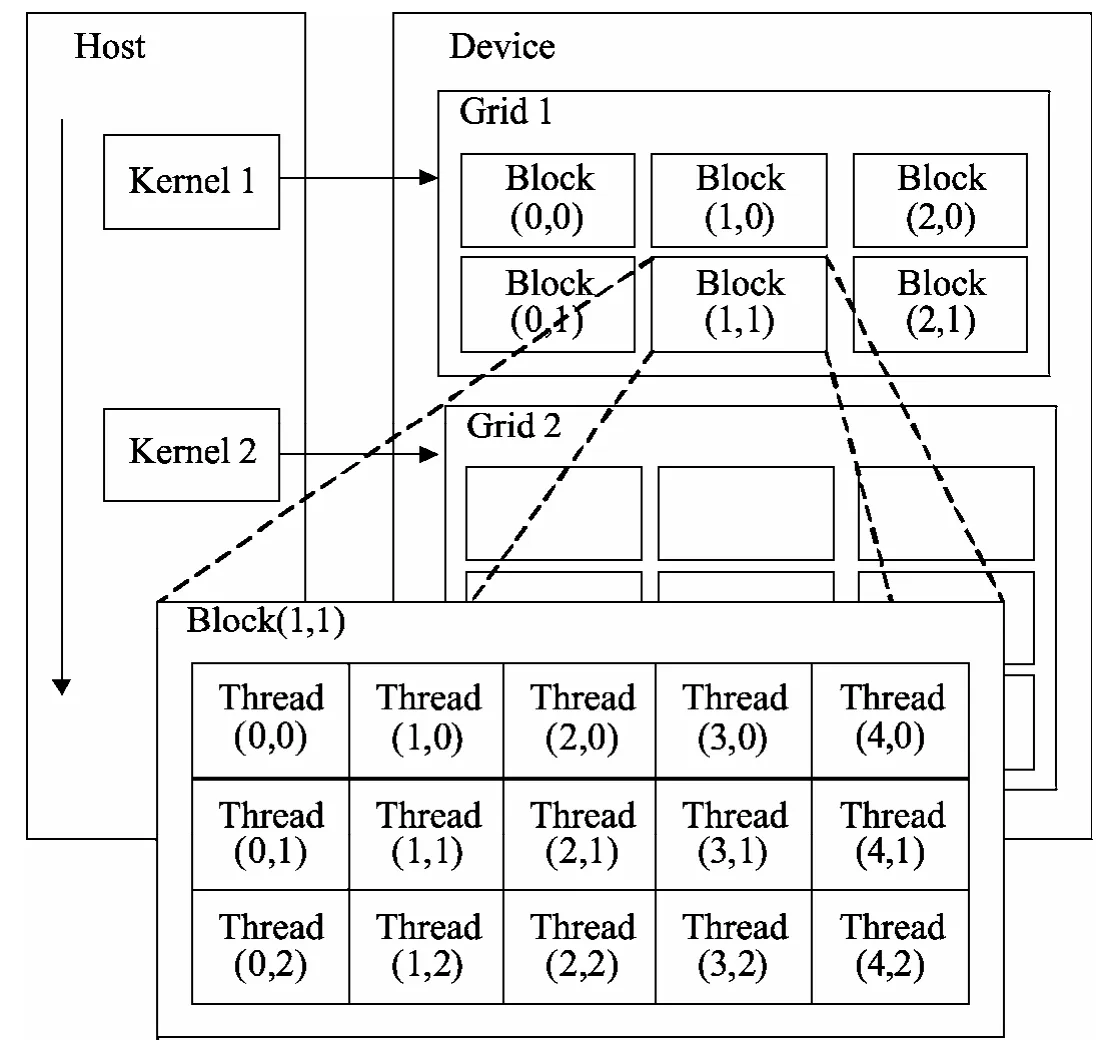
图2 CUDA编程模型Fig.2 CUDA programm ing model

3.2 MTFC方法并行设计

基于MTFC的复原要求每次处理的图像与二维MTF矩阵大小一致，而高分辨率、宽覆盖影像比较大，需要对图像进行分块处理。在地面系统处理中，为了消除维纳滤波的边缘影响，影像的四周边缘不进行复原处理，如图3(a)所示，对abcd为顶点的图像进行处理时，上下左右各8个像元的边缘保留原图像，所以直接对图像进行分块处理，会造成分块边界部分的复原质量下降，为了保证复原质量，本文设计了重叠分块的方法，如图3(b)所示，一个分块与左及上一个分块在行方向及列方向上都重叠16个像元，这样就能保证复原算法在分块边缘位置的连续，从而得到与传统算法一致的复原效果。

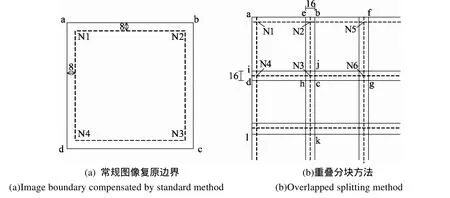
图3 图像并行分块方法Fig.3 Image splitting method for parallel computiong

按照线程块间并行和块内线程并行的结构，本文设计了MTFC复原的算法，图像复原的GPU算法流程如图4所示。GPU程序一般是通过Kernel函数来实现的，本文定义5个主要顺序执行的Kernel函数：1) Kernel 1 将图像量化类型转换为适合傅里叶变换的复合类型；2) Kernel 2进行傅里叶变换；3) Kernel 3 图像滤波复原；4) Kernel 4 进行傅里叶逆变换；5) Kernel 5 将复合类型转为图像量化类型。步骤中2)和4)采用CUDA中的CUFFT库来实现。

3.3 并行优化

直接将CPU程序在CUDA编程模型中进行重构，并不能带来性能的显著提升，只有对算法流程进行充分分析，根据算法特征进行设计和优化，才能高效地利用GPU的计算资源，获得数十倍乃至数百倍的加速比。基于CUDA实现并行算法，在数据分块、内核函数设计、存储器使用等方面都有较多的选择空间，因此基于CUDA实现并行算法可以有若干种实现方式，这样算法的加速比、高效存储器使用率、算法可以构成一个三维空间。性能优化的过程就是在三维空间逐渐寻找该最优点的过程。基于 CUDA实现的算法性能优化主要从以下三方面考虑：1)最大限度的GPU端并行执行；2)优化存储器使用以达到最大存储器访问带宽；3)优化指令流以获取最大指令吞吐量[10]。

共享存储器(Shared Memory)的合理使用可以提高线程的访存速度。共享存储器是GPU片内的高速存储器，它是可以被同一线程块中所有线程访问的可读写存储器[11]，一般而言可以在一到两个时钟内读写，因此使用共享存储器取代全局存储器会极大的节约带宽。本文通过分析MTFC算法，将二维MTF矩阵转化为一维矩阵，另外定义一个线程块一次处理的图像范围为一个逻辑块，将与该逻辑块对应大小的MTF值从GPU缓存拷入线程块的共享存储器，使得块内各线程通过共享的内存来实现完全循环解缠处理，提高了处理速度。

在CUDA编程模型中，必须要用足够多的活跃线程才能提高计算效能，隐藏访存延时[12]。因此线程块和逻辑块的大小，会影响 MTFC算法的执行效率，本文通过 CUDA效率分析器(CUDA Occupancy Calculator，COC)在GPU计算能力2.0的规格上进行分析发现，当线程块大小为256(即16×16)，且每个线程块使用的共享存储器数据量为8 192字节(即逻辑块大小为32×32)时，GPU线程束占用率达到最大值，如图5、6所示，这种情况下，GPU的计算资源和存储资源可以被完全使用。

图4 图像复原的GPU流程Fig.4 The flow of image restoration in GPU device

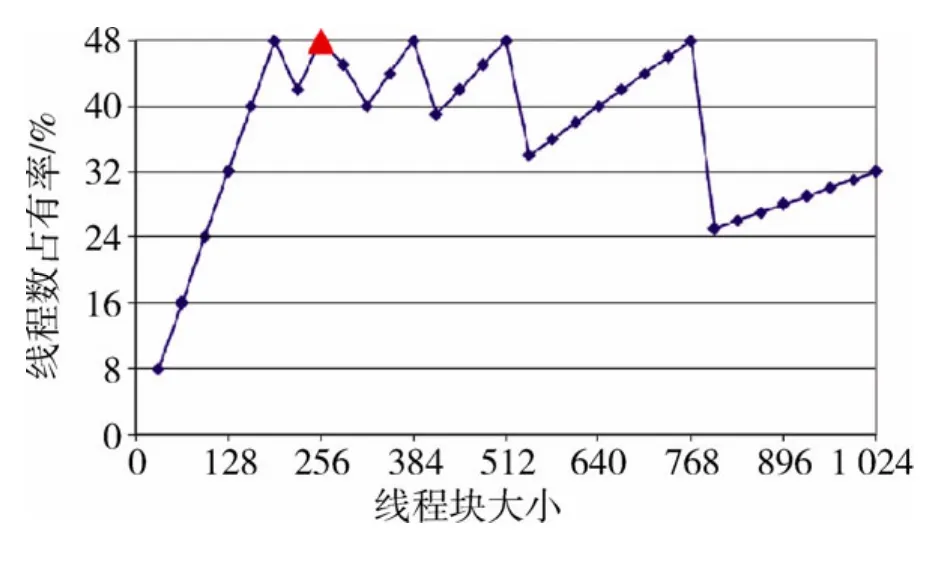
图5 线程块大小对效率的影响Fig.5 Impact of varying thread block size

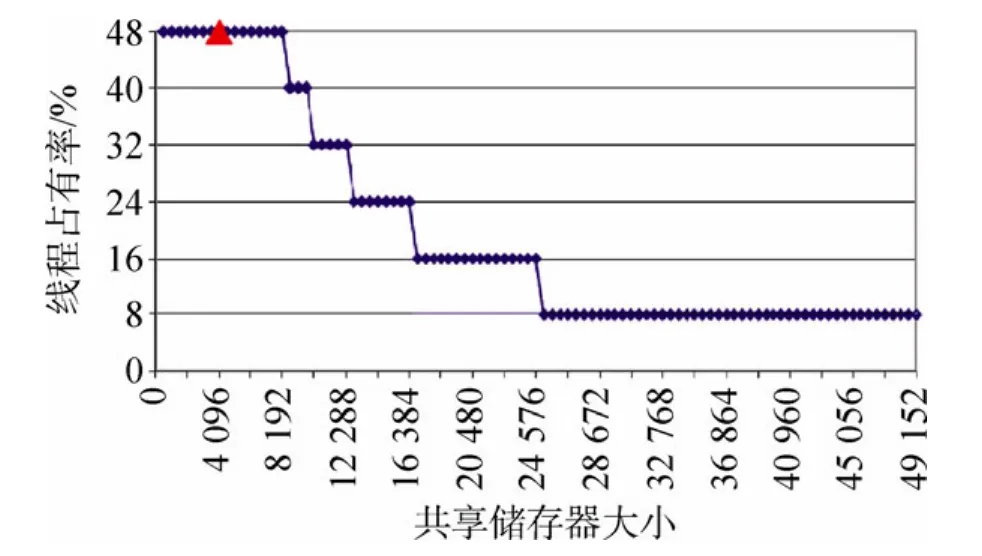
图6 共享存储器大小对效率的影响Fig.6 Impact of varying shared memory usage

4 实验结果与分析

为验证算法的有效性，本文设计、编写了基于CUDA的MTFC程序，并在硬件处理架构上进行实验。硬件平台为Intel Core 2 Duo i7处理器，8G内存，GPU平台为NVIDIA Quadro 2000M。操作系统为Windows 7，编译环境为M icrosoft Viusal Studio 2010、NVIDIA CUDA编译器NVCC。实验数据为资源三号卫星下视影像，图像大小为24 530×24 575像素，16 bit量化，数据量为1.2 GB。图7 为实验数据在CPU串行和GPU并行架构下进行MTFC处理的结果，由图中可以看出，经过复原处理，影像的边缘比原图更为清晰，细节更为丰富，通过图像软件比较，CPU串行MTFC处理及CUDA并行MTFC处理后的图像结果完全一致。

图7 待复原图像和复原结果Fig.7 Image restoration results base on CPU and CUDA

为验证算法在不同数据量情况下的计算效率上，本文分别从实验数据截取 6 000×6 000、12 000×12 000、18 000×18 000、24 000×24 000像元作为形成模拟图像，并对每个图像运行基于CUDA的MTFC程序和原CPU串行算法，连续运行5次记录运行时间(不计文件IO时间)的平均值，表1列出了基于CUDA的MTFC算法与原基于CPU的MTFC算法的执行时间和加速比。由表1中可以看出，基于CUDA的MTFC算法由于利用了GPU的众核计算资源，使得算法的执行时间大大缩短，图像复原步骤可以获得达到45倍的加速比，随着图像大小的增加，算法加速比逐渐增高，说明对于数据量越大的图像，GPU加速效果越明显，鉴于测试环境中GPU平台只是NVIDIA公司用于图形渲染的显卡，如果移植到用于科学计算的Tesla系列专业GPU卡上，将会有更大程度的速度提升。

表1 不同图像大小下的算法执行平均时间对比Tab.1 Comparison of average executing time

另外，在选择不同的线程块和逻辑块的大小时，MTFC算法的执行时间会有差别，图8列出了选择不同的线程块和逻辑块大小进行整景图像MTFC算法执行的时间。由图8可以看出，在线程块大小为16×16，逻辑块大小为32×32的情况下，算法执行时间最短，这与本文利用COC进行并行优化分析的结论是一致的。

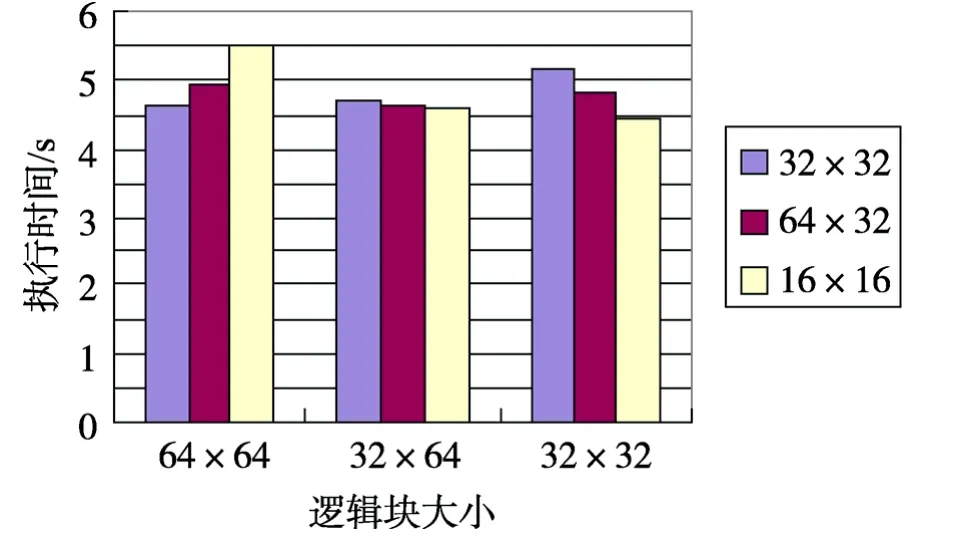
图8 不同线程块和逻辑块大小执行时间对比Fig.8 Varing logical block size and thread block size

5 结束语

本文提出基于CUDA架构的并行MTFC算法，通过分析MTFC算法流程及特征，采用线程块间及块内线程间两层并行模型，提高算法的并行度，另外，根据维纳滤波复原算法的特点对存储层次进行优化，提高共享存储器的使用率。实验表明，该算法与原CPU串行算法处理结果质量一致，但加速显著，在NVIDIA一般显卡环境下，即可达到45倍的加速比，大幅度提高了MTFC处理效率，如果移植到用于科学计算的Tesla系列专业GPU卡上，将会有更大程度的速度提升，在高分辨率卫星地面处理系统中具有很好的应用价值。

References)

[1]杨贵军, 邢著荣. 小卫星CCD相机MTF在轨测量与图像复原[J].中国矿业大学学报, 2011, 5(3): 481-486.YANG Guijun, XING Zhurong.On-orbit MTF Estimation and Restoration for CCD Cameras of Environment and Disaster Reduction Small Satellites(HJ1A/1B)[J]. Journal of China University of M ining & Technology, 2011, 5(3): 481-486. (in Chinese)

[2]Elsen E, Houstron M, Vishal V, et al. BN-body Simulation on GPUs[C]//Processing of 2006 ACM/IEEE Conference on Supercomputing, USA: New York, 2006: 188.

[3]Nvidia. CUDA Programm ing Guide Version 2.3.1[EB/OL]. http://developer.download.nvidia.com/compute/cuda/2_3/toolkit/docs/NVIDIA_CUDA_Programming_Guide_2.3.pdf, 2010-03-05.

[4]何国经, 刘德连.CUDA架构下高光谱图像光谱匹配的快速实现[J]. 航空兵器, 2011, 8(4): 3-6,12.HE Guojing,LIU Delian. High Speed Spectral Matching Approach for Hyperspectral Image Based on CUDA[J]. AERO WEAPONRY, 2011, 8(4): 3-6,12. (in Chinese)

[5]王先华, 乔延利, 易维宁.卫星光学相机MTF在轨检测方法研究[J]. 遥感学报, 2007,11(3): 318-322.WANG Xianhua, QIAO Yanli, YI Weining. In-flight Measurement of Satellite Optical Camera MTF[J]. Journal of Remote Sensing, 2007,11(3): 318-322. (in Chinese)

[6]顾行发, 李小英, 闵祥军, 等. CBERS-02卫星CCD相机MTF在轨测量及图像MTF补偿[J]. 中国科学, 2005, 35(1): 26-39.GU Xingfa, LI Xiaoying, M IN Xiangjun, et al. In-flight MTF Measurement and MTFC of CBERS-02 Satellite CCD Images[J]. Science in China, 2005, 35(1): 26-39. (in Chinese)

[7]吴昀昭, 宫鹏. 北京一号小卫星MTF 在轨测量与图像复原[J]. 遥感应用, 2007, (3): 49-53.WU Yunzhao, GONG Peng. On-orbit MTF Estimation and Restoration of Beijing-1 Images[J].Remote Sensing Application,2007, (3): 49-53. (in Chinese)

[8]周春平, 宫辉力, 李小娟, 等. 遥感图像MTF复原国内研究现状[J]. 航天返回与遥感, 2009, 30(1): 27-32.ZHOU Chunping, GONG Huili, LI Xiaojuan, et al. The Summary of MTF Restoration on Remote Sensing Image[J].Spacecraft Recovery & Remote Sensing, 2009, 30(1): 27-32. (in Chinese)

[9]Kundur D, Hatzinakos D. Blind Image Deconvolution[J]. IEEE Signal Processing Magazine, 1996, 13(3): 43-64.

[10]胡娅. 基于GPU的BLAST程序的并行计算的研究[D]. 杭州: 浙江理工大学, 2011.HU Ya. Research on GPU-based Parallel Computing on BLAST Program[D]. Hangzhou: Zhejiang Sci-Tech University, 2011.(in Chinese)

[11]张舒, 褚艳利. GPU高性能运算之CUDA[M]. 北京: 中国水利水电出版社, 2009: 46.ZHANG Shu, ZHU Yanli. GPU High Performance Computing –CUDA[M]. Beijing:China Water Power Press, 2009: 46. (in Chinese)

[12]Muthu M B, Rajesh B. Optim izing Sparse Matrix-vector Multipli-cation on GPUs[R]. [S.1.]: IBM, 2008.