一种解决黑洞奇点的方案

王晓明

（山西大同大学物理与电子科学学院，山西大同037009）

一种解决黑洞奇点的方案

王晓明

（山西大同大学物理与电子科学学院，山西大同037009）

该文提出一种解决黑洞奇点的方案，即引力相互作用的高能截止方案。根据这个方案可以得出一些重要的结论，例如时空量子化、测不准关系的修改等。

黑洞奇点；截断；测不准关系

黑洞奇点问题是当今理论物理学中急需解决的问题。 这个问题的解决对理论物理学和天文学的发展都有重要的意义。为此，本文提出一种解决方案。

1 黑洞奇点问题简介

1915年，爱因斯坦提出了广义相对论，不久德国科学家Schwarzschild利用广义相对论求出了球对称物体周围空间的度规：

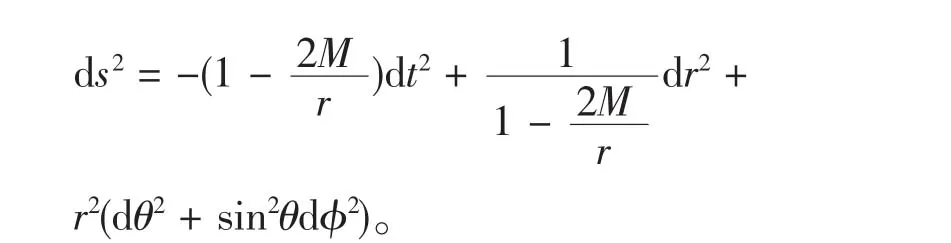
从这个度规里可看到两个奇点，即r=2M和r=0。后来经过研究，人们发现，r=2M点只是坐标奇点，不是真正的奇点，而r=0才是真正的奇点，在这点时空曲率发散。

1939年，美国物理学家J.R.Oppenheimer和H. Snyder提出，超过3倍太阳质量的恒星在演化晚期将坍塌成黑洞，黑洞中心有一个奇点，在这点上密度和曲率为无穷大。上世纪60年代英国物理学家罗杰·彭罗斯和斯蒂芬·霍金根据广义相对论并且利用整体微分几何的方法，证明了在黑洞中必然存在无限大密度和时空曲率的奇点[1-4]。黑洞奇点问题是当今理论物理学和天文学中一个最令人头疼的问题，因为在奇点密度和曲率无穷大，在物理学中无穷大是没有意义的，因为自然界中发生的过程和结果必须是有限的，无穷大的现象说明我们的理论已经不适用了。为了解决黑洞奇点问题，彭罗斯提出了宇宙监督方案[5]，即黑洞奇点被包围在视界之内，人们无法看到奇点，黑洞奇点不会影响黑洞外的世界。但这个方案，一方面其实并没有真正解决黑洞奇点问题，即黑洞奇点并没有去掉，无穷大密度依然存在。另一方面有时在一定条件下，最普遍的黑洞，即克尔-纽曼黑洞会出现裸奇点[1-3]，奇点外面没有视界，裸奇点能影响我们的世界，破坏因果性。这就说明宇宙监督方案不是一个彻底解决黑洞奇点的理论。随着量子力学和量子场论的发展，人们逐渐认识到广义相对论和现代微分几何其实只能算是经典理论，它们没有考虑量子效应，在奇点附近引力将变得异常强大，量子效应必须考虑，而且量子效应应该占主导地位。所以黑洞奇点问题必须用量子引力理论来解决。早期的量子引力理论存在着无穷大问题，而且不能重正化。人们也尝试建立了各种量子引力理论，例如超弦理论[6-7]、圈量子引力[8-9]、CausalDynamical Triangulation理论[10-11]、Massive Gravity理论[12]等等，但这些理论都存在某些缺陷和无法解决的问题，还不能被认为真正的量子引力理论，而且这些理论也没有提出一个真正解决黑洞奇点的方案。所以到目前为止，黑洞奇点问题还一直没有得到彻底解决，就象漂在物理学上空的一朵“ 乌云”。

2 黑洞奇点问题的一个解决方案

现在知道，处理微观物体间相互作用问题必须用规范场论，量子引力理论也必然属于规范场论。规范场论认为，微观粒子之间的相互作用是通过中间玻色子来传递的。通常用规范场论计算相互作用的振幅时都要碰到积分无穷大的问题，主要是由于积分时动量或能量的积分上限为无穷大，所以导致积分发散。在实践中人们用重正化的方法，也就是定义无穷大的裸的电荷、质量、波函数等和有限的物理电荷、物理质量、波函数，来消除无穷大。这种方法在电磁、强、弱相互作用中取得了极好的效果，计算结果与实验数据非常吻合。但运用到引力时遇到了麻烦，需要引入无数的重正化量，使得重正化方法在量子引力中无法实现。然经过无数物理学家的长期不懈地努力，但仍然无法解决量子引力无穷大问题，因此与引力相关的许多问题无法得到解决，黑洞奇点问题就是其中最典型的代表。要解决黑洞奇点问题关键是使得量子引力计算中积分收敛，要达到这个目的，笔者觉得有两种方法，一种是保持积分上限无穷大，找到可行的重正化方法；另一种是使得积分上限为有限，这样自然积分收敛了。但积分上限并不是人为规定的，而应该由理论本身决定的。现在分析一下积分上限应该为多少？我们知道，中间玻色子也是一种微观粒子，由量子力学可知，任何微观粒子都具有波粒二象性，而且遵守测不准关系，这是量子力学与经典力学的最本质的区别。测不准关系的内容是粒子的坐标和动量不能同时确定，坐标的不确定量和动量的不确定量满足一个不等式，即

△x△p≥ ħ/2。

还有时间和能量也不能同时确定，时间不确定量和能量不确定量也满足关系：

△t△E≥ ħ/2。

根据测不准关系，当粒子坐标越精确，也就是活动范围越小时，动量不确定性就越大，特别地，当△x→0时，△p→∞。粗看好像没什么问题，但我们细想一下这个结果就不太符合道理。我们知道，振动是需要时间和空间的，△x→0，也就是在一个点上振动是没有意义的，振动必须有一定空间范围，如果这个范围太小了，无限趋近于零，粒子将无法振动，那么，这时动量的不确定量将趋于零，如果是这样的话测不准关系将不成立，同样如果时间间隔太短，粒子也无法振动，也就是说当△t→ 0时，△E→0。笔者觉得虽然这个结论与现有理论不一致，但符合逻辑推理，应该是正确的。如果这个结论正确的话，粒子振动的波长有一个下限，即 必须大于某一个值，这说明粒子振动的频率有一个上限，这表明粒子的动量和能量有一个上限，也就是说粒子的动量和能量不能是无穷大。那么当粒子距离黑洞奇点到一定距离时，传播引力的中间玻色子（也可以说引力子）虽然是虚粒子，但它也要振动，因为粒子与黑洞奇点距离太近，所以中间玻色子振动频率无法再增加，因此动量和能量的最大值就不能是无穷大，有一个上限，因此积分就收敛了，引力也就不趋于无穷大了。这样，也许就能克服黑洞奇点了，这就是笔者的方案的主要内容。当然这只是一个主观的想法而已，没有经过严格的证明，今后应该用严格地推导来证明这个想法。

3 讨论

1）上面想法应该有一些普遍性，似乎能够应用到其它相互作用，但目前其它三种相互作用可以用重正化理论解决，不知这种想法与重正化理论是否吻合，这将是以后的重要工作。

2）由这个想法似乎可以得到这样一个结果：时空似乎是量子化的，即时间和空间间隔似乎有一个最小值，当时间和空间小于这个值时，测不准原理不再适用，粒子将不振动，一些物理原理可能将不再适用。当然时空的最小量子到底是多少，在这样的范围内有什么样的全新的规律，还需要以后进一步研究。

[1]Misner CW，Thorne K S，Wheeler JA.Gravitation[M].San Francisco：Freeman，1973.

[2]Wald R M.General relativity[M].Chicago and London：The University of Chicago Press，1984.

[3]Hawking SW，Eills G FR.The large scale structure of space-time[M].Cambridge：Cambridge University Press，1973.

[4]（英）霍金S，彭罗斯R.时空本性[M].杜欣欣，吴忠超译.长沙：湖南科学技术出版社，1996.

[5]梁灿彬.微分几何入门与广义相对论[M].第2版.北京：科学出版社，2006.

[6]Michael BGreen，John H.Schwarz dward Witten，Superstring Theory（Ⅰ，Ⅱ）[M].Cambridge：Cambridge University Press，1987.

[7]Joseph Polchinski.String theory（Ⅰ，Ⅱ）[M].Cambridge：Cambridge University Press，1998.

[8]Ashtekar A，Lewandowski J.Background IndependentQuantum Gravity：A Status Report[J].Class Quantum Gravity，2004，R53：21.

[9]Thiemann T.Introduction to Modern Canonical Quantum General Relativity[M].Cambridge：Cambridge University Press，200.

[10]Ambj¢rn J，Jurkiewicz J，Loll R.A non-perturbative lorentzian path integral for gravity[J].Phys Rev Lett，2000，85：924.

[11]Ambj¢rn J，Jurkiewicz J，Loll R.Reconstructing the universe[J].Phys Rev D，2005，72：064014.

[12]Bergshoeff E A，Hohm O，Townsand PK.Massive gravity in three dimentions[J].Phys Rev Lett，2009，102：201301.

A Resolving Project of Black Hole Singularity

WANG Xiao-ming
（School of Physics and Electronics Science，ShanxiDatong University，Datong Shanxi，037009）

This paper puts forward a resolving projectof black hole singularity，namely the high energe truncation of gravitational interaction.According to this project，some important results can be obtained，for example，spacetime quantization and modification of uncertainty principle.

black hole singularity；truncation；uncertainty principle. 〔责任编辑 李海〕

O412.3

A

1674－0874（2013）06－0019－03

2013-08-15

山西大同大学博士科研启动资金[2008-B-10]

王晓明（1967-），男，山西长治人，博士，讲师，研究方向：宇宙学。