全排列顺序解的非递归算法
白宇
(山西大同大学数学与计算机科学学院,山西大同037009)
全排列顺序解的非递归算法
白宇
(山西大同大学数学与计算机科学学院,山西大同037009)
通过对数字递增排序进行分析,提出了一种可以按序求解全排列的非递归算法,并进行了数学分析.该算法比传统的递归算法有更高的效率和更低的空间复杂度,可以简化一些穷举问题的求解过程.
全排列;递增排序;顺序解;穷举问题
在计算机算法设计中,有一类问题属于NP问题,只能通过穷举算法求解[1-3],例如哈密尔顿路径问题;或者虽不属于NP问题,但利用穷举算法求解更为方便,例如N皇后问题、约瑟夫环问题等[1-2]。在此类问题中,有一些类型,其求解等价于全排列问题的求解[1-3],例如N皇后问题.通过全排列求解可以简化原问题,由于全排列的时间复杂度为O(n!),当问题规模较小时,具有实用价值。
传统求解全排列的算法有两种:一是通过逐一交换每个位置的不同元素;二是在附加空间中逐一增加源序列中不同位置的每个元素[4-5]。这两种算法均为递归算法,需消耗较大的递归栈空间和辅助空间。从数字递增排序的角度出发,提出了一种非递归求解全排列的算法,其效率较高,无需递归栈空间,且可求得全排列的顺序解。
1 算法设计
求解全排列有两种思路:一是直接对元素进行排列;二是对位置进行排列,然后转换为元素[6]。由于待排列的元素可以是各种类型,可能不便对其进行运算或比较大小,因此第二种思路适应性更强,本文所述算法即基于第二种思路设计。
设源序列e中各元素的位置从左到右依次为:

根据全排列的定义,则对e的全排列求解便转换为对数字1到n可构成的所有数字递增排序的求解。由于该n个数字均不相等,因此,其构成的全排列可由小到大表示为n!个数字。
显然,(1)式所构成的数字可表示为:

此时,(2)式是所有可构成的数字中最小的,将(2)式的数字翻转,得:

此时,(3)式是所有可构成的数字中最大的。对序列e求全排列顺序解的过程,即是求从(2)式到(3)式的数字递增排序的过程。
将(1)式表示为p:
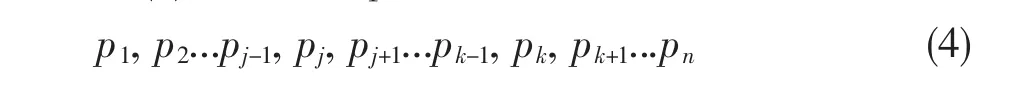
从(4)式的排列开始可由4个步骤找到大于(4)式的最小排列,即下一个排列:
step1从排列的尾部(最右边)开始,找出第一个比右边相邻数字小的索引j(j从首部开始计算),即j=max{i|pi<pi+1};
step2在pj右边的数字中,找出所有比pj大的数字中最小的数字的索引k,即 k=max{i|pi>pj};由于pj右边的数字是从右至左递增的,因此k是所有大于pj的数字中索引最大的;
step3交换pj与pk;
step4将pj+1...pk-1,pj,pk+1...pn翻转得到 p的下一个排列p′:
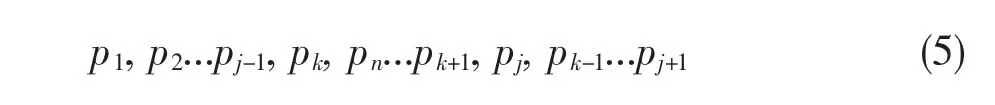
所述算法通过不断重复上述过程,直到在step1中查找j失败,此时已经得到了(3)式所表示的最大排列。
上述步骤的正确性证明如下:
定理1 数字p逐位表示如(4)式,其中pj+1>…>pk-1>pk>pk+1>…>pn且 pj<pj+1,pk>pj,且 pk+1<pj,p′表示如(5)式,则p′为大于p的最小整数。
证明首先证明p′>p,利用反证法。
设p′≤p,有(5)式≤(4)式,则pk≤pj,与命题相悖,故p′>p;
其次证明p′为大于p的最小整数,同样利用反证法。
设∃p″,p″<p′且p″>p,则∃m,使得pm<pk且pm>pj,同时:

因为 pm<pk,且 pj+1>…>pk-1>pk>pk+1>…>pn且 pj<pj+1,根据关系的传递性得:
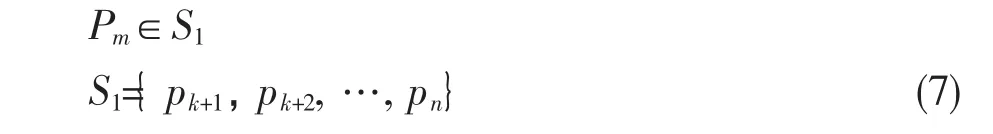
又因为pm>pj,且pk>pj,pk+1<pj,根据关系的传递性,有pm>pk+1,根据(6)式得:

由(7)式和(8)式得:

(9)式与假设相悖,即无法找到pm,因此pm不存在,故p′为大于p的最小整数,证毕。
例1 24310是位置编号0~4的一个排列,求它下一个排列。
解step1从右至左找出排列中第一个比右边相邻数字小的数字2,即j=1,pj=2;
step2在该数字后的数字中找出比2大的数中最小的数字3,即k=3,pk=3;
step3将2与3交换得到34210;
step4将原来2(当前3)后面的所有数字翻转,即翻转4210,得30124。
求得24310的下一个排列为30124。
2 算法分析
2.1 时间复杂度
首先,需构建元素位置的索引数组。
设每个元素的操作次数为1,则:

其次,step1所描述的查找pj的过程。由于子序列pj,pj+1...pk-1,pk,pk+1...pn的长度未知,不能采用二分查找算法[2-3],故采用顺序查找算法,其最坏情况时,操作次数与(10)式相同,即为n。
再次,step2所描述的查找pk的过程,同样采用顺序查找,其操作次数与(10)式相同,即为n。
最后,step4所描述的翻转 pj+1...pk-1,pj,pk+1...pn的过程,采用由序列两端向中间逐个交换元素的办法,因为每次交换涉及3次赋值操作,则:

已知n个数的全排列个数为n![1-3],所以,根据(10)式和(11)式,可知算法时间复杂度为:

2.2 空间复杂度
根据“算法设计”中的描述,本文所述算法的辅助空间分为两类。其一,表示元素位置的整型数据空间,其长度为n;其二,用于交换位置数据的辅助空间,其长度为1。因此,算法的空间复杂度为O(n).相对递归算法而言,空间复杂度由O(n!)降为O(n),且每个空间仅为32Bit的整形数据(由于元素数量较少可使用无符号byte类型,即最大表示28=256个元素位置)。
3 算法描述
1)sort(index),根据定理1,转换位置数组index
到下一个排列,如果成功则返回true,否则返回
false。其中index数组的长度为length。
1.length-2→j
2.if j<0 or index[j]≤index[j+1]then go 5
3.j-1→j
4.go 2
5.if j<0 then return flase
6.length-1→k
7.if index[k]≥index[j]then go 10
8.k-1→k
9.go 7
10.index[j]↔index[k]
11.j+1→j
12.length-1→k
13.if j≥k then go 18
14.index[j]↔index[k]
15.j+1→j
16.k-1→k
17.go 13
18.return true
2)perm(arr),对任意类型的数组arr进行全排列。其中数组arr、index和result的长度相等,均为length。
1.0→i
2.if i≥length then go 6
3.i→index[i]
4.i+1→i
5.go 2
6.0→i
7.if i≥length then go 11
8.arr[index[i]]→result[i]
9.i+1→i
10.go 7
11.output result
12.if sort(index)then go 6
4 算法实现
使用JavaScript(ECMAScript)实现,本文仅给出sort和perm算法主体部分的实现,其余部分不再赘述。
function sort(index){
for(var j=index.length-2;j>=0&&index[j]>index[j+1];j--){}
if(j<0)return false;

5 结语
所述算法采用非递归设计,不需要保护和恢复现场,其效率较递归算法要高;由于无需递归栈空间,其空间复杂度较递归算法要低;并且能顺序求解全排列,在穷举算法中便于量化分析穷举过程。综上所述,该算法在求解一些穷举问题时具有实用价值,可替代传统全排列的递归求解算法。
[1]Robert Sedgewick,Kevin Wayne.Algorithms Fourth Edi-tion[M].New Jersey:Pearson Education,2012:101-181.
[2]Torben Hagerup.Algorithm Theory-Swat2004[M].New York:Springer Verlag,2004:99-155.
[3]Bergin,Joseph.Data Structure Programming[M].New York:Springer Verlag,2005:78-105.
[4]Cormen,Thomas H.(EDT)/Leiserson,Charles E./Rivest,etal.Introduction To Algorithms[M].Massachusetts:Mit Pr,2005:166-192.
[5]Donald Knuth.The Artof Computer Programming,Volume 4[M].US:Addison-Wesley,2005:62-76.
[6]Miklos Bona.Combinatorics of Permutations[M].UK:Chapman Hall-CRC,2004:125-137.
Non-recursive A lgorithm of F ull P ermutation O rdinal S olution
BAIYu
(School of Mathematics&Computer Science,ShanxiDatong University,Datong Shanxi,037009)
Analyzed by ascending sort of digital,this paper designed non-recursive algorithm of ordinal solving the full permutation,and itsmathematical analysis.The algorithm has higher efficiency and lower space complexity than conventional recursive algorithms,it can simplify the solution procedure for exhaustive problem.
full permutation;ascending sort;ordinal solution;exhaustive problem 〔责任编辑 高海〕
TP312.12
A
1674-0874(2013)06-0009-03
2013-08-08
白宇(1976-),男,山西大同人,硕士,讲师,研究方向:图论算法,并行算法,云计算。

