基于贝叶斯公式的新生产线引进随机决策分析

武俊兰

（忻州师范学院，山西忻州034000）

基于贝叶斯公式的新生产线引进随机决策分析

武俊兰

（忻州师范学院，山西忻州034000）

企业的生产经营活动中随时随地都存在着随机性决策。随机性决策是否合理取决于决策信息是否被有效的利用。贝叶斯公式可以将模型信息、数据信息、先验信息等有效的结合起来，帮助企业管理者获得最优的决策方案。论文介绍了贝叶斯决策模型和相关概念，结合具体实例说明了贝叶斯随机决策的操作应用，对企业的随机决策管理具有一定的指导意义。

贝叶斯公式；随机决策；信息

1 相关概念

1.1 决策的定义

决策指的是决策者对以前和现在的各种相关信息进行研究之后，对未来或者现在可能出现的不利情况进行预测和判断，并在各种可行性方案中选择最佳方案的过程。正确的决策可以增加企业的收益，减少企业的损失，所以决策者必须掌握合理的决策方法，避免不必要的损失。决策环境受到多方面因素的影响，具有很大的不确定性，所以它带有一定的随机性。通常，决策者可以利用的有效信息越多，其作出正确决策的可能性就越大，决策的风险也就越小。

1.2 随机决策三要素

通常，随机决策问题主要由三个因素构成：一是自然状态因素，即各种自然状态构成的状态集；二是决策者行动因素，即决策者所有行动构成的行动集；三是决策者行动后果因素，即决策者采取某种行动之后可能造成的各种后果所构成的行为后果集，通常以收益或者经济损失函数来表示。

1.3 先验概率与后验概率

在实际中，决策者受社会环境和自然环境的影响，会积累很多经验，这些经验被称为先验信息。虽然先验信息不能对未来可能出现的情况作出具体的判断，但是很多情况下，这些先验信息都可以状态集上给出一个先验分布，决策者可以根据这一状态集对未来可能出现的概率作出估算。此时先验信息是可用的，决策者可以根据先验概率状态和期望值准则选择出最优的决策方案。

先验概率虽然在某些条件下可以作为决策者选择决策的依据，但是它通常具有很强的主观意见，受个人影响较大，所以不能真实的反映客观事实。要减弱先验信息的主观性就需要引入新的信息，获取新的数据，对先验概率进行修正，也就是常说的后验概率。

后验概率的以贝叶斯公式为基础进行计算的，所以又被称为贝叶斯决策模型。

1.4 随机决策原则

随机决策中常用的原则主要有以下几种：

一是期望值原则。顾名思义，就是计算不同自然状态下不同决策方案的损益期望，并以此为依据确定最优决策方案。通常是以收益最大或损失最小的方案为最优。这种方法的不足之处是，不同自然状态下的概率都是以以前的统计资料或者是以往的经验为基础的，具有一定的随机性和主观性，不能完全反应客观现实，所以估算结构可能与实际结果不相符。

二是最小方差原则。最小方差原则主要是对方案损益值进行控制，使其尽可能的集中在期望值附近。若方案的实际损益值和期望值之间的偏差越小，说明决策风险越小，反之则风险越大。

三是最小随机系数原则。期望值会对离散程度带了一定的影响，为了避免这种影响，通常用随机系数来判断随机的大小，增强不同方案之间的可比性。随机系数 =不同方案的标注差/其损益期望值，比值越大，决策风险越大，反之亦然。决策随机系数也可以通过信息熵测度法，贝叶斯随机法测量。

四是满意原则。首先确定一个目标值，然后把不同决策方案不同自然状态下的损益值和确定的目标值进行对比，损益值等于或者优于目标值的最大概率方案就是最有方案。

常见的随机决策方法还有效用期望值分析法、决策树法、现金流量分析法等。在具体操作时，决策者往往将几种方法同时运用，通过信息价值分析，加强随机决策可靠性。

2 贝叶斯公式

贝叶斯公式用事件形式表达如下：

假设X为随机试验Y的样本空间，A1，A2，…，

其中：P（Ai）表示的是事件Ai发生的概率，P（Bi）表示事件Bi发生的概率， P（B｜Ai）表示的是在事件Ai出现的概率下，事件B出现的概率。

决策者在进行决策时，其方案的选择往往取决于某些自然状态，但是这种自然状态却是未知的。通过大量的实验研究和事实调查发现，未知的某种自然状态实际是可以获得的。比如企业在决策是否采用新的生产工艺线时，决策的关键点在于新产品是否处于畅销状态。而产品的市场销售状态是可以通过调查获得的。所以，此时决策者就可以通过贝叶斯公式对新生产工艺是否可以投产作出判断。

3 实证分析

案例：某企业经营食品生产多年，经过公司高层管理人员的考察，目前打算从国外引入一批新的生产工艺，将企业产品进行全面升级。现在是否引入新生产工艺上面临两种选择：一种是继续保持原有工艺，一种是采用新工艺。新工艺产品的销量是决定企业选择哪种工艺的关键，因此，新工艺产品的销售状况是企业是决定否选择新工艺的关键。

厂长根据个人经验感觉新生产线的产品比原有产品好卖，认为新工艺决策（C1）的可能性P（C1）=0.6，旧工艺生产系统的决策性（C2）的可能性P（C2）=0.4。但考虑到新工艺引进费用较大，关系到企业未来的发展，厂长的先验决策个人主观意识较强，缺乏科学性和合理性。所以，经过慎重考虑之后，厂长决定先引入部分新工艺系统，使新工艺和原有工艺共同生产、销售。对两种产品的实际销售情况进行市场调研后再来决定是否全部更换。

新旧两种工艺系统产品实际销售情况概率P（Xn｜Ci），如表1所示。

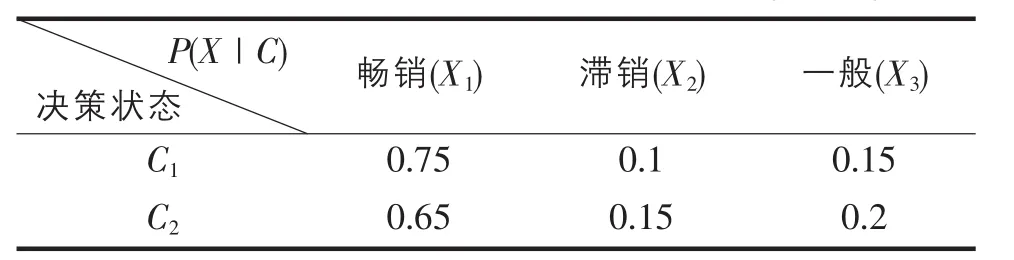
表1 不同决策情况下的销售概率分布P（Xn｜Ci）

由上述公式可知：

P（X1）=P（X1C1）+P（X1C2）=P（C1）P（X1｜C1）+

P（C2）P（X1｜C2）=0.65*0.75+

0.35*0.65=0.4875+0.2275=0.715；

P（X2）=P（X2C1）+P（X2C2）=P（C1）P（X2｜C1）+

P（C2）P（X2｜C2）=0.65*0.1+

0.35*0.15=0.065+0.0525=0.1175；

P（X3=P（X3C1）+P（X3C2）=P（C1）P（X3｜C1）+

P（C2）P（X3｜C2）=0.65*0.15+

0.35*0.2=0.0975+0.07=0.1675。

用贝叶斯公式对其进行修正即可获得后验概率P（Cn｜Xi），具体如表2所示

表2 不同决策情况下的销售概率分布P（Cn｜Xi）

假设各销售状态下的盈利情况如表3所示

表3 两种决策的盈利表

所以，两种决策下的平均盈利值为：

E（C1）=0.68*12.3+0.55*（-1.7）+0.58*4.6=

8.364-0.935+2.668=10.097

E（C2）=0.32*11.5+0.45*（-1.3）+0.42*4.2=

5.175-0.585+1.764=6.354

明显E（C1）＞E（C2），新的生产工艺未来给企业带来的收益更高，企业所承受的风险更小，所以企业应选择新生产工艺决策，对产品生产工艺进行升级。

一方面决策者的先验概率并不是完全不可信的，另一方面调查分析的结果也不是完全可靠的。贝叶斯分析法将两者结合在一起，既考虑到决策者的先验概率，又充分利用调查结果对其进行必要的修正，所以得到的结论相对来说也更加可靠，因此说贝叶斯模型大大降低了决策的随机程度。若决策者对自身的先验概率把握不准，或者某些自然状态发生了改变，决策者对未来发展很不确定的时候，都可以通过贝叶斯模型对其进行分析，对先验概率进行修正，通过综合对比，选取最优决策方案，降低企业的决策风险。

4 总结

将贝叶斯公式应用于企业的新工艺引进决策分析中，通过市场销售调查获得不同决策方案下的先验概率，并在此基础上通过贝叶斯公式对其进行修正，得出后验概率分布情况，最后将不同自然条件下不同决策方案的平均盈利值进行对比，获得最佳决策方案。

影响企业决策的因素有很多，贝叶斯分析是企业随机决策分析中最常用的方法之一，它的判断基准是期望效用最大。企业在使用时必须先对企业的实际情况和相关市场信息作出正确的估计，只有这样，企业才能通过贝叶斯模型作出正确的决策，才能使企业效益最大化，风险最小化。

[1]姜颖，王晓锋.以概率论的视角理性看待社会热点[J].沈阳师范大学学报：自然科学版，2012，30（1）：27-31.

[2]盛骤，谢式千，潘承毅.概率论与数理统计[M].北京：高等教育出版社，2008.

[3]李德荣，刘鹤.关于全概率公式和贝叶斯公式的一种新讲解[J].内蒙古统计，2009（6）：42-43.

[4]张嵘.浅谈后验概率在信息选取和随机决策中的应用[J].商业经济，2012（10）：36-38.

[5]杨静，陈冬，程小红.贝叶斯公式的几个应用[J].大学数学，2011，27（2）：166-169.

[6]许谨良.随机管理[M].北京：中国金融出版社，2006.

[7]陈立文.项目投资随机分析理论与方法[M].北京：机械工业出版社，2004：119-126.

〔责任编辑 高海〕

Stochastic Decision Analysis of Introducing New Production Lines based on Bayes Formula

WU Jun-lan
（Xinzhou Normal University，Xinzhou Shanxi，034000）

Stochastic decisions exist in the production and management of enterprises anywhere and any time.Whether the scochastic decision is reasonable depends on whether the information of decision making is used efficiently.Bayes formula can combine the information about themodel，data and priori in order to help managers get best decisions.This paper introduces Bayes formula and related concepts，explains the application of Bayes formula，which provides some instructions for stochastic decision management of enterprises.

Bayes formula；stochastic decision；information

O212.4

A

1674－0874（2013）06－0012－03

2013-07-28

武俊兰（1974-），女，山西五台人，讲师，研究方向：数学教育。