地面三维激光扫描仪的测量误差分析
杨忞婧
(东华理工大学测绘工程学院,江西抚州 344000)
随着信息时代的日新月异以及计算机技术的迅猛发展,三维激光扫描技术的出现使得人们可以深入到复杂的现场环境及空间中进行扫描操作,并可以直接实现各种大型的、复杂的、不规则的、标准或非标准的实体或实景三维数据完整的采集,进而快速重构出实体目标的三维模型及线、面、体、空间等各种制图数据 (马立广,2005,李清泉等,2003;贺亮等,2011;张亚,2011)。三维激光扫描仪由最初的点对点激光测距发展到采用非接触式主动测量的方式快速扫描目标物体并获取表面点的三维信息。三维激光扫描技术的发展也使得人们从使用传统方式获取人工单点数据变成了连续自动获取批量数据,大大地提高了工作效率和测量精度。
1 三维激光扫描仪测量原理
扫描仪集成了多种高新技术,采用非接触式主动测量方式,以获取点云的形式测量地形及复杂物体表面点集的三维数据。三维激光扫描仪主要采用脉冲测距法来计算出点的三维坐标。
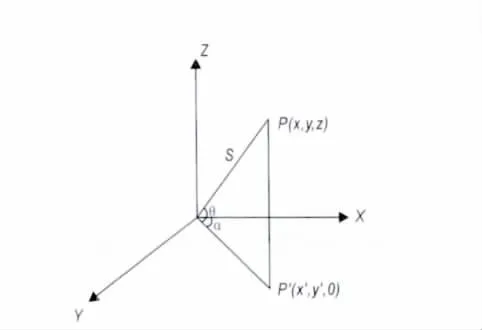
图1 三维激光扫描系统测量原理Fig.1 3D laser scanning system measuring principle
三维激光扫描仪内部坐标系统由横向扫描面内的X,Y轴以及纵向扫描面内的Z轴组成,其中X轴与Y轴垂直,Z轴垂直与横向扫描面。P点为被测点,通过脉冲测距法可得距P点的距离观测值为S,仪器内的精密时钟控制编码器同步获取激光脉冲的横向扫描角度α和纵向扫描角度θ。P′是P点在XY面上的投影点(图1)。
P点的三维坐标计算公式:

地面三位激光扫描仪常用的测距方法有脉冲测距法、三角测距法和相位测距法。
(1)脉冲测距法。通过激光扫描仪发射出的脉冲信号抵达物体表面后反射回扫描仪信号接收器所产生的时间差△t,可以计算信号往返的路程:S+d=1/2×△t×c,其中c为光速,d为二极管到反光镜的距离,S为扫描仪到物体的距离。当测量的距离较远时,d相对于S非常的小,可以忽略,即S=1/2×△t×c;当测量距离较近时,测距精度相对较差,因此,时间差测量法适合远距离测距,但是总体而言,测距误差随距离的增加而增加(图2)。

图2 时间差测量法Fig.2 Time difference measurement method
(2)三角测距法(程光亮等,2007)。已知扫描仪到凸透镜的基线距离D,由扫描仪发射激光信号在物体表面的入射光线与反射光线的夹角为β。在基线的另一端设置CCD来接收物体的反射激光信号,通过三角形的几何关系推算出扫描仪到物体之间的距离。若扫描仪在水平方向发射激光信号至物体表面,则可推算出扫描仪到物体的距离:S=D/tanβ(图3)。
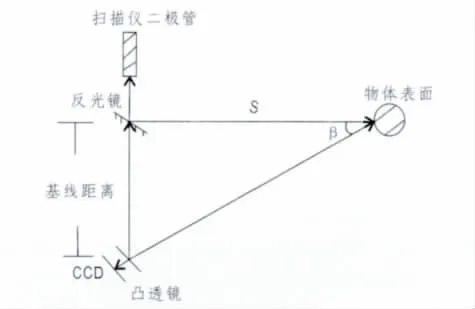
图3 三角测量法Fig.3 Triangle measuring method
(3)相位测距法(周睿等,2009)。用无线电波段的频率,对激光束进行幅度调制,通过测定调制光信号在被测距离上往返传播所产生的相位差,间接测定往返时间,并进一步计算出被测距离。相位测距法是一种间接测距方法,通过检测发射和接受信号之间的相位差,获得被测目标的距离(张启福等,2011)。该方法的精度较高,但是主要通过两个间接测量测得距离,因此三维激光扫描仪中使用这个方法测距的较少。
2 三维激光扫描仪测量误差分析
三维激光扫描仪测量误差从误差理论来分析,可以分为系统误差、偶然误差。由于系统误差具有积累性(潘正风,2004),因此系统误差可以通过公式改正或者用一定的测量方式抵消。偶然误差具有随机性,是人为无法控制的,但是可以采用多次重复观测,取其平均数来抵消。
三维激光扫描仪测量误差还可以分为三类:仪器误差、目标物体反射面相关误差、多路径误差和外界条件引起的误差。
2.1 仪器误差
这类误差往往来自于仪器本身,由于仪器本身的性能缺陷使得测量值与实际值之间存在一定的误差,包括激光测距的误差、扫描角度误差。
(1)激光测距误差。激光发射器向目标物体发射激光脉冲信号,在目标物体表面会形成一个激光光斑,目标物体距扫描仪越远,光斑直径d越大。理论上认为,扫描仪测量的距离应该是激光中心轴线投射到目标上位置所对应的数据S,但实际测量时,扫描仪获得的数据是根据第一次回波来确定的,而该反射点可以是光斑范围内的任意位置,因此误差往往与测距长度S成正比,距离S越长,误差越大,称为“比例误差”;由于测距系统内部激光发射器与反光镜之间还存在一定的距离,使得测得的距离与实际距离存在一个固定的差距,称为“固定误差”,用公式来表示:
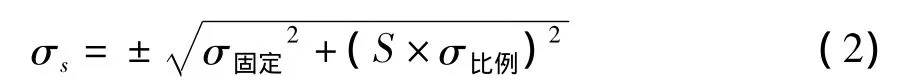
(2)扫描角度的误差。扫描角度误差包括水平扫描角度和竖直扫描角度的误差。扫描角度引起的误差主要来自于扫描镜面平面角误差、扫描镜转动的微小震动、扫描电机不均匀转动控制误差等因素的综合影响(郑德华等,2005)。如图4所示,由于光斑的存在产生偏角θ,tanθ=(d/2)/S,由于θ非常小,所以θ=d/(2S)。
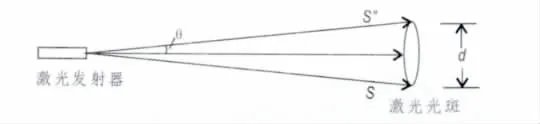
图4 激光光斑引起测距误差Fig.4 Laser range error caused by laser- spot
2.2 目标物体反射面相关误差
这类误差往往来自于被扫描的目标物体,扫描仪激光发射器发出脉冲信号,抵达目标物体反射面后会发生激光反射,该过程中会因为反射面倾斜或者表面粗糙不光滑而导致测量的距离和角度发生一定的偏差。
(1)反射面倾斜产生的误差。如图5所示,激光光斑直径为d,激光发射孔径为D,激光光束发散角为2α,S为发射孔径到目标物体表面的距离。由此可求出光斑直径大小:
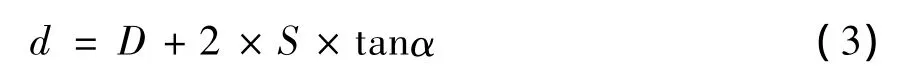
当目标物体反射面发生倾斜时,倾斜面与原反射面形成夹角。假设反射面倾斜时量测的距离为S″,可知:

为了方便计算,假设孔径D为0,

由于α非常小,因此sinα≈α,若ds为激光光斑引起的最大偏差,则
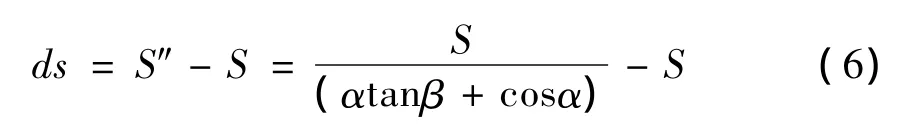
可以看出误差随距离S、激光发散角度2α、目标物体反射面倾斜角度β变化而变化。
郑德华等(2005)得出目标物体反射面倾斜引起的最大偏差,其中γ是激光发散角,S为发射孔径到目标物体表面的距离。
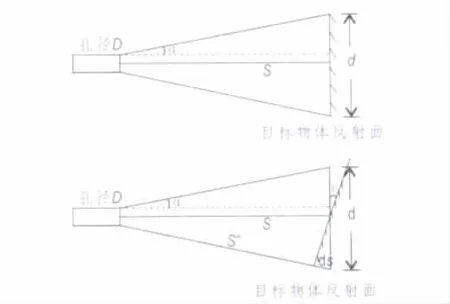
图5 目标物体反射面倾斜引起的误差.5 The error caused by target object reflective surface tilt
(2)反射面粗糙产生的误差。三维激光扫描仪接收的回波脉冲信号可能是激光抵达目标物体反射面后首次反射回来的信号,也可能是最后一次反射回来的信号。若按照首次回波信号来处理,那么目标物体反射面粗糙产生的距离误差ds近似于反射面粗糙最大值dmax的1/2(图6)。

图6 目标物体反射面粗糙引起的误差Fig.6 The error caused by target object reflective surface coarse
2.3 多路径效应产生的误差
当激光扫描仪对目标物体边缘进行扫描时,产生的光斑落在目标物体边缘上。系统接收到一部分由被测目标物体边缘表面A点反射回来的能量,以及另一部分由交界处的相邻物体边缘表面B点反射回来的能量,两种不同的反射能量发生干涉,使得系统测距结果产生误差(王应东,2011)。如果目标物体边缘交界处其他物体在激光扫描仪有效测程以外,如图7中所示C点,那么系统只能接收到落在目标物体边缘的部分光斑内的能量,因此无法获得该交界点的测量信息。
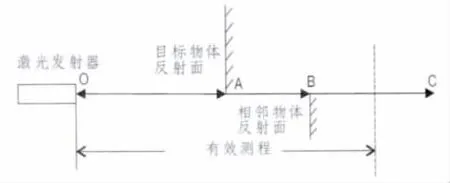
图7 多路径产生误差示意图Fig.7 The error caused by multipath
2.4 外界环境
该类误差往往来自于外界环境中的空气温度、气压、湿度等客观因素。空气温度、气压、湿度会对光在空气中的传播有一定的影响,当测量距离较远时,光在空气中传播速度、传播方向都会存在一定的偏差,因此三维激光扫描仪需要在一定温度范围内工作才能获得精确的数据。
3 三维激光扫描仪测量点位误差模型
已知测得某点的距离观测值中误差为ms,水平扫描角度观测值中误差为mα,竖直扫描角度观测值中误差为mθ。其中,n为观测次数,v是观测值的改正值分别为算术平均值。

一组观测值取算术平均值之后,改正值之和恒等于零 (潘正风,2004),作为数据校验的依据。
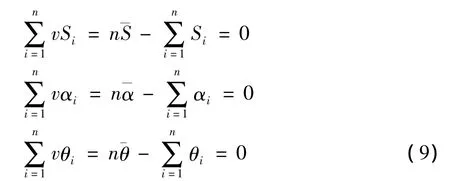
根据白塞尔公式(潘正风,2004)可求得距离、水平扫描角度和竖直扫描角度的中误差:
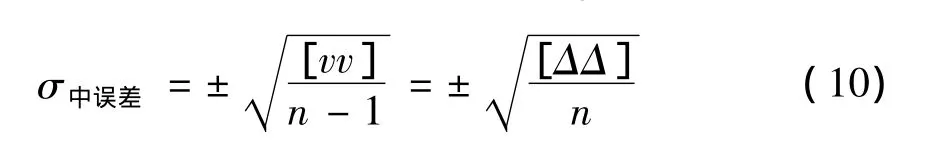
点位X轴方向的误差模型为:

点位Y轴方向的误差模型为:

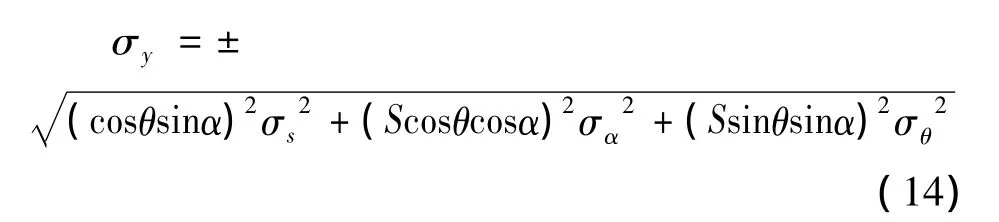
点位Z轴方向的误差模型为:

点位误差模型为:
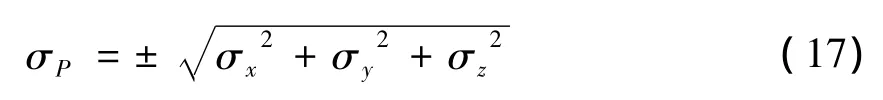
4 实验数据及分析
本次实验地点选择在某高校广场上,该处视野宽阔,无遮挡,地面近似水平。时间选择在外界环境变化小且周围人流量较少的一段时间内。首先在O点架设高精度的全站仪,整平对中后瞄准1号点位上的标靶中心进行定向,方位角设为0°,记录距离值和坐标值。再分别瞄准2,3,4,5,6号点位的标靶中心,获取6个点的坐标、距离以及方位角。卸下全站仪后,将三维激光扫描仪架设于O点,整平对中后扫描。在整个实验过程中,被扫描的标靶位置不变,使用的标靶均由相同反射率的材料制成。扫描后的数据用Riscan pro软件处理,获得O点扫描仪到6个点位上标靶中心之间的距离,以及点位上标靶中心之间扫描时转动的水平角(表1)。
由公式(10)可以解算到测距中误差为0.7 mm测角中误差为0.0003°符合精度要求(表2)。
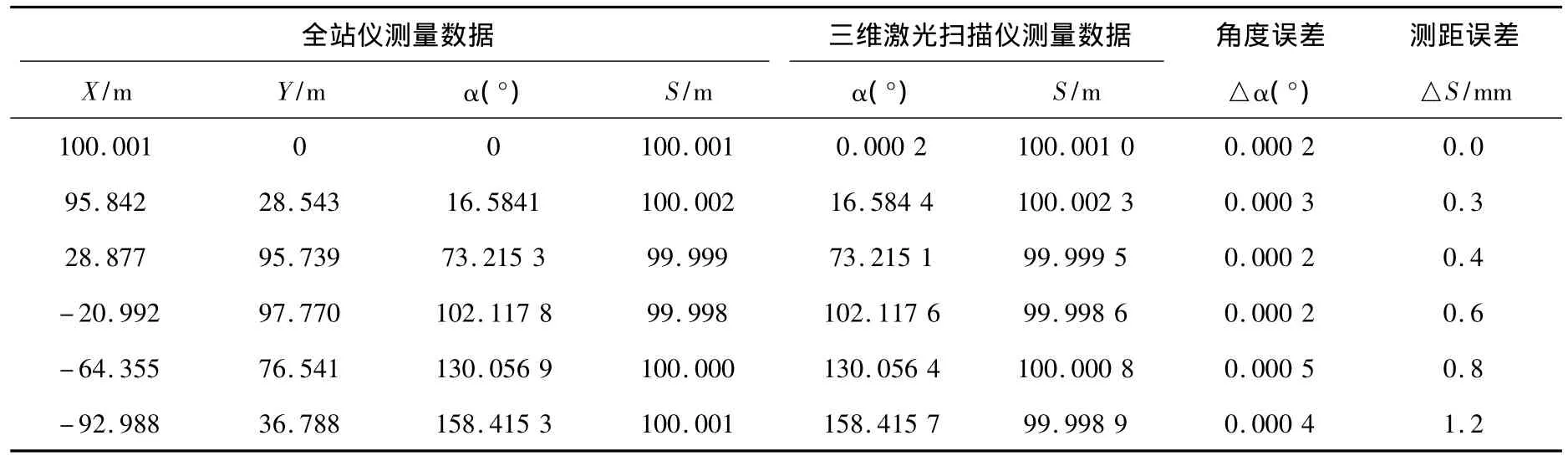
表1 全站仪与三维激光扫描仪测量数据对比Table 1 The contrast of tachometer and 3d laser scanner measurement data

表2 三维激光扫描仪REIGL-VZ400主要参数Table 2 3Dlaser scanner Reigl-vz400 major parameter
5 结语
三维激光扫描仪在诸多领域得到了广泛应用,尤其在三维重建在数字地球、数字城市和虚拟现实等领域的应用、更为广泛。该技术集合了高分辨率、高准确度、高效率等多种技术优点。随着社会的发展,科学技术的进步,三维激光扫描仪将会凭借其数据获取速度快、外业作业时间短,自动化程度高,操作方便等优点逐渐替代传统测量仪器。当然,和传统测量仪器一样,三维激光扫描仪的应用也面临着测量误差的影响。通过对三维激光扫描仪的误差分析,认为在实际应用中,要选择满足精度要求的三维激光扫描仪进行量测。
程光亮,张福利,王宝山.2007.3维激光扫描技术在工程应用中的精度探讨[J].测绘与空间地理信息,30(4):25-32.
贺亮,刘荣,吕开云.2011.一种基于种子生长的匹配算法[J].东华理工大学学报:自然科学版,34(4):379-383.
李清泉,杨必胜,史文中,等.2003.三维空间数据的实时获取、建模与可视化[M].武汉:武汉大学出版社:1-19.
马立广.2005.地面三维激光扫描测量技术研究[D].武汉:武汉大学硕士学位论文.
潘正风.2004.数字测图原理与方法[M].武汉:武汉大学出版社:42-50.
王应东.2011.GPS误差分析和精度控制[J].测绘与空间地理信息,34(6):235-236.
张启福,孙现申.2011.三维激光扫描仪测量方法与前景展望[J].北京测绘,(1):39-42.
张亚.2011.三维激光扫描技术在三维景观重建中的应用研究[D].长安大学硕士学位论文.
郑德华,沈云中,刘春.2005.三维激光扫描仪及其测量误差影响因素分析[J].测绘工程,14(2):32-35.
周睿,孔东.2009.一种高精度相位激光测距方法的实现[J].科学技术与工程,9(21):6337-6342.

