SBI与RRI结合的MT二维反演方法研究及应用

叶益信， 邓居智， 杨海燕， 李泽林， 何梅兴

(1.东华理工大学放射性地质与勘探技术国防重点学科实验室，江西抚州 344000;2.中国地质科学院地球物理地球化学勘查研究所，河北廊坊 065000)

目前，MT数据的正反演方法取得了很大进展(吴信民等，2013)，二维反演方法更是百花齐放，种类繁多，但是大多数二维反演都得到光滑模型结果，如 OCCAM、RRI、REBOCC、NLCG 等(Constable et al.，1987;deGroot-Hedlin et al.，1990;Smith et al.，1991;Siripunvaraporn et al.，2000;Rodi et al.，2001)，这些方法对边界位置的拟合较差，尤其是石油勘探中常常遇到大块均匀电导率的电性单元电阻率差异较大情况，如何快速稳定地得到反演结果和更清晰的电性分界面仍是当前MT反演研究的一个重点问题。

为了克服光滑模型反演结果边界位置模糊不清的问题，Smith等(1999)提出了反演二维MT数据的SBI方法，deGroot-Hedlin(2004)研究了用于反演二维MT数据的SBI算法，并认为这种算法的优点是能得到不同层的下底边界深度及其电阻率值，但这种算法的收敛性较差，除非给一个好的初始模型;Zhang等(2010)对该方法做了改进研究，通过引入对角梯度支撑改善了倾斜电性分解面的反演效果;杨长福等(2005)对该方法作了阐述，并与国际流行的二维反演方法作了对比研究。Smith等(1991)开发的RRI算法是我国MT工作者最为熟悉的一种二维反演方法，快速是其最大的优点，但是它对复杂结构的反映往往不是很准确。胡祖志等(2005)对该方法与国际上通用的二维反演方法作了对比研究。由于各种方法各有其优缺点，研究两种或两种以上方法的结合反演是当前反演的一个热点问题，欧东新等(2005)将SBI方法的模型构建方式和RRI方法结合起来，提出了一种新的二维快速反演方法;Zhang等(2008)就SBI法与OCCAM法结合反演做过有意义的工作。本文采用RRI法与SBI法结合反演的办法，先通过RRI反演得到一个光滑模型，然后采用模糊聚类方法得到一个合适的反演初始模型，再进行SBI反演，最后得到一个折中的反演结果。通过理论模型试算、对比分析及实测资料反演对比，表明了该方法的可行性和有效性。

1 方法原理

1.1 SBI反演基本原理

SBI反演从模型构建上着手，把地质结构看成由有限数量具有均匀电导率的电性单元组成，而这些单元的深度在横向上是可变的，模型参数用各单元的电阻率值及其下底边界深度表示，对于一个包含i层每层含n个最小单元的半空间模型，模型参数m可描述为:

式中ρi为第i层的电阻率，din为第i层第n个单元下底界面的深度，由于各参数的变化范围较大，为了反演的稳定性，采用它们的对数值进行反演。

反演目标函数为

通过求导得到模型参数的迭代系列为

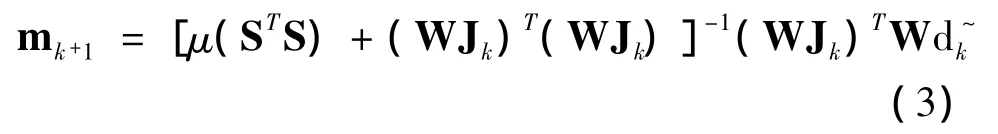
对于给定的初始模型，可以通过这个迭代系列寻找极小可能构造模型(deGroot-Hedlin et al.，2004;欧东新等，2005;叶益信等，2009)。

1.2 RRI反演基本原理

RRI反演通过解与一维相近的反演问题，来计算在每个测点位置下面的电阻率扰动，把二维反演问题转化为一系列一维反演问题。

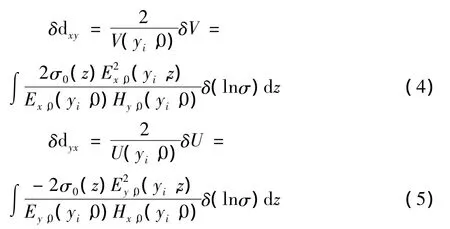
其中δdxy和δdyx分别为TE和TM模式下观测数据与理论数据的差值，σ0(z)为模型改变前的电导率值，Hy，0(yi，0)，Ex，0(yi，0)，Hx，0(yi，0)和 Ey，0(yi，0)分别是模型改变前第i个测点下地表的磁场值和电场值，Ey，0(yi，z)和 Ex，0(yi，z)是初始模型或者本次迭代前模型在第i个测点下某深度的理论电场。

综合考虑模型横向和垂向的不均匀性，构造如下目标函数:

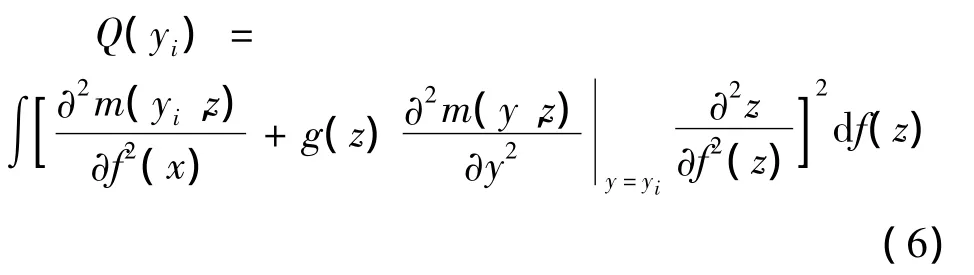
这是一个在各测点上的标度Laplace范数。式中，函数f(z)可以控制标度尺的长度，是用来度量不同深度的构造，取f(z)=ln(z+z0)，常数z0通常是选取模型表层电阻率值和最高频率情况下的趋肤深度。m=ln(σ)= －ln(ρ)。g(z)是起控制水平方向构造的惩罚因子(高才坤等，2009)。

1.3 RRI与 SBI结合反演

从上面原理可以看到，由于两种反演的模型参数不同，所以不能把两种方法以加权的形式放在一起加以计算。因此我们先对数据作RRI反演，从半空间模型开始，得到一个较光滑的模型结果，记该结果为m1。将m1作为SBI反演的初始模型进行SBI反演，得到反演结果m2，将m2作为最终反演结果。由于m1是一个以不同测点不同深度电阻率表示的结果，而SBI反演的初始模型为块状结构模型，因此需要把m1转化为块状结构模型。本文采用模糊聚类方法将m1转化为块状结构模型。模糊聚类方法的原理如下:

将数据集分成L组，则可把数据集表示成:Xij(i=1，…，N;j=1，…，M)，在构建反演初始模型时，N表示电阻率的个数，M通常等于3(电阻率的值、y、z的坐标)，L表示要构建初始模型的层数;那么数据集第j个矢量在第i类的成员函数可表示为:U=［Uij］LXN(U也称分割矩阵);将数据集模糊聚类成L类的函数满足以下条件(George et al.，2004):

然后通过解不含约束条件的目标函数(Salski，2007):

式中，V=［v1，…，vL］(1 ＜ L ＜ M)为类的中心位置矢量，P为控制录属度权重的因子，‖·‖为范数，解上述目标函数使其达到最小，可得类的中心位置及各自成员函数的表达式。(8)式中的X矢量表示RRI反演结果的模型参数，V矢量表示SBI反演的初始模型参数。

2 模型试验

2.1 模型Ⅰ试验

模型Ⅰ为一孤立体模型(图1a)，一半空间存在一个异常体，电阻率为10 Ω·m，尺寸为1.6 km×0.8 km，顶面埋深800 m，半空间背景电阻率为100 Ω·m。测点个数为11，采集36个频点(1 441，1 024，721，512，360，256，180，128，90，64，45，32，22.5，16，11.3，8，5.6，4 2，1.4，1，0.7，0.5，0.32，0.25，0.176，0.125，0.088，0.06，0.044，0.03，0.022，0.015，0.011，0.007，0.005)Hz，有限元正演网格为58×52。先用RRI法进行反演(图1b);然后用SBI法进行反演(图1c);最后采用RRI与SBI结合的反演(图1d)。从反演结果图可看出，RRI反演结果对异常体的结构反映模糊，没有反映出异常体的确切电阻率和边界位置，SBI反演结果能反映出异常体的确切电阻率和边界位置，但是其边界轮廓有很多毛刺现象，不够光滑，而RRI与SBI结合的反演结果不但可反映出异常体的确切电阻率和边界位置，且其边界轮廓更加光滑，与模型真实电阻率和边界位置更加接近。从它们的迭代拟合差曲线变化(图2)也可看出，RRI反演收敛速度较慢且其拟合差较大，SBI反演次之，采用RRI与SBI结合的反演收敛速度更快，其拟合差与SBI反演相当。

2.2 模型Ⅱ试验

图1 孤立体模型反演结果比较Fig.1 Single blocked model and inversion results

模型Ⅱ为一楔形体模型(图3a)，包括四个电性单元，分别为:第一电性单元100 Ω·m，位于地表层;第二电性单元1 000 Ω·m，位于中间层左侧;第三电性单元10 Ω·m，位于中间层右侧;第四电性单元100 Ω·m，位于底层。正演计算时的频点和网格与模型Ⅰ正演计算时一致，接收点共11个，点距为400 m。分别对数据进行 RRI、SBI及SBI与RRI结合的反演，从它们的反演结果(图3b，c，d)可以看出，RRI反演结果只能反映各个电性单元的大致电阻率值及电性分界面的大致形态，且对深部电性单元结构反映不准;SBI反演结果能基本反映各个单元的电阻率及其电性分界面，但是对模型边界位置的拟合稍差;两种方法的结合反演不仅可以反映各个单元的电阻率，而且对模型边界位置的拟合更好。它们的拟合差变化曲线变化与模型Ⅰ试验结果具有相似的结论。

图2 迭代拟合差变化曲线图Fig.2 Misfit error curves with iterations of different inversion approaches

图3 楔形体模型反演结果比较Fig.3 Wedge model and inversion results

3 实测数据反演应用

最后，采用该方法对一条实测MT数据进行了反演，实测数据为武汉周边地区地热勘察的大地电磁数据，该数据包含测点19个，频点个数为34个，范围从320 Hz到0.035 Hz，点距保持在200 m左右，总剖面长3.62 km。在反演开始前，首先对获得的数据进行二维滤波处理。先用RRI法对该数据进行了反演(图4)，然后再进行SBI与RRI结合的反演，两种反演结果的拟合差分别为20 rms和14.7 rms，表明结合反演的拟合差较小。通过结合反演结果与RRI反演结果的对比可看出，结合反演结果电性分离更明显，电性界面位置更清晰。从图4a可看出，该地区可分为四个电性单元:第(1)电性单元电阻率为50左右，分布于地表，厚度约0.1～0.2 km;第(2)电性单元电阻率1 000以上，分布于深度0.1～1.3 km之间，中间厚两边薄;第(3)电性单元电阻率为77左右，分布于横向0～1.5 km深度0.5 ～1.5 km 范围和横向3 ～3.6 km 深度0.7～1.7 km范围;第(4)电性单元电阻率为790左右，分布于深度1.5 km以下范围。根据区域地质资料，第(1)电性单元对应为第四系覆盖层;第(2)电性单元上部有三叠系的地层，下部主要为二叠系的下统栖霞组、孤峰组及二叠系上统龙潭组、大隆组地层，岩性对应为硅质页岩、粉砂岩、炭质页岩、炭质灰岩，电阻率相对呈高阻反应;第(3)电性单元对应为三叠系的大冶组和嘉陵江组，岩性对应为白云质灰岩、泥质灰岩、砂质页岩，电阻率相对呈中低阻反应;第(4)电性单元主要为石炭系黄龙组、泥盆系上统五通组、志留系中统坟头组，岩性对应为生物碎屑灰岩、白云质灰岩、泥质灰岩、石英砂岩夹粘土岩、石英质砾岩、粉砂质泥岩、细砂岩、石英砂岩，电阻率相对呈中高阻反应。通过将反演结果与地质资料比对，表明反演结果与地质资料吻合的较好。

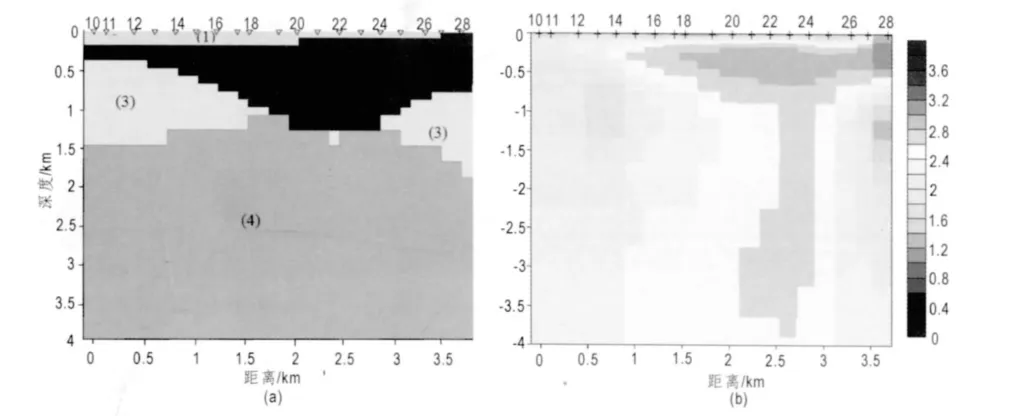
图4 实测数据反演结果对比Fig.4 Real data inversion results

4 结论

(1)通过引入模糊聚类算法，将SBI和RRI反演结合起来反演，弥补了各自的局限性，同时发挥了各自的优点。

(2)通过理论模型试算表明，与各自单独反演相比，SBI和RRI的结合反演收敛速度更快，反演精度更高，对电性分界面特征反映效果更好。

(3)对武汉某测区一条实测MT资料的处理对比分析表明，这种方法的具有一定的实用性。

胡祖志，胡祥云，吴文鹏，等.2005.大地电磁二维反演方法对比研究［J］.煤田地质与勘探，33(1):64-68.

高才坤，汤井田，王烨，等.2009.基于RRI反演的高频大地电磁测深在深边部矿产勘探中的试验研究［J］.地球物理学进展，24(1):309-314.

欧东新，王家林.2005.二维块状结构大地电磁快速反演［J］.石油物探，44(5):525-528.

吴信民，杨海燕，杨亚新，等.2013.论电法勘探的理论探测深度［J］.东华理工大学学报:自然科学版，36(1):60-64.

杨长福，徐世浙.2005.国外大地电磁研究现状［J］.物探与化探，29(3):243-247.

叶益信，胡祥云，金钢燮，等.2009.大地电磁二维陡边界反演应用效果分析［J］.地球物理学进展，24(2):668-674.

Constable S C，Parker R L，Constable C G.1987.Occam’s inversion:A practical algorithm for generating smooth models from electromagnetic sounding data［J］.Geophysics，52(3):289-300.

deGroot-Hedlin C，Constable S C.1990.Occam’s inversion to generate smooth two-dimensional models from magnetotelluric data［J］.Geophysical，55(12):1613-1624.

deGroot-Hedlin C，Constable S C.2004.Inversion of magnetotelluric data for 2D structure with sharp resistivity contrasts［J］.Geophysics，69(1):78-86.

George E，Tsekourasa，Haralambos Sarimveisb.2004.A new approach for measuring the validity of the fuzzy c-means algorithm［J］.Advances in Engineering Software，35:567-575.

Rodi W L，Mackie R L.2001.Nonlinear conjugate gradients algorithm for 2D magnetotelluric inversion［J］.Geophysics，66(1):174-187.

Salski A.2007.Fuzzy clustering of fuzzy ecological data［J］.Ecological Informatics，(2):262-269.

Siripunvaraporn W，Egbert G.2000.An efficient data-subspace inversion method for 2-d magnetotelluric data［J］.Geophysics，65(3):791-803.

Smith J T，booker J R.1991.Rapid inversion of two-and three-dimensional magnetotelluric data［J］.Geophys，Res.，96:3905-3922.

Smith T，Hoversten M，gasperikova E，et al.1999.Sharp boundary inversion of 2D magnetotelluric data［J］.Geophysical Prospecting，47:469-486.

Zhang L L，Yu P，Wang J L，et al.2008.Two-dimensional magnetotelluric inversion in combination of smoothest model and sharp boundary［C］//19th IAGA WG 1.2 workshop on electromagnetic induction in the earth，Beijing.

Zhang L L，Yu P，Wang J L，et al.2010.A study on 2D magnetotelluric sharp boundary inversion［J］.Geophys，(in chinese)，52(3):631-637.