局部高斯尺度混合模型的傅里叶－小波图像降噪

唐 锐，张敬东，张 祺

(1．攀枝花学院机电工程学院，四川 攀枝花617000，2．攀枝花学院交通与汽车工程学院，四川 攀枝花617000)

1 引言

数字图像的噪声主要来源于图像的获取(图像的数字化)和传输过程。图像传感器的工作情况受各种因素的影响，如图像获取中的环境条件和传感元器件本身的质量。图像在传输过程中主要由于受传输信道的干扰而受到噪声污染。

噪声的污染使图像偏离了真实景况，极大影响了人们从图像中提取信息，因此，非常有必要在利用图像之前消除噪声。常规的图像消噪方法主要有两类［1－7］:一类是基于频域，针对整幅图像的全局处理;另一类是基于空间域，针对图像中某一像素中邻域的局部处理。这两类消噪处理要么完全在频率域，要么完全在空间域展开。这两类消噪处理方法造成了顾此失彼的局面，虽然抑制了噪声，却损失了图像边沿细节信息，造成图像模糊。

傅里叶变换从整个时域(空域)上分析信号的频谱信息，却不能反应信号在局部时间范围内的特性，缺乏信号的局部化分析能力有效地表示图像中的突变部分。

小波分析在时间域和频率域都具有良好的局部特性可以聚焦到信号的任意细节，小波分析恰好改变了这种局限性。

为了获取较好的降噪效果，文献［2］提出了一种傅里叶－小波降混合噪方法并获得了良好的效果。文章在文献［2］的基础上，采用局部高斯尺度混合模型描述降噪图像的小波变换系数的统计特性［7－14］，进行不含噪图像的小波系数估计，修改小波系数，该方法考虑了图像中含有噪声的相关性，使得降噪效果比传统方法进一步提高。

2 傅里叶变换

一般性考虑给定非周期实函数信号f(t)，f(t)∈L2(R)的连续傅里叶变换及逆变换的定义为:

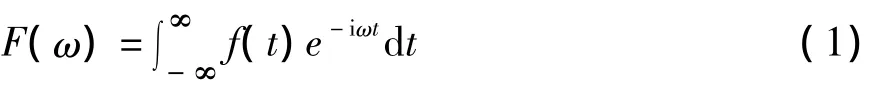
F(ω)取决于f(t)在整个积分区间的整体性质，其从整个时域(空域)上分析信号的频谱信息，却不能反应信号在局部时间范围内的特性，缺乏信号的局部化分析能力。傅里叶变换可以分别时域和频域分析问题，但不能同时在时域和频域考察。这些正是傅里叶变换存在的弱点。

3 小波变换

傅里叶变换对时间域上的信号进行频谱分析时，当从时域变换到频域时所有的时域特征就会失去，对于非平稳信号的分析有一定的局限性，而对信号进行小波变换并不会改变它的时间特性，而且小波分析在时间域和频率域都具有良好的局部特性可以聚焦到信号的任意细节，小波分析恰好改变了这种局限性。

小波ψ(t)∈L2(R)，其傅里叶变换为Ψ(ω)，当Ψ(ω)满足容许性条件:

时，称ψ(t)为一个小波基函数或母小波。将母函数经伸缩和平移后，就可以得到一个小波序列，由其可生成的小波序列可表示为:

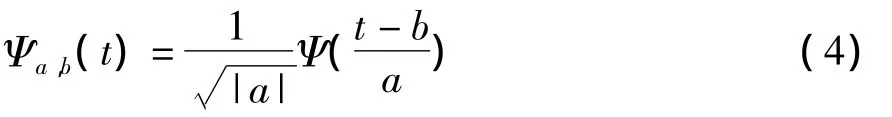
其中，a为缩放因子(对应于频域信息);b为平移因子(对应于时空信息)。

任意能量有限函数f(t)，f(t)∈L2(R)的连续小波变换定义为:

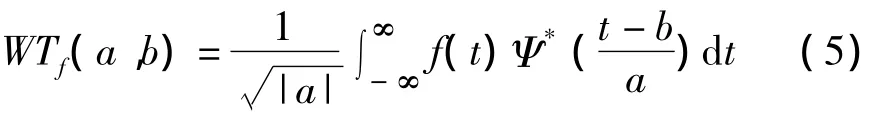
其逆变换为:

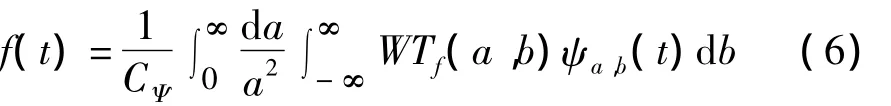
式中，ψ*(t)表示ψ(t)的复数共轭。

4 局部高斯尺度混合模型

局部高斯尺度混合模型如图1所示，图中y为一个局部邻域内含噪声图像的小波变换系数的随机向量，w和u均为零均值的小波变换系数的高斯随机向量，其协方差矩阵可分别记为Cu和Cw，z为标量乘数因子，其概率密度分布函数为:

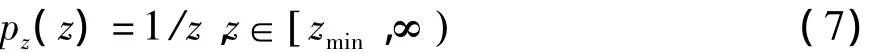
高斯尺度模型的数学表达式为:

由此可得，在确定的z的概率密度分布函数的条件下，y是一个零均值的高斯随机向量，其协方差阵为:

若 E(z)=1，则:

图1 局部高斯尺度混合模型Fig．1 local Gaussian scale mixtures model

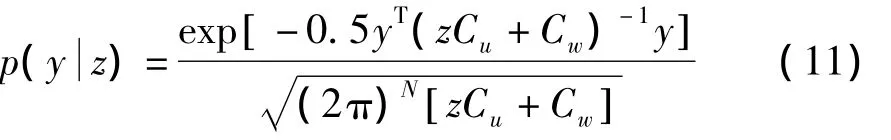
图像的降噪是在每一个局部邻域内，从噪声图像的小波变换系数的随机向量y中估计出局部邻域中心的原始图像的小波系数xc，xc的最小平均平方误差估计在y的条件下的数学期望为:

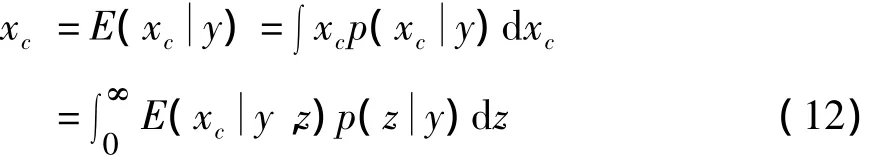
其中:

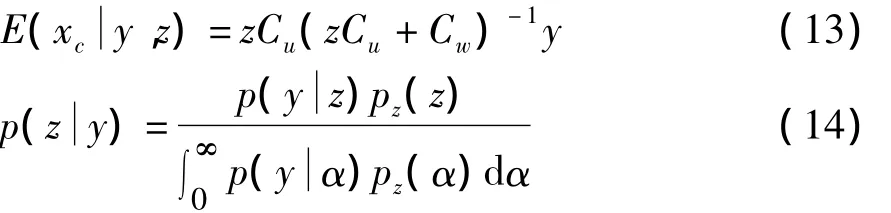
基于上述分析，本文采用一种融合傅里叶变换和小波变换的方法对图像进行降噪，即基于局部高斯尺度混合模型的混合傅里叶－小波降噪法，其算法步骤如下:

(1)傅里叶变换图像降噪:估计原始图像的功率谱密度，分析原始图像的能量分布情况;

(2)小波变换图像降噪:

Ⅰ将傅里叶变换降噪后的图像作小波变换，获得图像的小波变换系数，将图像分解为多个子频带信号;

Ⅱ按照GSM法修改小波系数协方差阵，对每一个邻域进行估计，估计出局部邻域中心的原始图像的小波系数，进而获得不含噪声的图像的小波变换系数的估计;

Ⅲ将修改后的小波变换系数作小波逆变换，获得降噪后的图像。

5 实验方法与结果

为了更好地验证和比较本文所用方法的性能，我们将此方法用于两个8位灰度图像Barbara，Boat上，其中，Barbara图像具有较多的纹理和缓慢变化的部分，Boat图像是一个有鲜明背景、包含较多的尖锐变化的户外图片。实验分两部分进行，第一部分为分别对图像Barbara，Boat添加不同标准偏差(σ)的随机噪声，采用局部GSM模型混合傅里叶－小波法降噪时选用不同的小波，即Db3，Db4，Db5，Db6，Db8，Db10对加噪图像进行降噪。第二部分为在第一部分所得结果的基础上和局部自适应维纳滤波(LAWMAP)、贝叶斯最小平方－高斯尺度混合模型(BLS-GSM)、混合傅里叶－小波等方法作比较。

此处使用的衡量降噪效果的指标是PSNR(peak signal to noise ratio)，其定义如下:

式中，Xi为原始图像的第i个像素值;X为降噪后图像的第i个像素值，该指标为客观标准，没有反映人类对图像质量的视觉感受，主要用于8位灰度图像的降噪评估中。采用本文所用的方法对图像Barbara，Boat进行降噪后的PSNR分别如图2、图3所示。

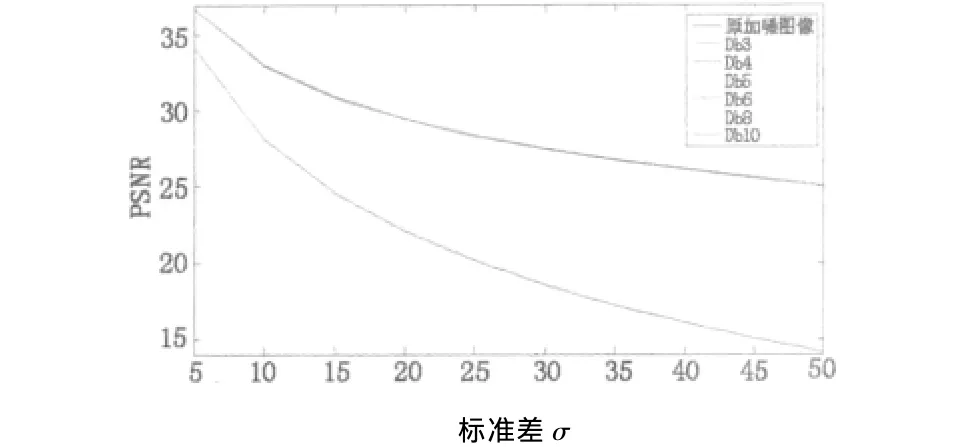
图2 LGSMM混合傅里叶－小波降噪Barbara图像的PSNR值Fig．2 PSNR of Barbara using themethod proposed

图3 GSM混合傅里叶－小波降噪boat图像的PSNR值Fig．3 PSNR of Boat using themethod proposed

图4和图5分别显示的是噪声标准偏差σ=30时的图像Barbara，Boat进行降噪后的效果。不同方法对加不同噪声偏差的图像Barbara降噪处理后的对比图如图6所示。

图4 图像降噪效果(Barbara，σ=30)Fig．4 effect of imagede-noising(Barbara，σ =30)

图5 图像降噪效果(Boat，σ=30)Fig．5 effect of imagede-noising(Boat，σ =30)

图6 采用不同方法降噪效果对比图(Barbara)Fig．6 contrast diagram of noise reduction effects using different methods( Barbara)

(1)从图2和图3中可以看出，采用本文提出的基于局部高斯尺度混合模型的混合傅里叶－小波对图像Barbara，Boat进行降噪时，原始加噪图像的PSNR和使用不同小波降噪后图像的PSNR均随着噪声标准偏差σ的增大而减小，但使用不同小波降噪后图像的PSNR减少速率要缓慢，这表明原始加噪图像的噪声标准偏差σ越大，降噪效果越明显。同时可看到采用基于局部高斯尺度混合模型的混合傅里叶－小波对图像Barbara，Boat进行降噪时，选择不同的小波函数，图像Barbara，Boat降噪后的PSNR线几乎重合。

(2)当噪声标准偏差σ=30时，从图4和图5中左右两幅图片显示效果的比较中可看到采用本文方法对图像Barbara，Boat进行降噪后，原图像中的噪声几乎全部消去。

(3)图6为局部高斯尺度混合模型的混合傅里叶－小波降噪法、混合傅里叶－小波降噪法、BLSGSM，LAWMAP等方法对图像Barbara进行降噪后的PSNR，与混合傅里叶－小波降噪法、BLS-GSM，LAWMAP等方法相比，本文提出的降噪方法降噪效果显著。

6 结论

本文提出了基于局部高斯尺度混合模型的混合傅里叶－小波降噪法图像进行降噪处理方法，利用局部高斯尺度混合模型充分考虑图像小波变换系数间的相关性，使用协方差替代方差进行小波系数的估计，更加符合现实生活中的数字图像处理。仿真结果表明:

(1)本方法小波函数的选择不影响降噪效果，克服了常规小波变换处理信号时要根据待处理信号的特征选择最合适小波函数的局限性。

(2)采用局部高斯尺度混合模型的混合傅里叶－小波对图像Barbara，Boat进行降噪后，原图像中的噪声几乎全部消去，降噪效果明显。

(3)采用局部高斯尺度混合模型的混合傅里叶－小波降噪法、混合傅里叶－小波降噪法、BLSGSM，LAWMAP等方法对图像Barbara进行降噪后的PSNR结果表明本文采用的方法比上方法的降噪效果有显著提高。

［1］Wu G F，Y He．Application of wavelet thresholddenoisingmodel to infrared spectral signal processing［J］．Spectroscopy and Spectral Analysis，2009，29(12):3246 －3249．

［2］ Jiang S，Hao X．Hybrid fourier-wavelet imagedenoising［J］．Electronics Letters，2007，43(20):1081 －1082．

［3］ Jiang X M，S Mahadevan，H Adeli． Bayesian wavelet packet denoising for structural system identification［J］． Structural Control ＆ Health Monitoring，2007，14 ( 2 ) :333 － 356．

［4］ Rakvongthai Y，A P N Vo，S Oraintara． Complex gaussian scale mixtures of complex wavelet coefficients ［J］． IEEE Transactions on Signal Processing，2010，58 ( 7 ) :3545 － 3556．

［5］ You X G，et al． Image denoising by using nonseparable wavelet filters and two-dimensional principal component analysis［J］． Optical Engineering， 2008， 47( 10) : 107002．

［6］ Fatemi M，H Amindavar，J A Ritcey． Noise reduction via harmonic estimation in gaussian and non-gaussian environments ［J］． Signal Processing，2010，90 ( 5 ) :1554 － 1561．

［7］ Bua desA，B Coll，J M Morel． A review of image denoising algorithms，with a new one［J］． Mu ltiscale Modeling ＆ Simulation， 2005，4( 2) : 490 － 530．

［8］WainwrightM J，E P Simoncelli． Scale mixtures of gaussians and the statistics of natural images， in advances in meural Information processing systems［M］． Cambridge:MIT Press， 2000．

［9］Wang X Y，et al． Image denoising using gaussian scale mixtures with gaussian-hermite PDF in steerable pyramid domain［J］． Journal of Mathematical Imaging and Vision，2011， 39( 3) : 245 － 258．

［10］ GoossensB，A Pizurica，W Philips． Image denoising using mixtures of projected gaussian scale mixtures［J］． IEEE Transactions on Image Processing，2009，18 ( 8 ) :1689 － 1702．

［11］ Guerrero-Colon，J A， et al． Image denoising using mixturesof gaussian scale mixtures［C］． / /15thIEEE InternationalConference on Image Processing，New York． IEEE，2008，( 1 － 5) : 565 － 568．

［12］ Scheunders P，S De Backer． Wavelet denoising of multicomponent images using gaussian scale mixture models and a noise-free image as priors［J］． IEEE Transactions on Image Processing， 2007， 16( 7) : 1865 － 1872．

［13］ Portilla J，et al．Image denoising using scalemixtures of gaussians in the wavelet domain［J］．IEEE Transactions on Image Processing，2003，12(11):1338 －1351．

［14］ Portilla J， et al． Adaptive wiener denoising using a gaussian scale mixture model in the wavelet domain［C］/ /IEEE International Conference on Image Processing． Thessaloniki IEEE， 2001: 37 － 40．