差分法求解吊杆横向振动及在索力检测中的应用

王国红， 盛宏玉

（1.合肥工业大学 土木与水利工程学院，安徽 合肥 230009；2.安徽省建筑设计研究院有限责任公司，安徽 合肥 230002）

吊杆是现代拱桥的主要承载构件之一，吊杆索力的大小直接关系到整桥的受力状况，吊杆索力的控制是保证在服役期内桥梁能够正常工作的关键要素。目前采用频率法测试吊杆的索力主要是基于弦振动理论，导出索力与吊杆自振频率的直接对应关系，再通过检测吊杆的自振频率来推算吊杆的索力。但在实际工程中，基于弦振动理论的频率法与实际情况差别较大，主要原因是弦振动理论忽略了吊杆刚度、边界条件和索体长度等因素对吊杆自振频率的影响。对斜拉桥而言，拉索的长度一般较长，这种影响产生的误差较小，满足工程精度的要求。但吊杆拱桥的吊杆比斜拉桥的拉索要短很多，一般为十几米，有的甚至只有几米，吊杆刚度、边界条件对这种短索自振频率的影响非常大［1－3］。传统的频率法在测量短索的索力时存在较大误差，不能够真实反应短索频率与索力之间关系。因此，需要寻求一种能准确描述索力与频率关系的测试公式。本文综合考虑了吊杆的边界条件、抗弯刚度的影响，采用有限差分法对吊杆的自由振动微分方程进行离散，通过求解特征值问题建立了索力与振动频率的关系；最后结合实验数据进行对比分析，其精度能满足工程要求。

1 吊杆横向自由振动微分方程

目前检测吊杆的索力常采用下列公式：

（1）以弦模型为研究对象，不考虑抗弯刚度EI，计算公式为：

（2）以受轴向拉力的两端简支欧拉梁为研究对象，计算公式为：

其中，FN为吊杆的索力；fn为第n阶自振频率；n为振型阶数；m为单位长度的质量；l为计算长度；EI为抗弯刚度。

通常，吊杆的两端分别采用锚固体与桥体锚固，故两端接近于固支边界条件。由于吊杆一般较短，采用弦模型的（1）式是不合适的，而边界条件对固有频率的影响非常大，故采用测试（2）式也是不合适的。因此，应采用欧拉梁模型，根据实际的边界条件来求解。设梁除了受横向荷载F（x，t）外，还受轴向拉力FN（x，t）的作用，如图1所示。

图1 梁横向振动时受轴向力FN的作用

在梁的轴线x位置处截取单元体dx，根据单元体的受力情况列力和力矩的平衡条件，得到变截面梁受轴向荷载作用和横向荷载共同作用时横向振动的运动微分方程［4］为：

对于等截面梁的自由振动，（3）式变为：

取自由振动解的形式为：

代入自由振动方程（4）式，得

2 两端固支时吊杆的振动频率方程

对吊杆横向振动的微分方程（6）式进行无量纲化处理，取无量纲坐标¯x＝x／l，得

通常，系杆拱桥的吊杆两端锚固于拱肋的顶部和桥面梁板的底面，故一般对方程（7）式采用的两端固支边界条件为：

（7）式为四阶的齐次线性微分方程，根据（8）式和非零解的条件可得等截面吊杆受轴向拉力作用时横向振动的频率方程［5］为：

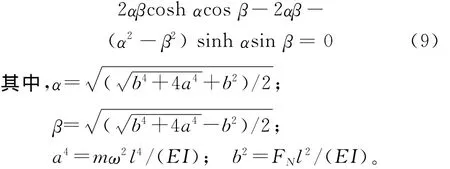
方程（7）和（9）中只包含a和b 2个参量，可方便求解。为找到张力FN与固有频率之间的关系，在求解频率方程（9）时，通常先设定FN的某个值，由吊杆的参数计算对应的b值，再根据数值方法（如频率搜索法）解出一系列的频率参数ai，由此确定对应的各阶固有频率ωi。但频率方程（9）只适合于等截面梁，不适合变截面梁或有附加集中质量（如吊杆两端安装的防雨罩）等情况。为扩大其适用范围，本文应用差分法直接求解方程（7），所得结果将与实验结果及方程（9）的理论解进行对比，以评价求解的有效性。差分法思想简单、适用性强，是一种经济而高效的数值方法。

3 吊杆横向振动微分方程

差分法解题的基本思路是泰勒级数对函数及其导数的逼近。函数f（x）在x0点展开为泰勒级数［6］如下：

对于本文研究的吊杆，在单元划分时将其作为一维问题来考虑。采用中央差分公式，在对方程（7）进行离散时，等间隔将吊杆单元划分为N段，每段的长度h＝1／N，各结点编号依次从0到N，虚设结点的编号为－1和N＋1，如图2所示。

图2 吊杆单元的划分

对第i个结点的差分格式分别为：

根据边界条件Y0＝0，Y′（0）＝0；YN＝0，Y′（N）＝0，可得关系式：

将（11）式代入无量纲方程（7），并考虑边界条件（12）式，对任一结点i可得差分方程为：

结点 1 ［6Y1－4（Y0＋Y2）＋Y1＋Y3］／h4－b2［Y0＋Y2－2Y1］／h2＝a4Y1，即

将以上方程用矩阵表示为：

其中，λ＝a4；A为实对称矩阵；Y 为结点振幅矢量。A、Y分别如下：

采用Matlab编程［7－8］建立方程（15），通过求解特征值问题得出a与b之间的关系，再换算出吊杆的索力与频率之间的关系。为检验差分法求解的有效性，在方程（15）中令b＝1.0，h＝1.0／N，不同的差分网格下频率参数a的计算结果见表1所列。

表1 不同的N时频率参数a的计算结果

由表1可以看出，当N＞100时，差分法的计算结果已收敛，本文取N＝120。

4 吊杆实验及结果的对比分析

为验证本文方法的有效性，设计了吊杆实验，用普通圆钢来模拟吊杆，在材料试验机上对试件施加轴向拉力，用加速度传感器拾取横向振动的响应。为减小传感器附加质量对测试结果的影响，将传感器在靠近试件的端部安装，如图3所示。

图3 吊杆试件及传感器安装图

选择直径d＝10.7mm的圆钢作为吊杆试件的模型，控制最大荷载以保证试件的轴向应力小于材料的屈服极限，弹性模量E＝2.1×105MPa。由于试验机行程的限制，共选择3种长度进行测试。信号采集和频谱分析采用南京安正软件工程有限公司研发的“CRAS动态信号采集与分析系统”，分析得出的典型频谱图如图4所示。频谱曲线中的峰值频率即为吊杆试件的固有频率。各工况下的测试频率与计算频率的结果对比分别见表2所列，其中的误差是指差分解与测试结果的相对误差，理论解由方程（9）求出。

图4 吊杆横向振动的频谱图

表2 吊杆试件固有频率测试结果与计算结果的对比

由表2可见，差分解与理论解的误差非常小，杆件越细越长，差分解与实验结果的误差越小，说明测试误差与试件的长细比λ＝EI／l2有关［9］。另外，二阶频率的误差比一阶频率大。造成测试误差的主要原因如下：① 试件两端并非绝对固支；② 吊杆试件本身的质量不大，传感器附加质量有一定的影响。结果表明，差分法的计算精度能满足工程需要。

5 应用分析

本文引入无量纲的参数，方便了方程的求解与应用。如果给定吊杆的参数与索力FN，可得出无量纲索力参数b，用差分法求解方程（15）可得出一系列无量纲的频率参数ai。限于篇幅，几个不同b值所对应的ai见表3所列，由此即可确定吊杆的固有频率ωi。

而工程检测与上述过程相反，此时吊杆的参数已知，而索力FN待测。应用本文的计算结果，只要将表3中b值的增量取得足够小，就可以根据测试的吊杆固有频率算出对应的a值，通过查表的方式反推出吊杆所对应的b值，进而可确定吊杆的索力FN。

表3 不同b值所对应的频率参数ai

6 结束语

本文运用有限差分法将吊杆的横向自由振动方程转换为特征值方程，采用Matlab软件编程来求解特征值问题，从而求出吊杆的固有频率。差分法具有思想明确、编程方便，同时适合于变截面杆和任意边界条件，因而适用性较广。对吊杆选择不同的截面、长度等几何参数和所受的索力，根据差分法进行参数分析，可以建立索力参数b和频率参数a之间的关系，并能编制详细的数表。在实际工程中，如果吊杆的参数（m，l，EI）已知，可以通过测试的吊杆固有频率确定相应的频率参数a，再来查表确定对应的内力参数b，进而推算吊杆所受的索力。

［1］周先雁，王智丰，冯 新.基于频率法的斜拉索索力测试研究［J］.中南林业科技大学学报，2009，29（2）：102－106.

［2］Russell J C，Lardner T J.Experimental determination of frequencies and tension for elastic cables［J］.Journal of Engineering Mechanics，ASCE，1998，124（10）：1067－1072.

［3］冯仲仁，靳敏超，胡春宇，等.武汉市晴川桥吊杆索力测试分析［J］.武汉理工大学学报，2002，24（12）：49－51.

［4］盛宏玉.结构动力学［M］.第2版，合肥：合肥工业大学出版社，2005：190－207.

［5］克拉夫R W，彭津J.结构动力学［M］.王光远，译.北京：科学出版社，1981：204－207.

［6］徐芝纶.弹性力学简明教程 ［M］.第3版.北京：高等教育出版社，2002：82－85.

［7］苏金明，阮沈勇.MATLAB实用教程［M］.北京：电子工业出版社，2008：40－60.

［8］张 威.MATLAB基础与编程入门［M］.西安：西安电子科技大学出版社，2008：133－172.

［9］郝 翠，王建国，曹新垒.拱塔斜拉桥索塔锚固区应力分析［J］.合肥工业大学学报：自然科学版，2011，34（5）：739－742，747.