基于响应面法的楔横轧非对称轴类件轴向平衡研究
陈乐平,彭文飞,束学道
(1.宁波大学机械工程与力学学院,浙江宁波315211;2.浙江纺织服装学院机电学院,浙江宁波315211)
楔横轧成形技术是一种轴类零件成形新工艺,具有节材显著、生产效率高等优点,在国内外已得到日益广泛的应用[1-4].近年来,随着交通运输业的快速发展,各种轴类零件的需求量与日俱增,如铁路车辆用车轴和汽车半轴等,但是这些零件中大部分为非对称轴类零件.楔横轧非对称轴类零件时,由于轧件外形、尺寸的不对称,如果模具工艺参数选取不合理,将导致轴向力和切向力等不平衡.若不平衡轴向力过大,则会产生轴向窜动,导致台阶缺肉和轧件重皮等缺陷[5-6].因此,保证轧制过程中轴向力的平衡是实现非对称轴类零件楔横轧稳定轧制急需解决的关键问题之一.
响应面法(response surface methodology,RSM)是利用合理的实验设计所获得的实验结果,采用多元二次方程来拟合实验影响因素和响应值之间的函数关系,通过对回归方程的分析来寻求工艺参数对应的结果值,是解决多变量问题的一种统计学方法.本文建立在数值模拟实验的基础上,利用DEFORM-3D软件对典型非对称轴类件的楔横轧轧制过程进行数值模拟,获得不同工艺参数下轴向力的大小.在此基础上,应用Design Expert软件对实验数据进行处理与分析.
1 试验
轴类件楔横轧成形时,轴向力受许多参数的影响,包括成形角α、展宽角β、断面收缩率Ψ、毛坯直径d、轧辊直径D、轧辊转速n和轧制温度T等等.因为实验条件和计算时间的限制,只能考虑其中较为重要的影响参数,而使其他参数保持不变.根据以往的研究经验和文献结果[1,2,7-9],选择轴向力的影响参数中比较重要的4个参数进行研究,即成形角α、展宽角β、断面收缩率Ψ和毛坯直径d.由文献[1]知道,由于受旋转条件、轧件中心疏松及拉伸产生缩颈等的限制,成形角α一般在18°~34°范围内选取,展宽角 β一般在4°~12°范围内选取,而楔横轧一次的断面收缩率Ψ一般应小于75%,但也不能过小,如过小不但轧制尺寸精度不易保证,而且容易出现轧件中心疏松等缺陷,而在楔横轧工艺中得到广泛应用的中小轴类零件其毛坯大小主要集中在20~60 mm范围内.因此在结合理论与实践经验,并考虑中心组合实验设计因素水平的特点后,选取的因素具体水平如表1所示.

表1 因素水平编码表
实验设计方案采用中心组合设计(Central Composite Design,简称CCD),其设计表是在两水平析因设计的基础上加上极值点和中心点构成的,当考虑4个因素水平时,总共有30组实验,具体实验方案如表2所示.

表2 响应面实验方案
2 基于有限元法轴向力的确定
基于DEFORM-3D仿真软件的轴类件楔横轧成形数值模拟结果已得到许多研究人员的验证[7-12],表明用有限元法模拟楔横轧轧制过程,结果可靠,通用性强,且节省实际轧制实验的时间和费用等.因此,本文的实验也建立在有限元仿真基础上.
轴类零件楔横轧成形既有径向压缩和轴向延伸,又存在横向扩展,不但存在材料非线性、几何非线性,而且边界条件也很复杂.在建立有限元分析模型时,只有充分考虑上述多种因素,才能得到成形过程比较真实的描述.根据楔横轧变形特点,作如下假设[13,14]:
1)由于轧制是在高温下进行,轧辊的弹性变形比轧件的塑性变形小很多,可忽略轧辊的弹性变形与模具局部压扁变形,将轧辊、模具和导板视为刚体;
2)轧件视为刚塑性体,并忽略其自重;
3)由于整个轧制过程是在很短时间内完成,轧制时轧件与模具和空气间的热传递时间很短,可以认为轧件在轧制过程中温度保持恒定;
4)将轧辊与轧件间的摩擦简化为剪切摩擦.
如果将轧件整体进行模拟,得到的轴向力是轧件左右两端总轴向力之和,因此将轧件从中间剖开,作如图1所示的轴向几何约束处理.最后根据轧件轧制过程建立的有限元模型如图2所示,模型中轧件材料为45#钢,弹性模量E为90GPa,泊松比为0.3,轧辊直径为620mm,轧制温度为1050℃.

图1 轴向几何约束
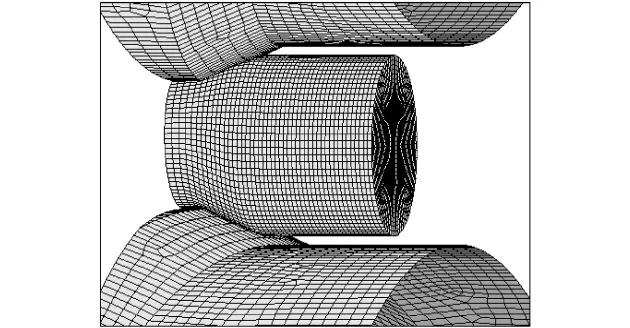
图2 有限元模型
结合实验设计方案,通过DEFORM-3D软件的模拟仿真,获得实验方案对应的楔横轧轧制过程的轴向力如表3所示.
3 结果分析与验证
利用Design Expert数据分析软件进行回归分析,得到的方差分析结果如表4所示.
由表4可知,成形角α、展宽角β、断面收缩率Ψ和毛坯直径d的一次项达到极显著水平(p<0.01),表明这4个因素对轴类件楔横轧成形时轴向力的线性效应显著,断面收缩率Ψ、毛坯直径d的二次项对轴向力的曲面效应显著;同时,αΨ、αd、βΨ的交互效应显著(p<0.05),表明各影响因素对轴向力的影响不是简单的线性关系,而有较强的非线性效应.从表4的分析结果来看,整体模型的p<0.0001,说明该二次方程模型达到极显著水平,表明该回归方程对模拟仿真实验数据进行了较好拟合,二次回归方程为:
R=23926.25698-1014.14325×α-591.54903×β-129.72885×Ψ-513.62581×d+26.03283×α×β+4.96367×α ×Ψ+15.71088×α ×d+10.19638×β×Ψ-15.57979×β×d+3.85412×Ψ×d+4.78865×α2-19.11764×β2-1.44433×Ψ2+5.62388×d2

表3 仿真计算结果
为验证回归模型的正确性,采用文献[15]在钢球实验轧机上所做的第1号实验,具体轧制工艺参数如表5所示.在实际轧制过程中,因考虑到工件从加热炉转移到实验轧机的过程中有散热,故出炉温度选择为1125℃,稍高于数值仿真模型的轧制温度1050℃.

表4 回归模型方差分析
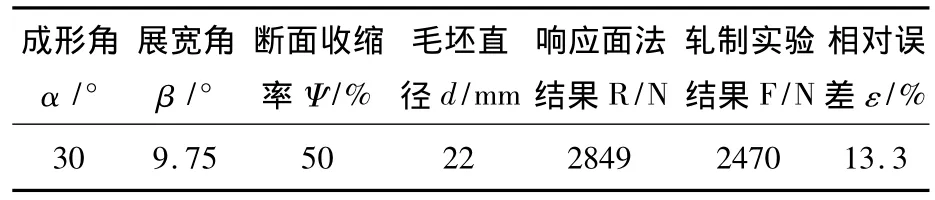
表5 模型的实验验证
由表5可以看到,响应面法计算结果和实际轧制实验结果误差为13.3%,说明此模型的拟合程度良好,实验误差小,从统计学上是可行的,能很好的近似轴类件楔横轧成形过程中的轴向力.
4 基于响应曲面的楔横轧非对称轴类件轴向平衡
非对称轴类件楔横轧成形时,要保证轧制的稳定进行而不出现轴向窜动,就必须保证轧件左右两端的轴向力相等,但由前面的分析可知,包括成形角α、展宽角β、断面收缩率Ψ、毛坯直径d等因素都对轴向力有重要影响,而且各因素对轴向力的影响不是简单的线性关系,有较强的非线性耦合,这给非对称轴类件楔横轧成形的工艺参数选择提出了极大的挑战.目前都是通过多次数值仿真及修模以改变模具的工艺参数来达到两端轴向力相等或近似相等,这种方法繁琐、费力,而且如果模具初始参数选择不好,即使后期多次修模也可能无法达到轴向力的平衡而造成模具报废.本文通过利用响应面法的等值线进行工艺参数选择,却能够保证轧制成形的轴向力相等或近似相等,从而保证非对称轴类件楔横轧的稳定进行.
以图3的非对称轴类件为例,说明响应曲面法的具体应用.首先毛坯直径是不能选择的,一般为零件最大外径,本例为35mm,为了保证楔横轧的轴向平衡,左右两端的轧制展宽段应大致同时开始和结束,因此选择相同的展宽角7°,在毛坯直径和展宽角确定的情况下,得到轴向力的响应曲面及等值线图如图4所示.
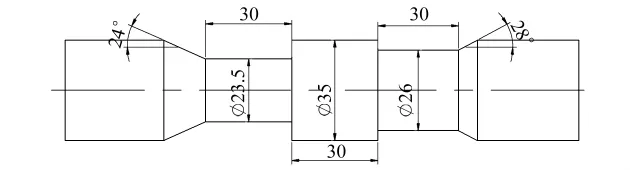
图3 非对称轴类件
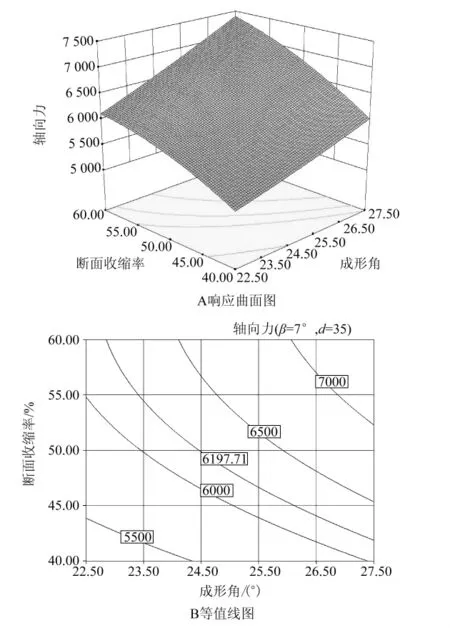
图4 轴向力响应曲面及等值线图
由图4可以看到,为了保证轴向平衡,只需要左右两端所选择的成形角及断面收缩率的交点位于同一条等值线上,即能保证非对称轴类件楔横轧的轴向力相等,以此非对称轴类件为例,可以选择左端参数为断面收缩率55%和成形角22.5°,而右端断面收缩率为45%和成形角为25°,则能近似保证两端轴向力均为6000N左右,从而满足轴向平衡.
实际工程中,针对一个特定的楔横轧产品而言,毛坯直径和断面收缩率是确定的,不能随意调整,且断面收缩率左右两端通常不会一致,这就意味着不能利用一张等值线图来选择工艺参数,但可以通过两张基于不同工艺参数的等值线图,如图5所示,A、B两图即基于不同的断面收缩率.利用响应面法,可以任意选取其中2个工艺参数的值,然后绘出另外2个工艺参数下轴向力的等值线图,以辅助非对称轴类件楔横轧工艺参数的选择.具体为首先分别根据左端和右端的毛坯直径和断面收缩率获得成形角和展宽角对应的轴向力等值线图,然后只要保证左、右两端成形角及展宽角的交点位于同一等值线,就自然满足非对称轴类件楔横轧轴向力的平衡.
以图3非对称轴类件为例,图5.A为断面收缩率55%和毛坯直径为35mm时展宽角和成形角对应的轴向力等值线图,而图5.B为断面收缩率45%和毛坯直径为35mm时展宽角和成形角对应的轴向力等值线图,要保证楔横轧成形时的轴向平衡,只需左、右两端工艺参数的选择相交于相同等值线即可,如选取轴向力为6500N的等值线,则左端工艺参数可选取为展宽角7°和成形角25°,而右端的工艺参数也必须在6500N等值线上选取,可以选择展宽角6°和成形角26.5°或其它6500N等值线上的组合,则基本保证了非对称轴类件楔横轧的轴向平衡.

图5 不同断面收缩率下的轴向力等值线图
5 结论
采用中心组合实验设计,结合响应面法分析,利用响应曲面和等值线图辅助非对称轴类件楔横轧成形时轧制工艺参数的选择,实现左、右两端的轴向力平衡,保证轧制过程的稳定进行.此方法简单、直观、便捷,无需大规模繁琐的计算与试模,极大地缩短了楔横轧模具的设计周期并节省经济成本,为推广楔横轧技术在非对称轴类件上的应用提供新的技术与方法.
[1]胡正寰,张康生,王宝雨,等.楔横轧零件成形技术与模拟仿真[M].北京:冶金工业出版社,2004.
[2]胡正寰,张康生,王宝雨.楔横轧理论与应用[M].北京:冶金出版社,1996.
[3]杨翠苹,胡正寰,张康生,等.楔横轧轧件轴向变形研究[J].机械工程学报.2004,40(9):80-83.
[4]PATER Z.A study of cross wedge rolling process[J].Journal of Materials Processing Technology,1998,80-81:370-375.
[5]沈智.大直径楔横轧件的成形工艺研究[D].北京:机械科学研究总院,2006.
[6]李建国.楔横轧轧件扭转变形规律的研究[D].北京:北京科技大学,2007.
[7]束学道,邢希东,李连鹏,等.楔横轧轧制力矩变化规律的实验研究[J].冶金设备,2005,(4):1-3,6.
[8]束学道,胡正寰,李连鹏,等.楔横轧轧制力矩规律有限元分析与实验测试[J].中国机械工程,2006,17(9):962-965.
[9]束学道,张康生,胡正寰,等.楔横轧力能参数影响因素分析[J].重型机械,2002,(4):29-33.
[10]束学道,邢希东,胡正寰等.工艺参数对楔横轧多楔轧制成形机理影响分析[J].北京科技大学学报,2005,27(2):222-226.
[11]束学道,彭文飞,聂广占,等.楔横轧大型轴类件轧制力规律研究[J].塑性工程学报,2009,16(1):102-105,114.
[12]束学道,邢希东,胡正寰,等.基于有限元法分析的楔横轧多楔轧制力能参数规律[J].重型机械,2004,(6):19-21,34.
[13]SHU Xue-dao,LI Chuan-min,Hu Zheng-huan.Theoretical and experimental study of varying rule of rolling-moment about cross-wedge rolling[J].Journal of Materials Processing Technology,2007,187:752-756.
[14]彭文飞,张康生,贾 震,等.楔横轧非对称轴类件有限元模型分析[J].塑性工程学报,2010,17(2):79-83.
[15]张卫国.楔横轧空间力参数研究[D].北京:北京科技大学,1985.

