基于合作目标与非合作目标的一体化空间配准新算法*
宋文彬
(中国西南电子技术研究所,成都610036)
1 引言
空间配准指利用多传感器对空间共同目标的量测对各系统偏差进行估计和补偿[1]。空间配准技术主要包括基于合作目标的空间配准和基于非合作目标的空间配准两类[2],其中合作目标指被探测目标的真实位置信息除了传感器直接量测外还可以通过其他合作渠道获得,如某个固定目标的位置是事先已知的,或友机通过无线电不断报告其自身精确的导航位置等;非合作目标指除传感器探测以外,再无任何其他手段能够获取目标的准确位置,如来袭导弹、敌机等。对于前者,往往只需要一个平台和一个合作目标即可,将其他渠道获得的目标位置经坐标变换至传感器量测坐标系下,再分析与传感器真实量测的差值情况;对于后者,则需要至少两个平台,它也是目前空间配准研究的主要功能所在,如刘煜等人[3]提出修正传感器定姿偏差的空间配准算法;Helmick和Rice[4]利用标准卡尔曼滤波方法估计传感器量测系统偏差及所在平台的姿态偏差;Karmiely和Hava[5]首次运用神经网络方法来估计传感器系统偏差;王建卫[6]把系统偏差估计问题转化为非线性优化问题,通过模拟退火算法求解系统偏差;胡雷等[7]提出了一种在地心地固坐标系下操作的约束总体最小二乘空间配准算法;赵杰等人[8]提出了多无源传感器在线空间配准算法,其先由传感器量测的多个角度数据反演目标距离,再依据估计距离初始化滤波器,从而实现对传感器角度偏差的配准。文献[9]中提出了差异维度传感器数据融合方法,但此方面的空间配准研究尚未见报道。本文研究的是当同时出现合作目标与非合作目标时,怎样协调好基于合作目标的空间配准结果与非合作目标信息,共同提高有合作目标一方及无合作目标一方量测航迹的配准精度。
2 一体化空间配准算法
在介绍具体方法前,先介绍基于非合作目标的空间配准算法,因为一体化空间配准算法是在它的基础上改造完成的。非合作目标空间配准算法的原理是先将ECEF直角坐标系下A、B两平台所有关联目标的雷达量测航迹两两相减,消去目标真实位置向量,而仅剩下雷达观测误差向量之差。然后利用多拍的误差向量差值,递推地估出平台A、B雷达量测系统偏差的大小。最后将估出的系统偏差在目标量测航迹中进行扣除。下面给出综合系统偏差估计的具体步骤。
(1)方程建立
扣除系统偏差后A、B两平台上的雷达量测航迹在ECEF坐标系下应完全重合。令参数
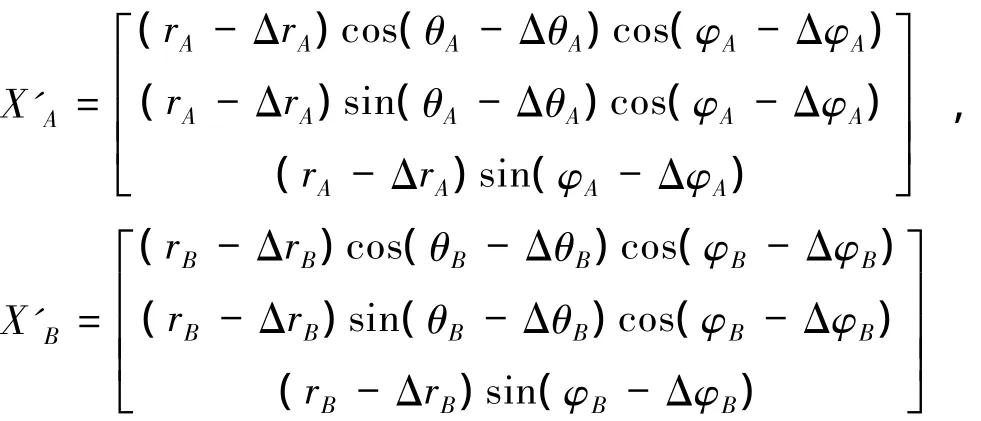
其中,r、θ、φ 为雷达量测距离、方位角和俯仰角,Δr、Δθ、Δφ为相应的综合系统偏差。构建方程
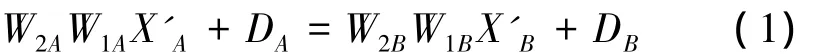
其中,W1为移动平台直角坐标系转至其地理坐标系的转移矩阵,W2为移动平台地理坐标系转至ECEF坐标系的转移矩阵,D为平台在ECEF坐标系下的三维坐标。
(2)方程线性化
利用泰勒多项式展开,将待估参数Δr、Δθ、Δφ分离出来,可得雅可比矩阵
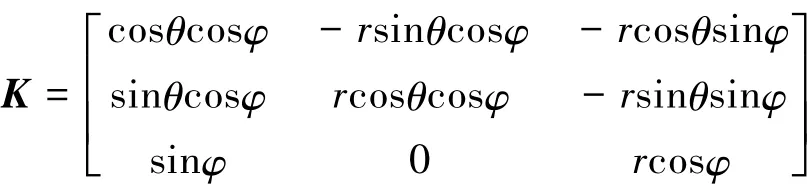
于是原方程变更为线性方程
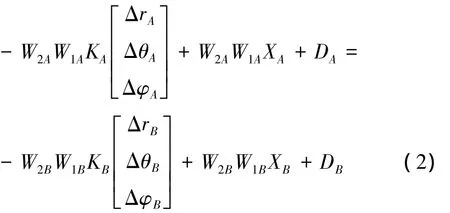
其中:
均为已知观测量。
(3)方程求解
采用最小二乘法来实时估计雷达量测系统偏差大小。假定平台A和平台B总共量测了N拍,则可建立N个类似公式(3)的方程

其中:
对于上述方程,其最小二乘解为
一体化空间配准算法解决的是同时存在合作目标和非合作目标的情形,尤其是在进行基于非合作目标空间配准时,突然某平台的雷达发现了合作目标,比如僚机突前作战刚好被后方长机雷达捕捉到,僚机又通过机间链向长机不断报告自身位置,从而成为了合作目标。这里假定平台A看到了合作目标,并利用合作目标空间配准算法[10]每拍可实时估出 ΔA的大小,令作 ΔA(1),…,ΔA(N),此时更改公式(4)的系数为
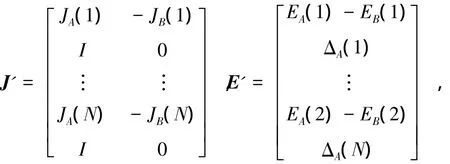
其中,I为3×3的单位矩阵,新条件下两平台雷达量测系统偏差的最小二乘估计结果为
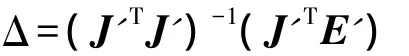
3 仿真分析
图1给出了所用仿真场景的目标航迹,(a)为在水平面内的投影,其中左边两架飞机上面的为僚机,下面的为长机,均朝右方飞行,僚机充任长机的合作目标;右侧为3架敌机,由上至下编号依次为1#、2#和3#,均朝左方飞行,能被我方长机和僚机的雷达同时探测到;其中黑色的为长机量测航迹,灰色的为僚机量测航迹,浅灰色的为目标真实航迹;(b)为长僚机平台和3架敌机的立体航迹,三坐标轴分别表示经度、纬度和高度,左下方的灰色航迹为僚机导航给出的自身位置,灰色航迹上方是长机雷达量测的僚机航迹;僚机航迹右上方较近的黑色航迹为长机导航给出的自身位置,其余为3架敌机的真实航迹及长僚机雷达对它们的量测航迹,可见因为系统偏差的存在,量测航迹已显著偏离了目标真实航迹。表1则列出了仿真场景所用的各物理量参数随机误差和系统偏差的大小,其中平台姿态与雷达量测随机误差与当前设备性能处在同一个数量级水平,系统偏差也是如此。为了说明算法的通用性,我们有意将系统偏差符号设为相同,这样两雷达量测航迹将朝同一个方向偏移,如图1所示,后面可以发现经空间配准后它们的整体偏移都得到了一定程度的校正。
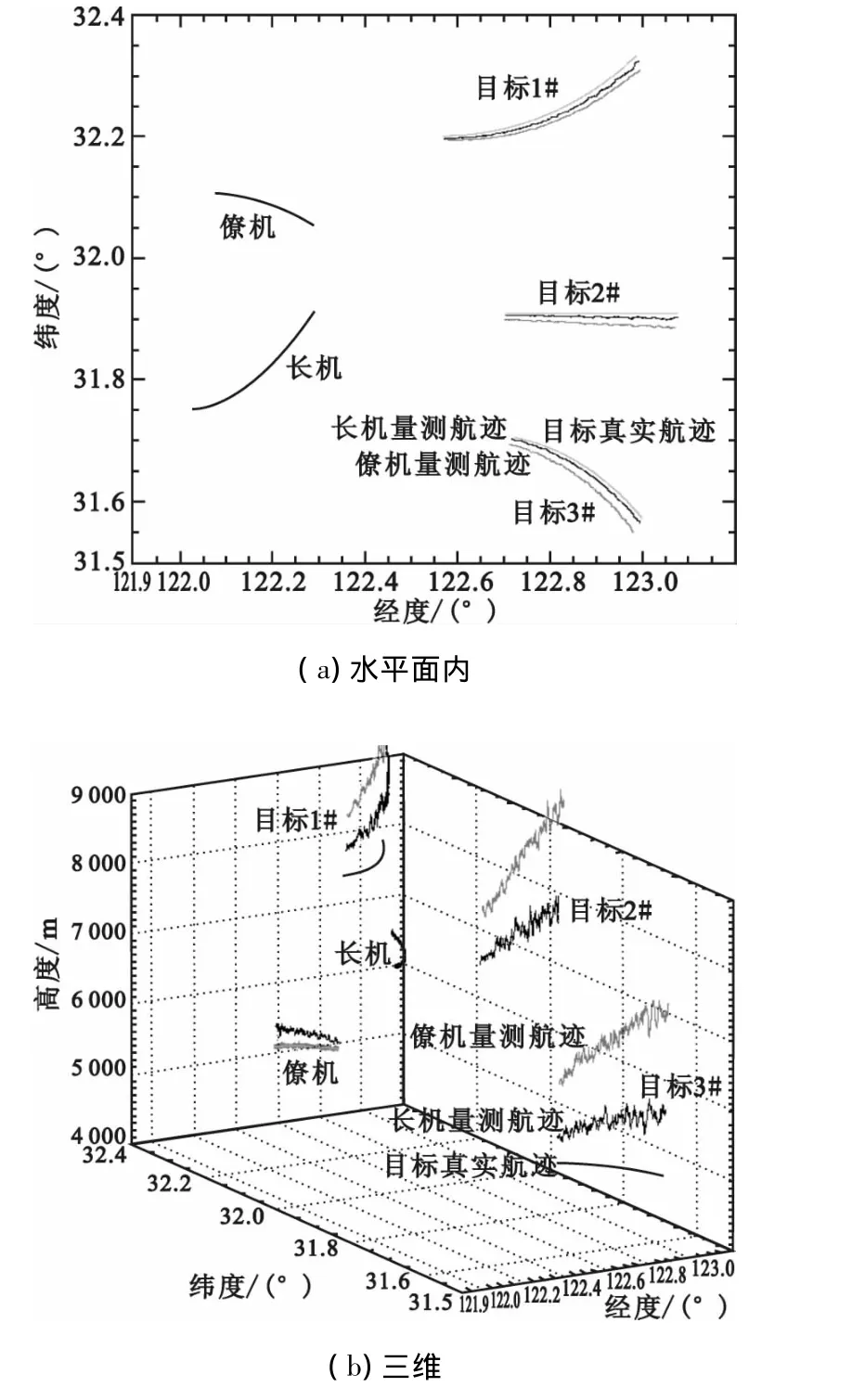
图1 机载雷达量测目标航迹仿真场景Fig.1 The simulative scene of the measured targets'tracks
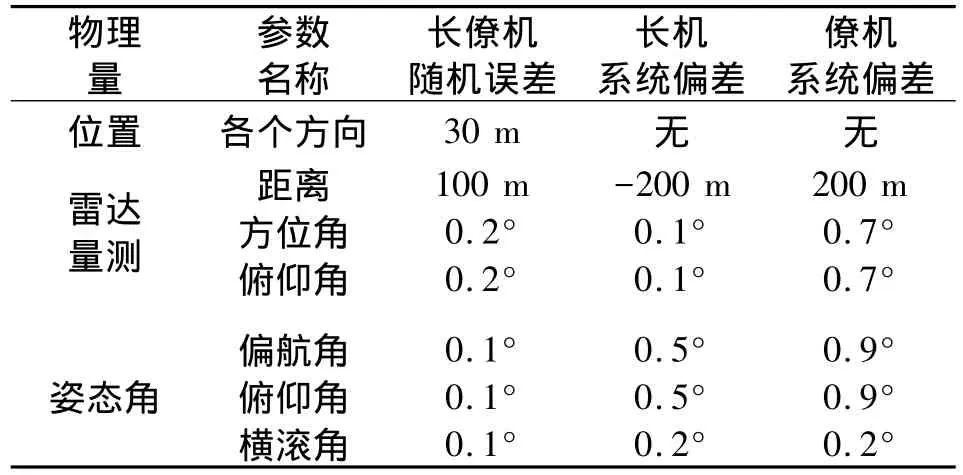
表1 雷达量测与飞机导航误差大小设置Table 1 The measurement errors of airborne radars and navigational outputs
图2给出了基于合作目标与非合作目标一体化方法的长僚机综合系统偏差估计结果,(a)为长机系统偏差估计,(b)为僚机系统偏差估计,从上至下依次为距离、方位角和俯仰角系统偏差,上排水平的虚线为想定预设的雷达距离系统偏差值,中排的虚线为想定预设的雷达方位角系统偏差与平台姿态偏航角系统偏差之和。可以发现,因平台姿态不存在距离项,故估出的综合距离系统偏差值非常接近于雷达预设的距离系统偏差值。对于方位角综合系统偏差,当平台做平飞运动时,即姿态俯仰角和横滚角均为0,雷达量测方位角系统偏差和平台姿态偏航角系统偏差是完全耦合在一起的,估出的综合方位角系统偏差值应等于它们的和。图中方位角综合系统偏差的估计值与虚线基本吻合正好印证了耦合的判断。对于俯仰角综合系统偏差,其等于雷达量测俯仰角系统偏差与平台姿态俯仰角系统偏差之和,也即完全耦合,除了需要平台平飞的条件之外,还要求目标所在方位角为0,即位于平台正前方。故显然不满足条件,估出来的俯仰角综合系统偏差既不等于雷达量测俯仰角系统偏差,也不等于平台姿态俯仰角系统偏差,同时还不等于这两者之和。另外,图中可见长僚机综合系统偏差估计的时变起伏很小,非常接近于一条水平直线,说明算法的偏差估计性能比较稳定。
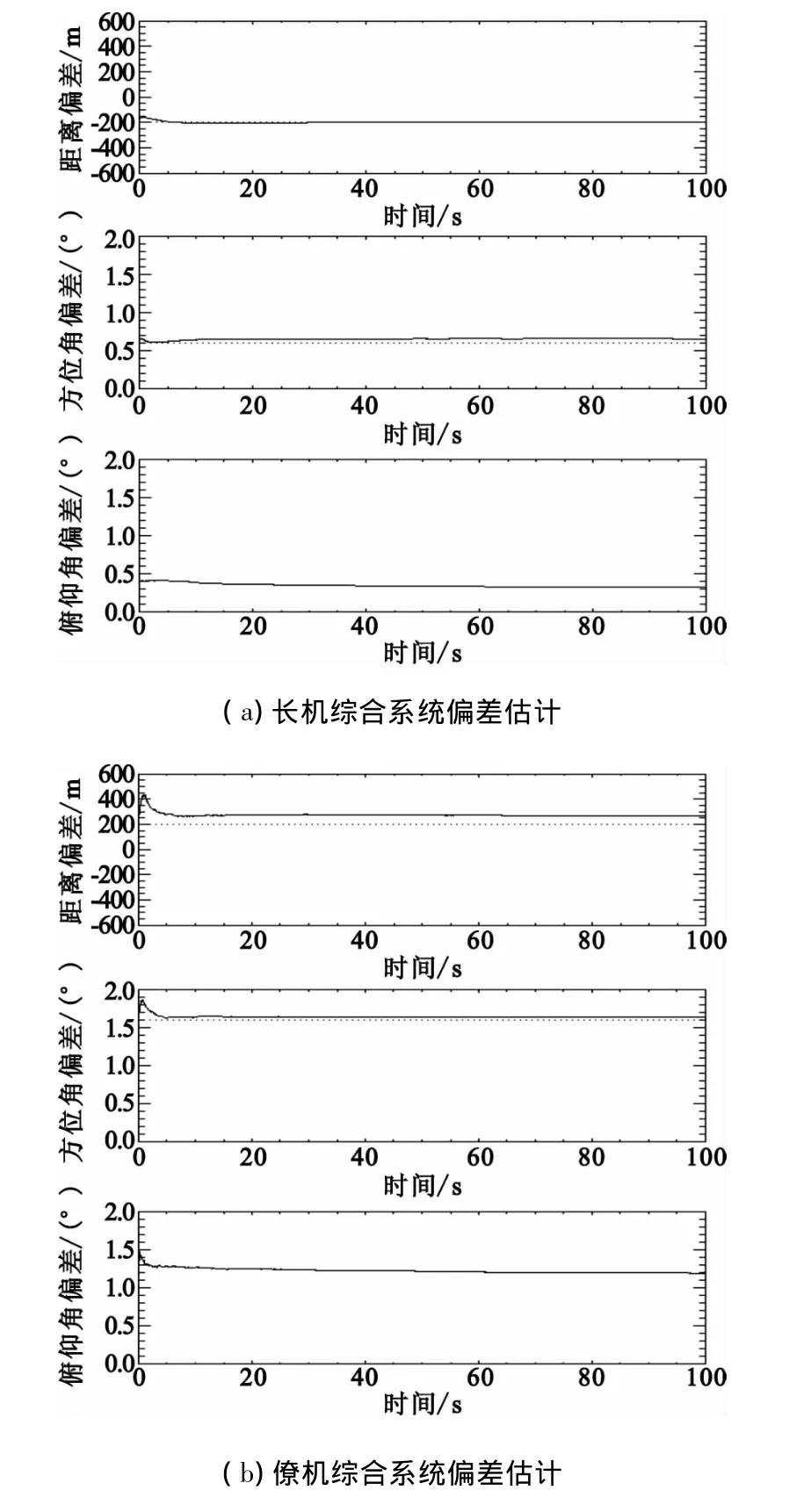
图2 长机综合系统偏差估计与僚机综合系统偏差估计Fig.2 The bias estimation of radar measurements of the leading plane and the wing plane
为了进行比对,突出合作目标对非合作目标空间配准的支撑作用,图3(a)给出了仅使用3个非合作目标进行空间配准得到的长僚机雷达量测目标航迹,图3(b)给出了基于合作目标与非合作目标一体化空间配准后的长僚机雷达量测目标航迹,可见配准后的目标航迹较图3(a)在高度维效果明显好很多。表2则列出了航迹配准前后详细的经纬高偏移量统计结果,从中可以看出在水平方向一体化空间配准效果(见配准后列每个编号栏的下方)是好于纯非合作目标空间配准效果(见配准后列每个编号栏的上方)的。对于纯非合作目标的空间配准,长机对1#目标的量测航迹高度差从777 m下降到了338 m,但对2#和3#目标没有什么改善;僚机对3架敌机的量测航迹高度差则均从1600 m以上下降到了800 m以下,效果还是较好的;而对于一体化空间配准后的航迹,其最大高度偏差低于400 m。

图3 基于非合作目标的空间配准航迹与基于一体化目标的空间配准航迹Fig.3 Targets'tracks after space registration processing based on noncooperative targets and incorporation targets
另外,表2还定量统计了两种配准方法前后目标量测航迹偏离目标真实航迹的距离比,相关公式如下:
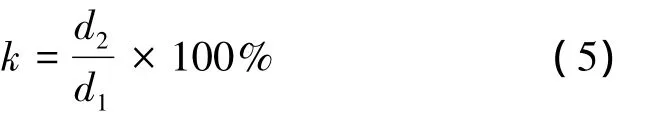
其中,d1表示配准前航迹的偏移距离,d2表示配准后的航迹偏移距离。从表2最后一列情况看,一体化空间配准后目标航迹偏差均有明显改善,效果差点的能到30%左右,效果好点的能到5%。这主要是因为长机多了合作目标信息,相当于知道了ΔA的答案,只需估计ΔB的大小,未知数由6个一下子变成了3个,所以一体化配准的性能可以显著改善。
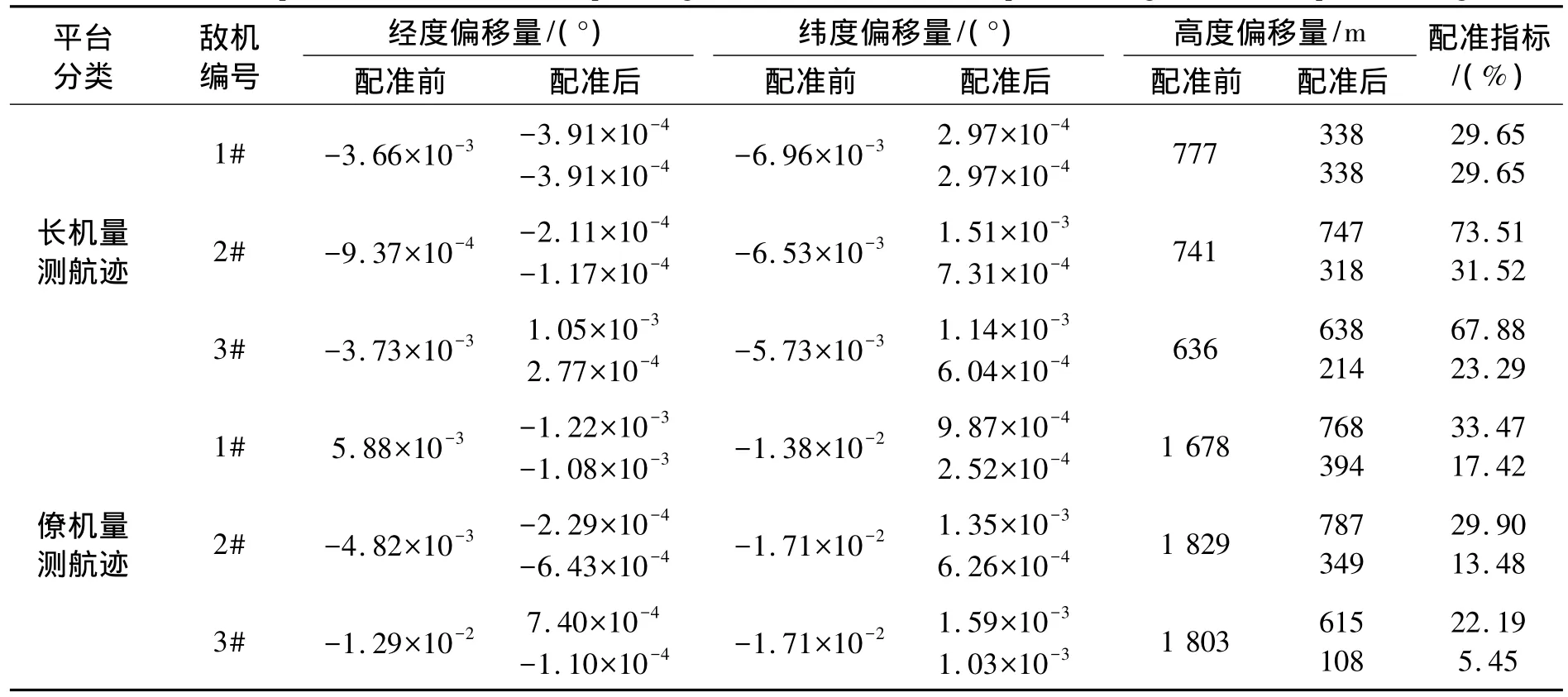
表2 基于非合作目标的与基于一体化的空间配准结果比较Table 2 The comparison of the results of space registration based on noncooperative targets and incorporation targets
4 结论
本文研究了基于合作目标与非合作目标的一体化空间配准算法,在双移动平台基于非合作目标空间配准算法的基础上,增加单平台基于合作目标的系统偏差估计信息,并将这些信息作为新的3个线性方程加入到原利用共同的非合作目标建立的线性方程组中,综合在一起采用递推最小二乘法估计两平台的综合系统偏差大小。为了检验该新方法,设计了2对3的空战仿真场景,其中我方僚机充当了长机的合作目标,它们又同时探测到了3架敌机。仿真结果表明提出的方法效果很好,主要表现在:
(1)合理地利用了长机基于合作目标的估计结果,对长机的综合系统偏差进行了重新估计,精度和稳定性都有了明显改善;
(2)与基于纯非合作目标的空间配准效果相比较,收敛性能更好,航迹精度改善更加明显,不但改善了长机的量测航迹,同时也间接地改善了僚机的量测航迹。
在实际应用中,一般合作目标的出现具有临时性和偶然性,所以该算法需要跟基于非合作目标的空间配准算法进行联合设计,实现无缝切换,基于两种方法的航迹配准结果前后紧密衔接,以满足目标持续跟踪的需要。
[1]韩崇昭,朱洪艳,段战胜.多源信息融合[M].北京:清华大学出版社,2006.HAN Chong-zhao,ZHU Hong-yan,DUAN Zhansheng.Multi-source information fusion(Vol.II)[M].Beijing:Tsinghua University Press,2006.(in Chinese)
[2]宋文彬.传感器数据空间配准算法研究进展[J].传感器与微系统,2012(8):5-8.SONG Wen-bin.Research progress of spatial registration algorithms for sensor data[J].Transducer and Microsystem Technologies,2012(8):5-8.(in Chinese)
[3]刘煜,杨哲,韩崇昭.传感器定姿偏差的空间配准算法研究[J].现代雷达,2009,31(2):29-31.LIU Yu,YANG Zhe,HAN Chong-zhao.A study on space registration algorithm of sensor attitude bias[J].Modern Radar,2009,31(2):29-31.(in Chinese)
[4]Helmick R E,Rice T R.Removal of alignment errors in an integrated system of two 3D sensors[J].IEEE Transactions on Aerospace and Electronic Systems,1993,29(10):1333-1343.
[5]Karmiely H,Hava T S.Sensor registration using neural network[J].IEEE Transactions on Aerospace and Electronic Systems,2000,36(1):85-100.
[6]王建卫.基于模拟退火算法的组网雷达系统误差校正[J].现代雷达,2006,28(8):4-8.WANG Jian-wei.Multiple sensor registration using simulated annealing algorithm[J].Modern Radar,2006,28(8):4-8.(in Chinese)
[7]胡雷,林岳松,郭云飞.约束总体最小二乘空间配准算法[J].火力指挥控制,2011,36(10):5-8.HU Lei,LIN YUE-Song,GUO Yun-fei.Space registration algorithm based on constrictive total least squares[J].Fire Control& Command Control,2011,36(10):5-8.(in Chinese)
[8]赵杰,江晶,周祥晶,等.基于序贯最小二乘的多传感器误差配准方法[J].传感器与微系统,2007,26(8):99-201.ZHAO Jie,JIANG Jing,ZHOU Xiang-jing,et al.RLS-based registration algorithm for multi-sensors[J].Transducer and Microsystem Technologies,2007,26(8):99-201.(in Chinese)
[9]宋文彬.差异维度传感器数据融合新方法[J].电讯技术,2013,43(3):28-32.SONG Wen-bin.A new data fusion algorithm for sensor measurements of different dimensions[J].Telecommunication Engineering,2013,43(3):28-32.(in Chinese)
[10]董云龙,车志宇,何友,等.一种基于固定目标进行误差配准的方法[J].弹箭与制导学报,2004(4):380-382.DONG Yun-long,CHE Zhi-yu,HE You,et al.A registration method using static target[J].Journal of Projectiles Rockets Missiles and Guidance,2004(4):380-382.(in Chinese)

