蔡氏混沌电路在Multisim软件中的设计与仿真

(盐城师范学院物理科学与电子技术学院，江苏盐城224001)

(盐城师范学院物理科学与电子技术学院，江苏盐城224001)

经典的蔡氏电路是一个简单混沌电路，能够产生丰富的混沌现象，然而该电路的系统参数基本上是固定的，不同混沌电路之间的电路不具备通用性。基于此，提出在Multisim软件上通过模块化的设计方法重构蔡氏混沌电路，所有电路参数均独立可调，着重介绍了如何用二极管及运算放大器实现复杂的非线性函数，并给出了蔡氏混沌电路相应的双涡卷吸引子仿真结果。

蔡氏混沌电路;模块化设计;Multisim仿真;鞍焦点;绝对值电路

众所周知，典型的蔡氏电路［1］仅仅通过对一个电阻的调节，便可从电路中观察到周期极限环、单涡旋和双涡旋混沌吸引子的非线性物理现象。为能够使蔡氏电路具有通用性的特点，在对蔡氏电路分析的基础上，利用反相加法电路、反相积分电路和反相器电路可实现对所有参数的控制调整。

1 蔡氏混沌系统及MALAB仿真

1.1 典型的蔡氏混沌系统

蔡氏电路如图1(a)所示，它是由一个线性电感、两个线性电容、一个线性电阻和一个非线性电阻构成的三阶自治动态电路，非线性电阻的伏安特性iN=g(vN)，是一个分段线性函数。电路中电感L和电容C2构成了一个LC振荡电路，有源非线性电阻RN(蔡氏二极管)和电容C1组成了一个有源RC滤波电路，它们通过一个电阻R线性耦合，形成了只有5个元件即能产生复杂混沌现象的非线性电路。

设电容电压uC1，uC2和电感电流iL为状态变量，得电路的状态方程［2］如下:

1.2 蔡氏混沌系统的理论分析

令式(1)中x=v1，y=v2，z=iL，对C1，C2，L及R0等取一组定值可以得到如下所示的蔡氏系统状态方程［3］。

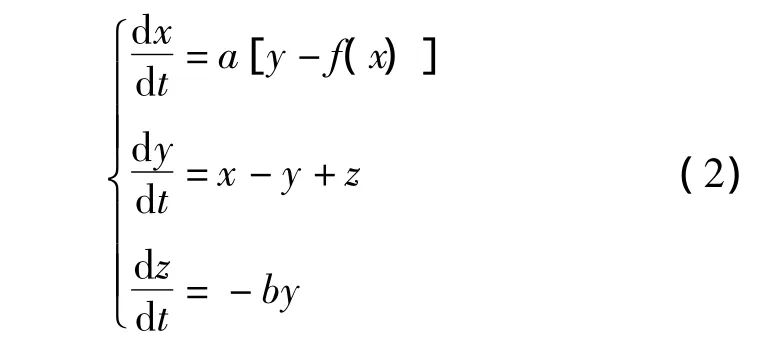
为了能够计算出系统平衡点处的数值，考虑到该系统中惟一的非线性函数f(x)是分段线性函数，故f (x)可以表示成如下形式:

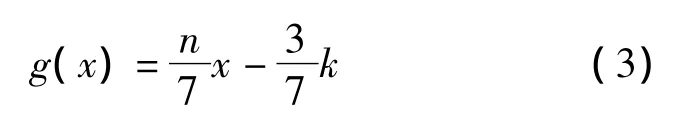
再由各线性区域的平衡点处方程计算出平衡点数值，其结果如表1所示。

表1 Chua系统的平衡点

由该Chua系统的状态方程，根据系统平衡点处的Jacobin矩阵［1］计算其对应的特征值为:

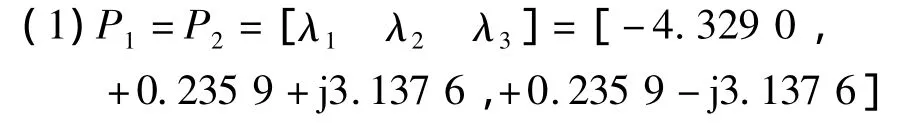
故在此处平衡点形成的是两个相同的指标为2的鞍焦点。

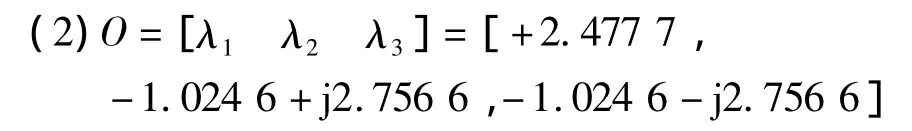
故在此处平衡点形成的是一个指标为1的鞍焦点。

根据混沌系统存在的条件［3］，很显然蔡氏系统存在2个指标为2的鞍焦点，1个指标为1的鞍焦点，因此最多只能产生双涡卷的混沌吸引子。

1.3 蔡氏电路的MATLAB仿真

根据统一的蔡氏电路状态方程，利用MATLAB数值仿真软件对其进行仿真可以得到系统的时域波形图和相图，充分说明变换后的系统与原系统是一致的。

2 蔡氏电路Multisim硬件仿真

2.1 Chua状态方程的通用模块化电路设计

2.1.1 非线性电路的设计

通用模块化混沌［4-5］电路设计的基本思想是使用运算放大器、电阻、电容、二极管等电子元件构成基本的运算放大电路。本论文主要用到反相加法器、反相积分器、反相器和绝对值电路。

图2 x方向时域波形图

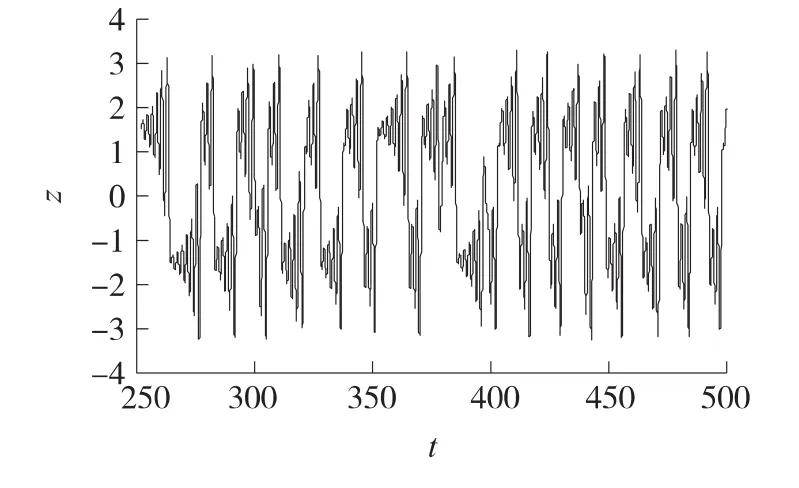
图3 z方向时域波形图

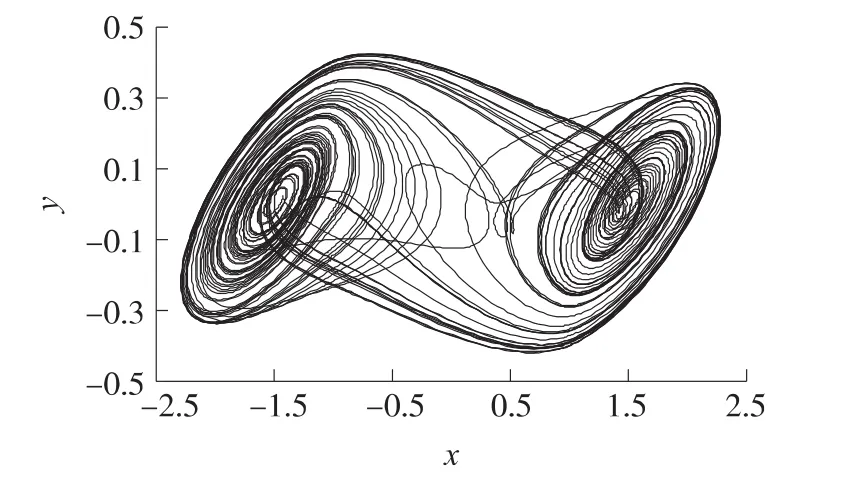
图4 x-y相平面图

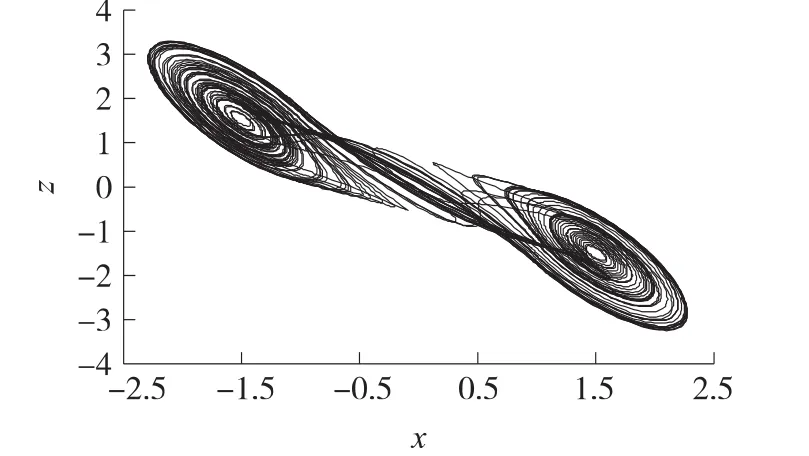
图5 x-z相平面图

(1)反相加法运算电路 反相加法运算电路如图6所示，其运算关系式为:

式中R/Rn为比例系数，在反相加法电路中，只要选取适当的电阻R值固定，再分别独立调整电阻Rn，即可得到反相加法的各系数。

(2)反相器电路 反相器电路是反相加法电路的一种特殊形式，若R=R1，将图6的x2，x3，…，xn输入信号接地或断开按键KEY1，即可构成反相器电路，其运算关系式为:

图6 反相加法比例运算电路

(3)反相积分器 微分电路是由多阶微分方程构成混沌电路的关键，考虑到微分电路对实际的电路信号会产生跃变，信号容易产生畸变，故将微分方程转换为积分形式，其中式(6)中的τ=RC为积分时间常数，一般取R为10 kΩ～50 kΩ，C取33 nF，如图7所示，其运算关系式为:

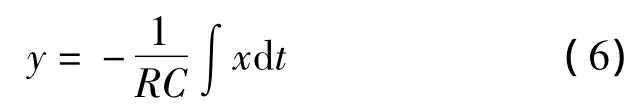
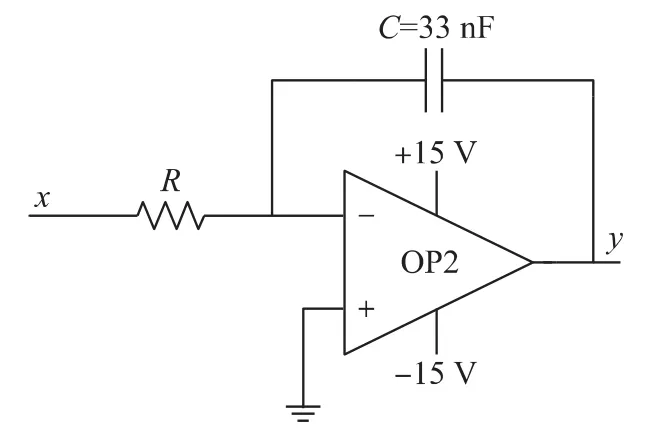
图7 反相积分器

(4)绝对值电路 一种常见的绝对值电路如图8所示，R4=20 kΩ，R1=R2=R3=10 kΩ，电阻R2和电阻R3之间的电压为u1，则根据叠加原理得，即u0=2(u-u1)+u。①若u＜0，二极管VD1、VD2截止，OP1运放输入端虚短，电压为u，故，即u1=2u，得u0=-u＞0。②若u＞0，VD1导通，VD2导通，故u1=u，得u0=u＞0。由①②可知u0=|u|。

图8 绝对值电路

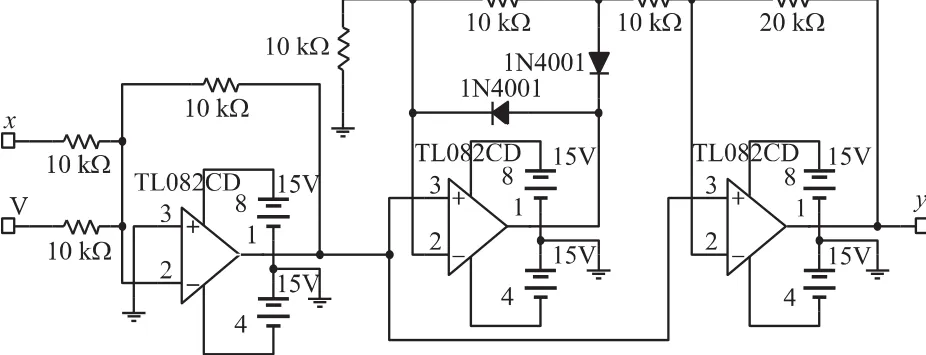
图9 |x+1|电路图

其中1 V输入信号和x，经过反相加法运算电路得到输出信号-(x+1)，再经过绝对值电路即得到输出y1=|x+1|。

在此基础上，将输入信号x经过反相器得到输出信号-x，它和1 V输入信号经过反相加法运算电路得到输出信号 x-1，再经过绝对值电路得到|x-1|，其经过反相器即得到y2=-|x-1|，图10所示为-|x-1|的电路图。

图10 -|x-1|电路图

根据得到的|x+1|、-|x-1|电路，利用反相器电路、反相加法电路可以实现基于蔡氏混沌电路的f(x) =［|x+1|-|x-1|］非线性电路图，如图11所示。

图11 f(x)的电路设计图

其中输入信号x经过反相器得到的输出信号-x与输入信号y1，y2一起经过反相加法比例运算电路得到非线性函数f(x):

2.1.2 Chua状态方程的电路设计

由Chua系统的状态方程式(2)，将其三阶微分方程转换为积分形式，即:

(1)根据式(8)得可以得到输出为x的电路图，如图12所示。

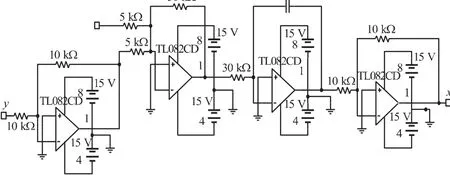
图12 x的电路设计图

图12中输入信号y经过反相器得到的信号-y与输入信号f经过反相加运算电路得到10(y-f)，它通过反相积分器得到 -x，再经过反相器即得到x。

(2)根据式(8)可以得到输出为y的电路图，如图13所示。

图13 y的电路设计图

图13中输入信号x和z分别经过反相器得到输出信号-x和-z，两个输出信号在和信号y一起经过反相加法运算电路得到输出信号(x-y+z)，该信号经过反相积分器可以得到-y，再经过反相器即可得到输出信号y。

(3)根据式(8)得到输出为z的电路图，如图14所示。

图14中输入信号y经过反相比例运算电路得到的输出信号为-15y，该信号经过反相积分器可以得到-z，再经过反相器即可得到z。

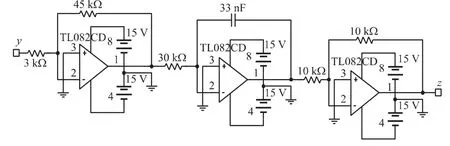
图14 z的电路设计图

2.2 蔡氏电路的Multisim仿真

Multisim软件是加拿大IT公司推出的用于电路仿真与设计的EDA软件，称为“虚拟电子工作台”。该软件具有强大的仿真测试和分析功能，仿真设计精确、可靠［6］。

蔡氏电路的状态方程，本文采用的是通用模块化的设计思想，由反相加法电路、反相积分电路、反相器电路构成通用混沌电路模块，非线性函数部分f(x)=［|x+1|-|x-1|］根据系统方程，加到电路中去［7-8］。即由上一节已经设计好的x，y，z方向电路和f(x)电路组成整体蔡氏混沌电路，具体如图15所示。

图15 Chua状态方程的电路图

通过Mutisim硬件电路仿真得到蔡氏混沌电路的时域波形图及其相图，其结果与MATLAB的数值仿真结果相同，说明了通用模块化混沌电路设计思想及在Multisim软件中的混沌电路仿真应用是完全可行的。波形见图16～图19所示。

图16 x方向时域波形图

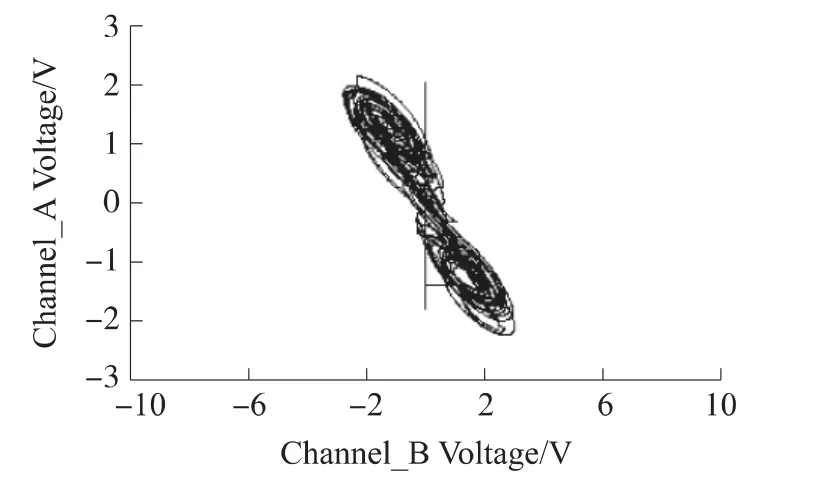
图19 x-z方向相图

3 结论

本文主要介绍了蔡氏混沌电路的通用模块化设计方法在Multisim软件中的仿真实现。虽然该设计方法与只含有4个基本元件和一个非线性电阻组成的典型蔡氏电路相比而言，要复杂一些，但是通用模块化电路的好处是直观明了，具有一定的通用性、所有电路参数均可独立调整，对于了解混沌信号产生过程、制作各类混沌电路均有一定的帮助。该方案顺利通过Multisim软件的电路仿真，与MATLAB数值仿真的结果是一致的。

［1］黄润生，黄浩.混沌及其应用［M］.武汉:武汉大学出版社，2005:12.

［2］蒋国平，陈艳云.蔡氏混沌非线性电路及其频率特性的研究［J］.电气电子教学学报，2002(10):5-7.

［3］禹思敏.混沌系统与混沌电路——原理、设计及其在通信中的应用［M］.2011:4.

［4］禹思敏.用三角波序列产生三维多涡卷混沌吸引子的实验［J］.物理学报，2005(4):1500-1509.

［5］徐伟.基于存储器的三阶JERK混沌电路实验研究［J］.安徽理工大学学报(自然科学版)，2010(4):35-39.

［6］王冠华.Multisim11电路设计及应用［M］.北京:国防工业出版社，2010:1.

［7］刘英明，马艳萍，王东方.混沌电路的仿真研究［J］.佳木斯大学学报(自然科学版)，2006(6):427-428.

［8］王姮，张华.蔡氏电路的SPICE仿真研究［J］.西南工学院学报，1999，14(3):41-46.

蔡氏混沌电路在Multisim软件中的设计与仿真*

徐 伟*，马进颖

Design and Simulation of Chua Chaotic Circuit by M ultisim Software*

XUWei*，MA Jinying
(College of Physical and electronic technology，Yancheng Teachers University，Yancheng Jiangsu224001，China)

The classic Chua chaos circuit is very simple circuit which is capable of generating the chaotic signals. However its parameters of the circuit is essentially fixed，and do not have versatility between different chaotic circuits.It provides the reconstruction of Chua’s chaotic circuit by method ofmodular design based on Multisim software.All parameters of Chua chaos circuit can be adjusted independently.And it is emphasis on how to use diodes and an operational amplifiers to achieve the absolute value circuit of complex nonlinear function，the simulation results of the Chua circuit double scroll attractors is given correspondingly.

Chua chaos circuit;modular design;Multisim simulation;saddle focus;absolute value circuit

10.3969/j.issn.1005－9490.2013.06.034

TN711 文献标识码:A 文章编号:1005－9490(2013)06－0904－06

项目来源:江苏省高等学校2013年度大学生实践创新训练计划项目(201310324058X)

2013-04-11修改日期:2013-05-10

EEACC:1250

徐 伟(1982-)，男，汉族，江苏省盐城市人。盐城师范学院物理科学与电子技术学院教师，研究生学历。研究方向为混沌信号的产生与保密通信、智能控制领域方面的研究，xuwei7506@126.com。