四旋翼飞行器建模与PID控制器设计
江 杰 , 岂伟楠
(内蒙古科技大学 信 息工程学院, 内蒙古 包 头 0 14010)
近年来,随着新型材料、微机电(MEMS)、微惯导(MIMU)以及飞行控制等技术的迅速发展,小型四旋翼飞行器得到了进一步的发展,逐渐成为各国科技人员关注的焦点。小型四旋翼飞行器是一种具有4个螺旋桨,并且螺旋桨呈十字交叉结构的旋翼式飞行器,它通过调整4个电机的转速来实现俯仰、横滚、偏航等飞行动作,并具有可悬停、机动性好、结构简单等优点。
飞行控制一直是小型四旋翼飞行器的关键技术,国防科技大学的聂博文设计了基于反步法的控制器,哈尔滨工业大学的王树刚设计了基于H∞回路成形的控制器,东北大学的王丽新设计了基于滑动模态的滑模变结构控制器[1-3]。目前有关于四旋翼飞行器控制算法的研究多集中在非线性控制方面,由于非线性控制对系统模型准确性有很高的要求,在模型误差存在的条件下,PID控制更加有效。本文在四旋翼飞行器动力学建模的基础上设计了PID控制器。
1 四旋翼飞行器动力学模型的建立
恰当的坐标系选取有利于对四旋翼飞行器的运动过程进行分析,在描述四旋翼飞行器绕三坐标轴平动、转动的过程中,常选择载体坐标系。分析、定位飞行器在空间的位置时,则在导航坐标系中研究、分析较为方便。上述定义的两个坐标系如图1所示。
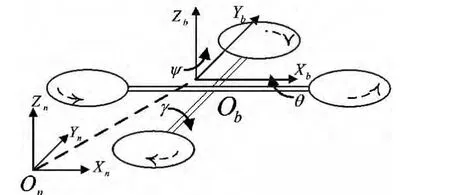
图1 导航坐标系和载体坐标系Fig.1 Navigate and body coordinate system
选取导航坐标系为绝对坐标系,记为n。以原点On为水平面内一点,Xn轴位于水平面内,指向正东方向,其Yn轴位于水平面内并且与Xn轴垂直且指向正北方向,Zn轴与Xn轴和Yn轴构成的平面垂直且方向为垂直向上,符合右手法则。
机体坐标系建立在飞行器机体上,记为b。其原点Ob在飞行器重心位置上,Ob-XbYbZb在小型四旋翼飞行器对称平面内,Xb轴与Xn轴平行且指向右方,Yb轴与Yn轴平行且指向前方,Zb轴与Zn轴平行且指向上方。
机体坐标系绕3个轴旋转与导航坐标系所成的夹角分别称为俯仰角θ、横滚角φ,航向角ψ。姿态角定义如下:
俯仰角θ:为机体坐标系Xb轴和导航坐标系XnOnYn平面的夹角。
横滚角φ:为机体坐标系Yb轴和导航坐标系XnOnYn平面的夹角。
航向角ψ:为机体坐标系Xb轴在导航坐标系XnOnYn中投影与OnXn的夹角。
为在建立飞行器运动方程时考虑所有这些因素将是极其复杂的,因此我们采取抓主要矛盾、略去次要因素的方法进行研究。作如下假设:
1)飞行器为刚体且质量是常数;
2)地面坐标系为惯性坐标系;
3)忽略地球曲率,即采用所谓的平板地球假设;
4)重力加速度不随飞行高度而变化;
5)对于面对称、轴对称布局的飞行器,其不仅几何外形对称,而且内部质量分布也对称[4]。
在机体坐标系中,定义推力T(T∈R)为飞行器4个旋翼产生升力总和,因此在机体坐标系中飞行器受到的拉力可以表示为如式(1)所示:
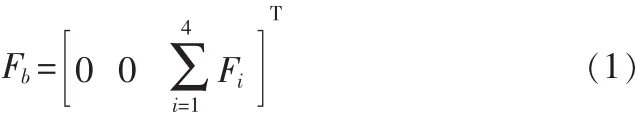
式(1)中 Fi表示四旋翼飞行器第 i(i=1,2,3,4)个旋翼产生的升力,四旋翼飞行器在被看作为刚体的时候,其运动规律可用沿空间三个线坐标和三个角坐标的运动形式来表示,即飞行器的线运动(飞行速度的增减运动、升降运动和侧移运动),以及围绕飞行器机体中心轴转动的角运动(俯仰方向角运动、横滚方向角运动、偏航方向角运动)。
首先讨论小型四旋翼飞行器在导航坐标系下沿Xb、Xb、Zb3个轴向的线位移运动方程,如式(2)所示:
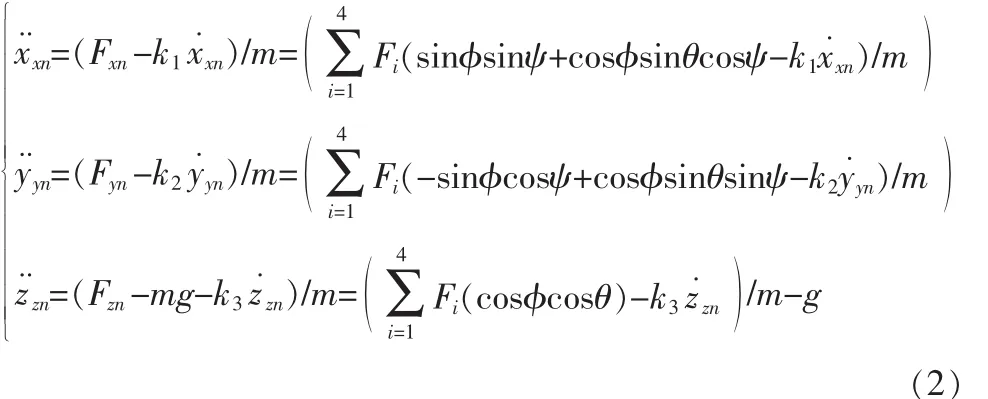
其中系数ki(i=1,2,3)表示飞行器在导航坐标系中Xn、Yn、Zn方向上的空气阻力系数,由于飞行器在实验阶段处于低速飞行状态,故该系数可以忽略不计。
飞行器绕质心的旋转的角运动包括俯仰角运动、横滚角运动、偏航角运动,根据力矩平衡原理,得到飞行器在导航坐标系下 Xn、Yn、Zn的角位移方程,见式(3)所示:

式中l为飞行器重心到每个螺旋桨的距离;Mi为第i个螺旋桨产生的转动力矩;I为对应轴的转动惯量,=Iz/l,Ki(i=4,5,6)表示飞行器在角位移运动时的空气阻力系数,其中k=k6l,选取式(4)作为四旋翼飞行器控制系统控制输入量:

式(4)中 u1、u2、u3、u4分别为飞行器的升力、横滚力、俯仰力、偏航力。把四旋翼飞行器垂直、俯仰、横滚、偏航通道的4个输入力用矩阵的形式表示为U=[u1u2u3u4]T。把四旋翼控制系统模型分解为飞行器在上述4个独立的运动控制通道,把式(4)带入到式(2)、(3)中,在忽略与速度平方成比例的空气阻力系数ki的条件下[5-6],系统数学模型可以简化为如式(5)所示:

2 PID控制器设计

采用准LPV法对四旋翼飞行器控制[8]系统建立线性空间模型,使用了近似方法并忽略了四旋翼飞行器力和力矩之间弱耦合[7]。建立四旋翼飞行器系统的一个状态空间实现,其中设定飞行器垂直方向速率z˙、俯仰方向角速率θ˙、横滚方向角速率φ˙和偏航方向角速率ψ˙为4个输出变量;x轴方向线速率,y轴方向线速率,z方向线速率z,俯仰方向角加速率θ˙,滚动方向角加速率φ˙,偏航方向角加速率ψ˙,重力加速度 g,俯仰角 θ,横滚角φ和偏航角ψ为状态变量;输入为u1、u2、u3、u4所构成的矩阵,进一步根据准LPV法可以得到四旋翼飞行器系统状态空间如式(6)所示:


通过求解相关系数矩阵,带入飞行器实际模型参数,并在小角度范围下有cosθ=1cosφ=1,得到在状态空间形式下的传递函数,如式(10)所示:
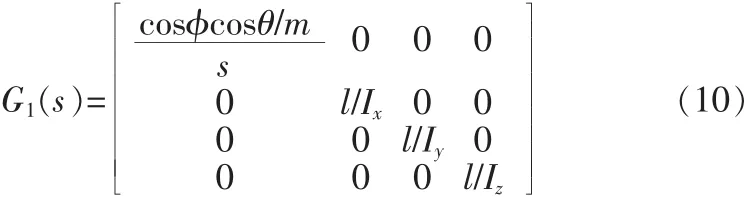
四旋翼飞行器在实验过程中机体处于小角度范围为进行变化进行,故可以有 cosθ=1cosφ=1,式(10)简化为:

系统最终的线性模型由飞行器机体模型和无刷电机模型共同组成,无刷直流电机被描述为一个一阶惯性环节,电机调速器控制信号和旋翼产生升力之间的传递函数为:

d为电机电子调速器控制信号与电机升力之间的比例系数,比例系数的选取一般是通过实验测量得到的d值的大小对系统仿真影响较小,因此在四旋翼飞行器控制器设计中取d=1来进行系统仿真,并设旋翼升力F和Ud之间的关系为G2(s),G2(s)如式(14)所示:
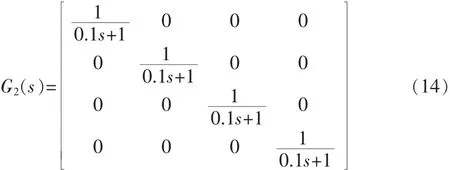
故系统最终的线性模型为:

根据如式(15)所示传递函数对飞行器4个通道设计控制器,其中在垂直速率方向(kP=15、kI=0.01),偏航角速率方向(kP=3,kI=0.01)使用 PI控制算法,在俯仰角速率方向(kP=3.8,kD=1.1)、横滚角速率方向上(kP=3.8,kD=1.1)设计 PD 控制器。当t=3 s时各通道分别加入脉宽为3 s的方波信号,仿真结果如图 2、图3、图4、图5所示。
3 结 论
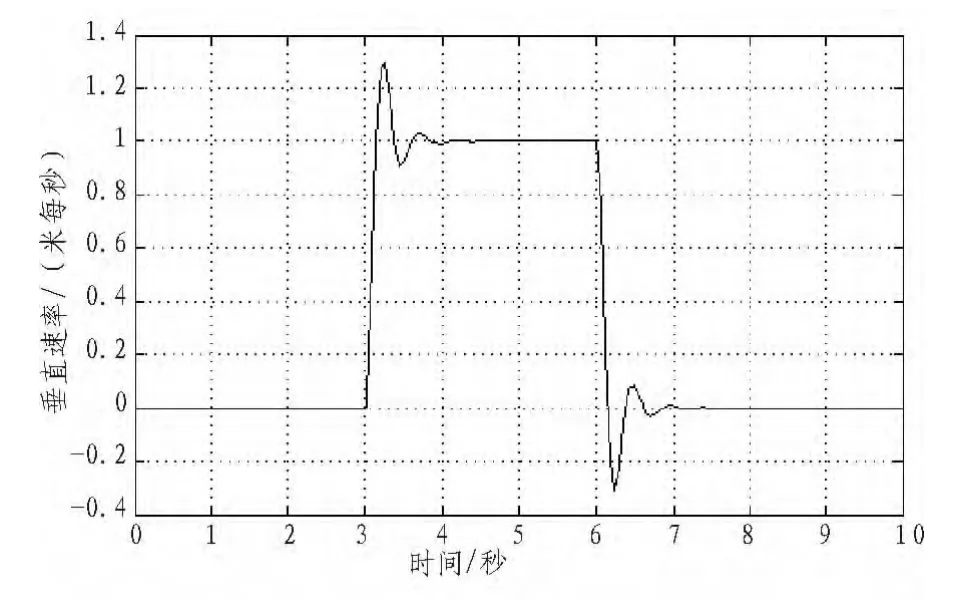
图2 垂直速率通道方波响应Fig.2 Vertical speed of square response

图3 俯仰角速率通道方波响应Fig.3 Pitch speed of square response
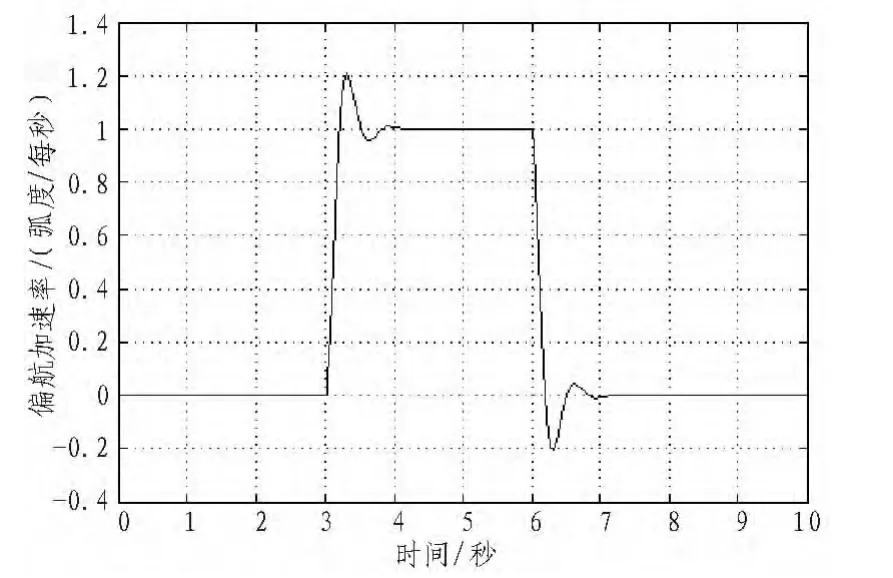
图5 偏航角速率通道方波响应Fig.5 Yaw speed of square response
通过观测系统在方波信号下的响应曲线图2、图3、图4,在系统动态性能指标中,上升时间﹤0.5秒,调节时间﹤1秒,超调量﹤20%,设计的控制器在垂直速率、俯仰速率、横滚速率、偏航速率通道上满足系统控制要求。
[1]王树刚.四旋翼直升机控制问题研究[D].哈尔滨:哈尔滨工业大学,2006.
[2]聂博文.微小型四旋翼无人直升机建模及控制方法研究[D].长沙:国防科学技术大学,2006.
[3]王丽新.基于滑模理论的四旋翼直升机的姿态控制研究[D].沈阳:东北大学,2009.
[4]吴森堂,费玉华.飞行控制系统[M].北京:北京航空航天大学出版社,2005:46-47.
[5]Castillo P,Dzul A,Lozano R.Real-time stabilization and tracking of a four-rotor miniRotorcraf[H].IEEE Transactions on Control Systems Technology,2004,12(4):510-516.
[6]Bouabdallah S,Noth A,Siegwart R.PI vs LQG control techniques applied to an indoor micro quadrotor[J].IEEE Trans on Intelligent Robots and Systems,2004(3):2451-2456.
[7]Papageorgiou G,Glover K.Taking robust LPV control into flight on theVACC harrier[C].Proceedings of the 39th IEEE conference.on Decision and Control,2000:4558-4564.
[8]吴中华,贾秋玲.四旋翼几种控制方法研究[J].现代电子技术,2013(15):88-90,94.
WU Zhong-hua,JIA Qiu-ling. Severalcontrolmethods research of quadrotor[J].Modern Electronics Technique,2013(15):88-90,94.

