求解线性等式约束优化问题的移动渐近线法
张书花,李艳龙,李 磊,景孟旗
(1,4、河海大学水利水电学院,南京,210098;2,3、河海大学力学与材料学院,南京,210098)
0 引言

一般的数值方法在求解大规模线性约束优化问题时,达不到计算时间和内存的要求。因此本文对大规模优化问题,首先运用信赖域方法将原优化问题的设计变量转换为搜索方向,再结合零空间方法和线搜索技术对移动渐近函数进行构造,运用算例验证了该算法在求解大规模线性等式约束优化问题方面的有效性。通过求解问题得到下降搜索方向,然后计算步长,得到下一迭代点
Svanberg在1987年对优化问题首次提出MMA法,用移动渐近线函数逼近优化问题中的目标和约束函数,从而产生子问题。通过求解子问题,最终求得约束优化问题的最优解。本文在文献[6,7]的基础上,对移动渐近线函数进行了深入的研究,构造了含参数的新的移动渐进线函数,并形成新的问题。子问题是严格凸且可分的,不需更新信赖域半径。在此基础上,获得了一个解线性等式约束优化问题的新MMA算法。讨论了参数的选取准则,证明了新算法的全局收敛性,并通过试验结果得出算法的有效性。
1 新MA子问题
文献[6]对MA法提出,并用于线性等式约束优化问题(1)。在当前迭代点处构造的子问题:
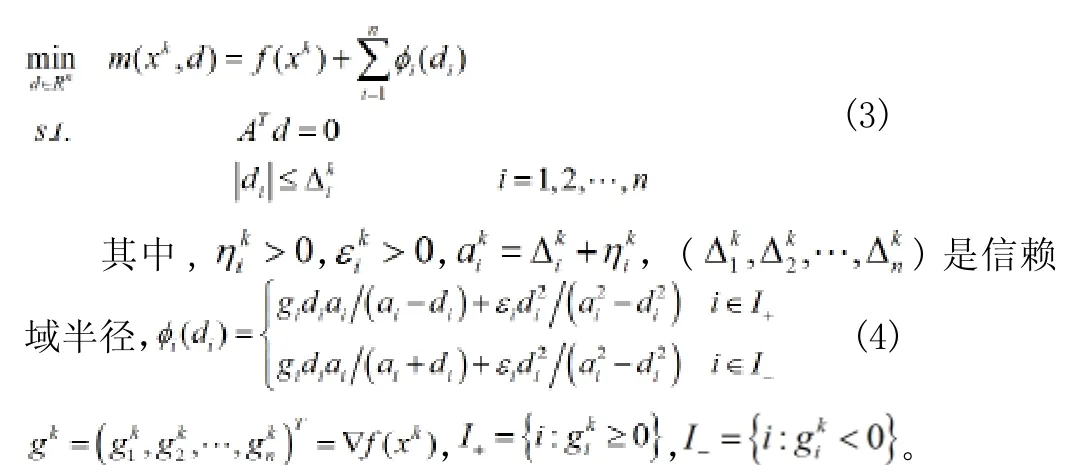
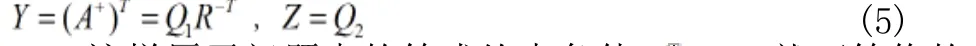


2 新MMA算法步骤及收敛性

类似于文献[6]中定理的证明,得到算法1具有全局收敛性。
3 数值验算
在本节中,进行数值试验:将算法1与文献[3]中的MMA算法(以下简称为OMMA算法)、投影梯度算法(以下简称为PGM算法)进行比较。

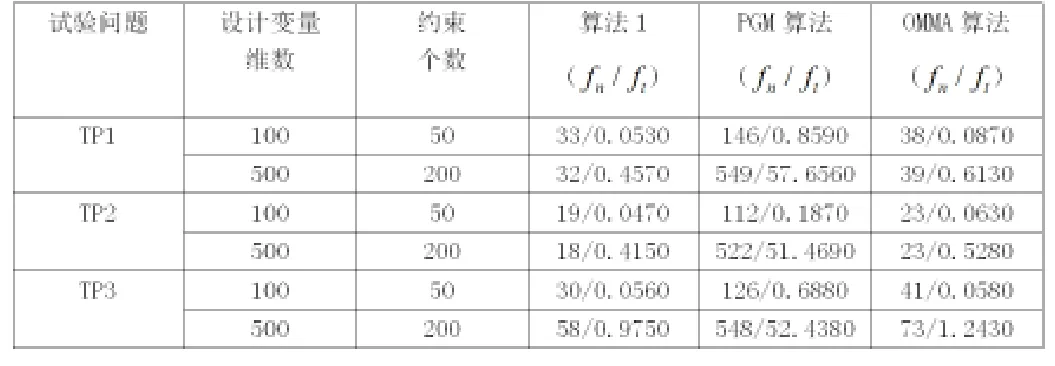
表1 : 算法1与PGM算法、OMMA算法的运行结果Table 1: The numerical results of algorithm 1、PGM and OMMA
由计算结果表1可以看出,对于优化问题,算法1的效果优于OMMA算法和PGM算法,算法1的运行时间也少于OMMA算法和PGM算法,因此,算法1在解大规模线性约束优化问题方面非常可取。
4 结论
为了有效地求解线性等式约束优化问题,本文构造了一个新的移动渐近线函数,进而建立了新的移动渐近线子问题,并讨论了子问题中参数的选取策略,求出子问题的最优解,然后将此最优解作为原问题的一个下降方向进行线搜索。我们对该算法进行数值试验,得出算法1是一种有效算法,适合求解大规模线性等式约束优化问题,有可能求得全局最优解,新的MMA算法可应用于大型工程计算。
[1] Bulteau J P,Vial J P.A restricted trust-region algorithm for unconstrained optimization, J Optim.Theory Appl., 1985, 47:413-435
[2] Shi Z J, Guo J H. A new trust region method for unconstrained optimization. Journal of Computational and Applied Mathematics, 2008, 213:509-520
[3] Fletcher R. Practical methods of optimization.Chichester: John Wiley and Sons,1981.
[4] 袁亚湘,孙文瑜. 最优化理论与方法[M]. 北京:科学出版社,1997
[5] Svanberg K.The method of moving asymptotes—a new method for structural optimization[J].International Journal for Numerical Methods in Engineering, 1987, 24(2): 359-373
[6] 王海军. 解非线性最优化问题的移动渐近线法及应用;[D]南京,南京航空航天大学;2010
[7] 胡平,贾朝辉,倪勤.一种解无约束优化问题的新移动渐近线算法;工程数学学报;2012

