基于系统性金融风险度量方法的宏观审慎监管研究

常 嵘

(南开大学经济学院金融系，天津300071)

一、问题的提出

在2008年国际金融危机发生后，各国在理论、实践和政策制定方面对如何防范系统性金融风险都进行了新的探索，其中最重要的变化是对宏观审慎监管的强调，相关的研究也有很多。根据Borio(2003)，系统性金融风险有两个来源，一是时间维度下金融体系的顺经济周期性，这体现为各金融机构对宏观经济风险的共同暴露;二是横截面或空间维度下金融体系的风险传染性，即由个别金融机构倒闭引起的金融危机。与此相对应，宏观审慎监管也包含两个方面的内容——时间维度下的逆周期政策和空间维度下系统重要性金融机构的识别以及监管。

宏观审慎监管的出发点是降低系统性金融风险发生的可能性，所以相应的政策制定应当以准确衡量系统性金融风险为基础。在危机之前，有关系统性金融风险度量方法的研究以基于银行资产负债表和宏观经济变量的综合指标法和预警模型为主，在危机之后则多以市场数据为基础，将金融工程领域的思想引入模型的开发，并注重考虑微观金融机构之间的内在关联(朱元倩和苗雨峰，2012)。虽然系统性金融风险的度量方法在数据使用、模型开发以及度量视角方面都更加成熟，但直到目前，这些方法并未在宏观审慎监管的具体实践中找到用武之地，宏观审慎监管的政策制定过程仍然缺乏对系统性金融风险的客观评估，随意性和主观性较强。实践中的监管措施强调可操作性，但又不能因此失去有效性，就如何运用科学的系统性金融风险度量方法来指导宏观审慎监管政策的制定而言，还没有可供参考的模式，本文将以逆周期资本缓冲机制的建立与系统重要性金融机构的识别为例，结合中国的现实情况对此作一个初步的探索，以期对提高宏观审慎监管政策的科学性有所启示。

二、逆周期资本缓冲机制的建立与宏观压力测试

(一)逆周期资本缓冲机制的逻辑与建立原则

金融体系自身的顺周期性在经济上行期会导致资产价格泡沫的累积，在经济下行期又会加剧风险的传播，这实际上是市场失灵的一种表现。单家金融机构为了追求自身利益的最大化，在经济繁荣、流动性宽松时会扩张信贷、购买资产，在经济衰退、流动性紧缺时会减少信贷、出售资产，但是如果每一家金融机构都作出同样的选择，就会使这种从微观层面看来是审慎合理的行为演变成整个金融体系的内生性风险。为了弥补这一市场失灵，政府应该从宏观金融稳定的角度出发，建立起更具前瞻性的逆周期监管制度安排，目的在于促使各金融机构能够以更长远的眼光准确评估自身风险，激励金融机构达到更高的审慎标准。逆周期资本缓冲即是其中最重要的一项制度安排。

逆周期资本缓冲机制的目的是保证银行的资本计提能够考虑宏观金融状况，当系统性风险在经济上行期逐步累积时，银行除了根据微观审慎层面的内部评级法计算所需资本外，还应针对系统性风险，从宏观审慎角度增加一部分逆周期缓冲资本，计提的逆周期资本应采用核心一级资本或其他吸收损失能力强的资本形式。与此相反，当经济下滑时，银行的资产风险明显加大，此时降低资本充足率的要求可以使银行释放资本缓冲，吸收损失和上升的资产风险，防止信贷过度紧缩。建立逆周期资本缓冲机制需要明确两个基本要素:一是银行积累和释放逆周期资本缓冲的时点;二是逆周期资本缓冲的计算方法。

就时点而言，关键是为判断系统性风险的大小寻找能够前瞻性地识别金融周期的指标，该指标可称为景气指数或金融稳定系数，它的上临界点将触发逆周期资本缓冲的计提，意味着信贷增长不可持续以及金融系统性风险正在逐步累积;下临界点将触发逆周期资本缓冲的释放，以缓解信贷供给的减少。巴塞尔银行监管委员会2010年颁布的《各国监管当局实施逆周期资本缓冲的指导意见》中给出的参照指标为Credit/GDP缺口(信贷总量与名义GDP的比重对长期趋势的偏离)，并指出当Credit/GDP缺口≥2%时开始计提逆周期资本缓冲;当Credit/GDP缺口≥10%时，逆周期资本缓冲达到最大值VBmax且维持不变;如果缺口值处于2% －10%之间，则逆周期资本缓冲在(0，VBmax)的范围内递增。但由于没有提及释放逆周期资本缓冲的Credit/GDP缺口下临界点，该指导意见其实并不完整。此外，在制定宏观经济稳定政策时，缺口类指标的可靠性往往被经济学家所质疑(Staiger等，1997;Orphanides和 Van Norden，2002)，即样本末期t的趋势估计值是不可靠的，随着时间的推移，样本序列变长后再次确定变量的长期趋势时，t期的趋势值将发生较大的变化，而政策制定者所需的当前趋势值的估计正是样本末期的值。Edge和Meisenzahl(2011)的研究证实了Credit/GDP缺口也是如此。Repullo和Saurina(2011)指出了Credit/GDP缺口指标的另一个不足之处，即Credit/GDP缺口与GDP的增长率负相关，这会导致逆周期资本缓冲在经济上行期可能无法有效计提，而在经济下行期又不能及时释放。因此，以Credit/GDP缺口来判断计提逆周期资本缓冲的时点存在一定的问题。

就目前的研究来看，逆周期资本缓冲的计算方法有两种基本思路(Gordy和Howells，2006)。一是改变风险加权资产的计算方法，即要求银行跨期平滑内部评级法下的风险权重，从时点评级法(point－in－time，PIT)转为跨期评级法(through－the－cycle，TTC)，以评估借款人在一个经济周期内发生违约的可能性。二是改变资本充足率的标准，即在最初的由时点评级法确定的资本要求之上，乘以逆周期乘数，经济繁荣时，逆周期乘数大于1，经济衰退时，逆周期乘数小于1。前者所要求的跨期评级法涉及的技术难度较大，银行很难将纯粹由经济周期导致的违约风险和由非周期性因素导致的违约风险变化区分开来(Financial Service Authority，2009)，这种困难意味着银行在采用跨期评级法提取逆周期资本缓冲时的随意性较大，不易监督。因此，直接通过逆周期乘数改变资本充足率标准的做法有更强的可操作性。逆周期乘数由前述的判断时点的周期指标导出，但有关逆周期乘数推导方法的研究还很少，Repullo等(2010)给出的一种形式为:

其中，gt是某个周期指标的变化率，g是该指标的长期均值，σg是长期标准差，N为标准正态分布的累积分布函数，α为正参数。首先提取按照时点计算法得到的银行业整体资本充足率的长期趋势，然后确定α使调整后的资本充足率与趋势的均方根偏差(rootmeansquaredeviation)最小。

可以看出，上述做法是根据经济状况的冷热来调整银行资本充足率的要求，以确保银行在整个经济周期内的资本充足率维持在接近长期趋势的稳定水平，但这种方法至少存在两个问题。第一，从逆周期乘数μt的表达式可知，μt的选择依赖于周期指标gt的缺口值，而正如上文所述，缺口值的可靠性值得怀疑。第二，该做法根据过去一段时间内的数据计算出α，从而把经济景气指标与逆周期乘数联系起来，因此本质上是面向历史的，随着时间的推移，α的值也将发生变化，这意味着通过以历史数据决定的α来确定未来的逆周期资本充足率并不恰当。另外，这种“一刀切”式的做法不够合理。首先，计提资本是有成本的，根据单家银行在经济下行期抵抗风险的能力不同，逆周期乘数应当有所调整，抗风险能力高的银行可以适当减少逆周期资本缓冲。其次，不同银行的外部融资约束存在差异，比如在中国，国有及股份制银行的外部融资约束小，而城市及农村银行则缺乏外部融资渠道。逆周期资本缓冲的原意是在经济繁荣时，通过提高资本充足率的标准督促银行用更多的留存利润建立资本缓冲，从而抑制银行过度放贷，但如果银行有较多的外部融资渠道，逆周期资本监管的作用就会相对有限。因此在制定逆周期超额资本要求时，应计算不同银行外部融资约束的大小①一种可行做法是估计银行贷款对留存利润的敏感度。，约束小的银行应适用更高的标准，这样才能发挥逆周期资本缓冲机制的作用。

(二)宏观压力测试在逆周期资本缓冲机制中的应用

在构建逆周期资本缓冲框架时，虽然Credit/GDP缺口是目前监管当局推崇的指标，但根据前文的分析，无论是确定缓冲资本的计提时机，还是计算缓冲资本的计提比例，以Credit/GDP缺口为基础的方法都不能较准确地根据历史数据做出前瞻性判断，也就难以实现设立逆周期资本缓冲机制的初衷。而且Credit/GDP缺口并不能全面衡量宏观经济周期内系统性风险的变化，尤其是缺乏对经济下行期缓冲资本释放时点的判断。

结合以上对逆周期资本缓冲机制设置意图和实践要求的分析，我们认为在各种系统性金融风险的度量方法中，宏观压力测试是一个比较合适的切入点。宏观压力测试通常用来衡量未来可能发生的不利的宏观经济冲击对系统性金融风险的影响，但我们可以根据其原理，将该方法用于评测当未来经济转好时金融体系的风险变化情况。不难看出，宏观压力测试衡量系统性风险的出发点是逆周期的，具有前瞻性的，这与逆周期资本缓冲的内在逻辑相一致。另外，压力测试最早是用在微观领域的，在宏观压力测试的基础上，以单家银行为对象的微观压力测试结果可以作为缓冲资本差异性要求的依据。

宏观压力测试的第一步是尽可能准确地估计作为风险驱动因素的经济变量与银行资产质量之间的动态关系，为此应当考虑包含风险指标与宏观经济变量的VAR模型(Hoggarth等，2005)，而不是通过单一方程估计宏观经济冲击对银行风险的影响。在风险指标的选取方面，由于此处宏观压力测试的目的是确定逆周期资本缓冲比率，因此模型关注的重点为宏观经济冲击对银行业资本充足率的影响①在中国人民银行公布的《中国金融稳定报告2012》中，银行业的压力测试内容是检测不同程度的负面冲击对银行体系资本充足率的影响。。宏观压力测试模型的具体设定如下:

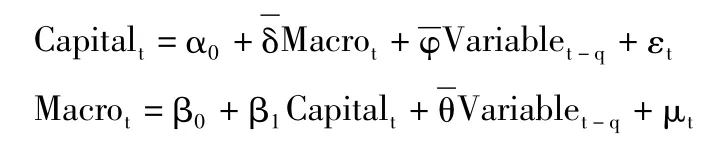
Capitalt代表银行业的整体资本充足率;Macrot是表征宏观经济状况的指标，为n×1向量，这些指标的选取需要充分考虑中国银行业经营的现实情况，比如在房地产贷款总量居高不下、经济结构面临深度调整的情况下，应当加入房地产价格指数、国际收支等指标。是所有内生变量的滞后值，为(n+1)×q的矩阵，εt、μt分别是资本充足率和宏观经济状况的随机扰动项，且互不相关。该结构VAR模型考虑了宏观经济冲击对银行资本充足率的持续影响，以及金融体系运行对实体经济的反馈效应。

从宏观压力测试模型到建立逆周期资本缓冲机制的基本思路是:当银行信贷投放出现上升势头时(即经济景气周期上升阶段)，以当前宏观经济变量的取值为基础引入负向冲击，根据上述结构VAR模型的估计结果，采用蒙特卡罗模拟方法得到Macrot受到负向冲击后银行业资本充足率Capitalt的分布，并得到95%的置信水平下资本充足率的极端值RN，如果RN小于一级核心资本充足率的最低要求a，则启动逆周期资本缓冲的计提。然后将上述模拟过程应用到以单家银行为目标的压力测试中，得到各银行在宏观经济负向冲击时资本充足率的极端值RIN和不同银行RIN的分布图。以(a－RN)为基准，分位数α处于50%以下的银行应计提的逆周期资本缓冲率为(a－RN)×(1+α);分位数α处于50%以上的银行应计提的逆周期资本缓冲率为(a－RN)×(1－α)。

同理，当银行信贷投放出现下降势头时(即经济景气周期下降阶段)，引入宏观经济变量的正向冲击，并得到95%的置信水平下资本充足率的取值RP，如果RP大于一级核心资本充足率的最低要求a，则允许释放逆周期资本缓冲。然后以单家银行为目标进行上述模拟过程，得到各银行在宏观经济正向冲击时的资本充足率取值RIP和不同银行RIP的分布图。以(RP－a)为基准，分位数α处于50%以下的银行可以释放的逆周期资本缓冲率为(RP－a)×(1－α);分位数α处于50%以上的银行可以释放的逆周期资本缓冲率为(RP－a)×(1+α)。也就是说，当经济在未来出现好转时，资本充足率改善较大的银行可以释放更多的资本。

在上述逆周期资本缓冲机制下，缓冲资本计提与释放的时点以宏观压力测试对系统性风险的度量结果为判断依据，由于引入了逆向冲击，该结果可以较好地衡量经济繁荣期隐藏的风险累积，以及经济衰退期所暗示的风险化解。在资本缓冲计提与释放比例的计算方面，逆向冲击对银行业整体资本充足率的影响是基准，相应的微观压力测试结果对此基准的修正则体现了不同银行在抵御经济周期逆转风险能力方面的差异，这样可以在减缓银行顺周期行为风险的同时，最大化银行的盈利。

三、识别系统重要性金融机构的两步法框架

(一)金融机构系统重要性的评估方法概述

应G20成员国的要求，国际货币基金组织、国际清算银行和金融稳定理事会于2009年联合发布了《系统重要性金融机构、市场和工具的评估指引》，这一文件对系统重要性金融机构的含义、定性的评估标准和定量的技术方法作了初步说明。如果一家金融机构的倒闭或功能紊乱会给整个金融系统甚至是实体经济带来严重的负面冲击，则该机构具有系统重要性。评估标准包含与金融机构的规模和可替代性有关的直接影响渠道，以及与关联性有关的间接影响渠道;另外，诸如杠杆率、期限错配程度和复杂性等也需要关注，即高风险金融机构的监管标准应当像系统重要性金融机构看齐。评估方法分为指标法和模型法两类。指标法根据评估标准选取具体指标并赋予相应的权重，然后加总出综合值。模型法是从定义出发直接测算金融机构的系统重要性，主要包括网络分析、基于市场数据的组合风险模型、压力测试或情景分析三种方式①压力测试或情景分析检验的是假设的市场冲击对金融机构的影响，与系统重要性的含义并不一致，因此严格来讲不能算作一种评估方法。。

指标法简洁明了，易于计算，但前提是规定好纳入评估的指标和对应的权重，使得到的综合值能够反映出系统重要性的多个维度。巴塞尔委员会2011年公布的《全球系统重要性银行:评估方法及额外损失吸收要求》用指标法评估了全球73家银行的系统重要性，首先是确定五类标准:全球活跃程度、规模、关联性、可替代性和复杂性，权重各占20%，然后在每一类标准中选取相对应的指标共计12个，每个具体指标的权重在子类中平均分配，但指标的选择以及按照平均思想确定权重的方法仍然缺乏严谨性和逻辑基础。与此形成对比的是，模型法的逻辑科学严谨，有关金融机构系统重要性的研究文献也大多围绕模型法展开。我们在此将对网络模型和组合风险模型的核心思想做出归纳总结，并进一步指出可能的拓展方向。

网络分析的核心是根据金融机构资产负债表之间的相互关联，构建风险敞口矩阵，在此基础上，模拟某家金融机构的倒闭引发的一系列损失和倒闭的过程(Wells，2004)。具体来讲，矩阵的元素代表j对i的负债，假设j最先倒闭，则i遭受的损失为，θ是损失率，ci是i的资本金，当＞ci时，i也会倒闭，继而给k带来θxki的损失，于是k遭受的损失累计为θ(+)，当θ+)＞ck时，k也会倒闭，这样一轮一轮地持续下去，直到不再有金融机构倒闭为止，则j的系统重要性由其引发的总损失L或倒闭的金融机构总数目N来衡量。

该模拟过程真实展现了一家金融机构的倒闭给整个金融系统带来的风险，这与系统重要性的定义相符，但在实际应用中存在的两方面问题会导致一定程度的偏差。一是θ只能依靠假设来确定，不同轮次、不同金融机构之间的θ也被设定为相同值;二是研究人员往往只能获得一家金融机构对其他金融机构的负债总额，因此双边风险敞口矩阵的数据需要通过额外的假设(如熵最大化)来估计，有失真实②虽然这是大多数研究所使用的假设，但也有例外，比如黄聪和贾彦东(2010)直接利用中国人民银行支付系统的银行间支付数据实证分析了中国的银行网络结构。。另外还需指出的是，目前有关网络分析的研究多局限于银行间市场，忽略了对证券、保险、信托公司等其他金融机构的系统重要性分析;而且即使是评估银行的系统重要性，也不能仅关注银行部门之间的关联，因为通过表外业务等方式，银行与其他金融机构之间也会有大量的资金往来，比如中国现阶段存在的银信、银证、银基、银保合作模式，其中隐藏的风险不容忽视。

如果把整个金融体系看做一个资产组合，就可以用组合风险模型的原理来测度各金融机构的系统重要性，这主要分为两条路径:自下而上(bottom－upmeasure)和自上而下(top－down measure)。自下而上法立足于单家金融机构陷入紊乱后对整个金融体系的影响，最具代表性的是Adrian和Brunnermeier(2011)提出的△CoVaR。金融机构i的CoVaR是以i的状态为条件的金融体系的VaR值，i在危机和正常两种状态下对应的CoVaR的差值为△CoVaR，它代表了i的系统重要性。实证研究中先是用分位数回归来估计危机情形下i的股票收益率与金融系统的综合收益率之间的关系，分位数水平q一般选择1%或5%;然后根据收益率的历史数据得到i在q和50%置信水平下的VaR值(分别代表i处于危机和正常两种状态)，带入估计方程得到相应的CoVaR和i的△CoVaR，即③M为决定股票收益率动态特征的状态变量。:

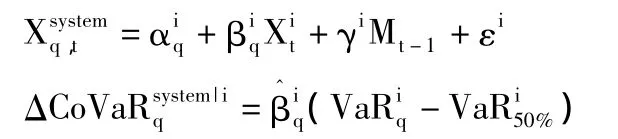
由于是从VaR发展而来，△CoVaR的不足之处在于它没有考虑置信水平之外的风险，而真实危机的发生却往往与黑天鹅事件有关，体现的恰恰是尾部风险。Acerbi等(2008)提出的期望损失(Expected Shortfall，ES)概念描述了尾部风险的期望值，弥补了VaR的缺陷。我们可以借鉴△CoVaR的思路，尝试构建△CoES指标来衡量金融机构的系统重要性，具体做法是根据i与金融体系的历史收益率数据的分布图，得到两者在不同分位数水平下的ES，并进行q(1%或5%)水平下的分位数回归，然后将i在q和50%分位点下的ES带入回归方程得到两种状态对应的CoES，相减得△CoES。

自上而下法的基本思路是将系统性风险分配给各金融机构，按照分配方式的不同，可分为参与法(participationapproach)和贡献法(contributionapproach)。在参与法中，金融机构i的系统重要性为整个金融体系出现危机时i所遭受的损失，即E(Li∣e(N))，其中e(N)代表整个金融系统陷入危机这一事件，Li是 i的损失，E代表损失的期望值。由Acharya等(2010)提出的用系统预期损失(SystemExpected Shortfall，SES)来衡量金融机构的系统重要性就是参与法的典型例子。贡献法将合作博弈中分配整体支付的方式运用到金融系统中，将特征函数ϑ定义为子系统Nsub到风险的映射，从而以沙普利值(Shapley Value)来衡量每个金融机构的系统重要性(Tarashev等，2010):

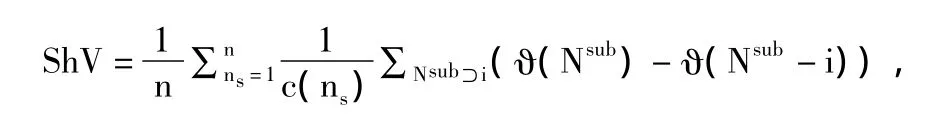
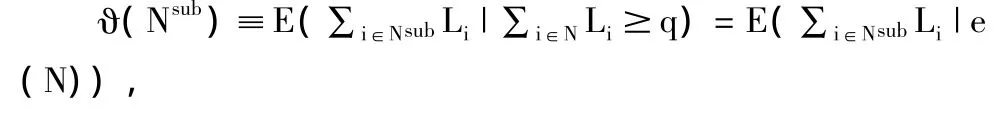
那么金融机构i的沙普利值等于E(Li∣e(N))，由此可见，参与法实际上是贡献法的一种，也就是说，沙普利值框架可以概括衡量系统重要性的自上而下法，特征函数ϑ代表了系统性风险的不同分配方式。根据参与法所对应的ϑ，i对任一金融子系统的边际风险贡献都为E(Li∣e(N))，这显然忽略了不同子系统内金融机构之间关联结构的差异性，但金融机构的关联对于系统性风险的分配是十分重要的，因为除了自身对外生冲击的风险暴露，与其它金融机构之间的双向风险传染也会影响一个金融机构对系统性风险的贡献。为了克服参与法所对应的ϑ的不足，Drehmann和Tarashev(2011a)给出了ϑ的如下形式:

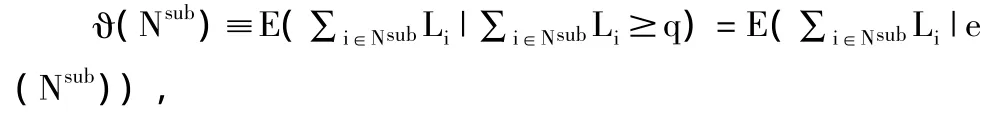
根据该ϑ所计算的沙普利值充分考虑了i对风险传递与扩散的影响，从而更准确地衡量了金融机构的系统重要性。计算ϑ(Nsub)的关键是估计子系统Nsub中各金融机构的联合损失分布函数，从而计算出尾部事件发生时的期望损失，对这一分布函数的估计不仅要考虑外生冲击下的违约概率，还应考虑金融机构之间的违约传染概率，在这种情况下，如何快速精确地计算金融机构组合的损失概率分布是目前系统性金融风险研究的难点。

(二)指标法与模型法相结合的评估框架

根据以上分析可以看出，模型法虽然逻辑严谨，方法科学，但对数据的要求高，计算复杂，公众难以理解，单个金融机构也很难用模型法来评估自己的系统重要性(Drehmann和Tarashev，2011b)。另外，由于模型参数是根据历史数据估计的，为了保证模型的有效性，需要以较高的频率重新估计模型，而在数据收集难度大以及计算复杂的情况下，做到这一点将耗费大量的成本。因此从监管实践的角度来讲，指标法更具有可操作性，比如巴塞尔委员会2011年采用指标法对全球系统重要性银行进行了评估;中国银监会在2010年颁布的银行业实施新监管标准的指导意见中指出，评估国内的系统重要性银行将主要考虑规模、关联性、复杂性和可替代性等四个方面的因素。然而就目前的监管实践而言，评估金融机构系统重要性的指标体系及相应权重的制定仍然缺乏科学的理论基础，如何以科学严谨的模型法来指导实践中的系统重要性评估是一个容易被忽略但又十分重要的问题。

事实上，指标法与模型法之间存在着因果关系。指标法是面向过程的评估方法，即从多角度出发，根据各金融机构的现实经营状况来推断其潜在的系统重要性;模型法是面向结果的评估方法，模型内部的运算过程是一个黑箱，最终的输出结果直接指向系统重要性的大小，而打开黑箱，揭示输出值背后原因的正是指标法中的多个维度。因此，我们结合指标法和模型法各自的优点，提出下面的两步法作为识别系统重要性金融机构的方法论。

第一步是选择模型，通过其输出值测度各金融机构的系统重要性;第二步，将输出值作为因变量，按照规模、关联性、可替代性和复杂性等标准选取指标作为自变量，通过回归分析得到各指标的估计系数及其显著性。系数显著不为零的指标进入评估体系，而且由于估计系数体现了指标与系统重要性之间的联系，因此其大小可被视为赋予各指标的权重。利用模型法测度系统重要性在进行过一次之后可以停止较长时间，因为它主要是为第二步确定权重服务的，在评估体系确立之后，根据固定的权重与未来不断变化的指标值，监管者就能较容易地对各金融机构的系统重要性做出动态评估。由此可见，两步法评估框架融合了模型法和指标法，较好地兼顾了科学性和简明性，有利于准确并且持续地评估金融机构的系统重要性。

就中国的现实状况而言，由于已上市的金融机构数量还比较少，直接用基于市场数据的组合风险模型来确定金融机构的系统重要性会受到较大限制，但上述的两步法能够突破这一限制。如前所述，用模型法得到的系统重要性测度只是第一步，它的主要作用是在第二步中通过回归分析揭示出系统重要性与指标之间的内在联系，因此可以将样本范围限制在已上市的金融机构之中，通过它们的系统重要性测度与指标值之间的关系构建出指标体系，然后在该指标体系下计算出各个金融机构的指标综合值，并据此对金融机构的系统重要性进行排序。

对监管者来讲，还需要为上述排序划定界限，以确定系统重要性金融机构(Systematically Important Financial Institutions，SIFIs)的名单，而这将不可避免地带有一定的主观色彩。正如周小川(2011)所指出的那样，处于临界点附近的金融机构会有两种心理，如果被划入SIFIs，则表明了自己的重要地位;但另一方面，作为SIFI，将面临更高的资本要求和更严格的监管，这就有可能降低自己的资本回报率。在确定划分标准的讨论中，周小川(2011)曾提到相对系数的方法，即以规模位居第五的交通银行为临界点，对于规模在此之下的银行，将该银行的资产与交通银行资产的比例作为相对系数，当该系数小到一定程度时，可以忽略不计，视同为零。由于以规模这一单独指标来衡量金融机构的系统重要性不够全面，我们可以用指标综合值来代替规模，然后按照上述的相对系数方法划定系统重要性金融机构。

四、结 语

在2008年的金融危机之后，宏观审慎监管受到了监管当局和学者的更多重视。对系统性风险的准确衡量是保证宏观审慎监管有效性的基础，但实践中的监管政策制定与理论界对系统性风险度量的研究存在着明显的分离。本文以逆周期资本缓冲机制与系统重要性金融机构的识别为例，分析了现行宏观审慎政策的不足之处，并就如何运用已有的系统性风险度量方法来更好地指导政策实践做了探索性的思考。

在逆周期资本缓冲机制方面，本文从宏观压力测试的原理出发，探讨了逆周期资本缓冲的计提、释放时点和计算方法。逆周期资本缓冲的逻辑是基于整个经济周期内，从未来经济形势发生逆转的角度来看待系统性风险，这与宏观压力测试的原理相似，而且在宏观压力测试的框架下，还可以分析正面经济冲击对金融体系的影响，从而有助于判断缓冲资本释放的时机。不过需指出的是，对于如何应用宏观压力测试来建立逆周期资本缓冲机制，本文只是给出了初步的设想，相关研究仍有待于进一步的完善。

在评估金融机构的系统重要性方面，本文设计了一个两步法框架，根据模型法对金融机构系统重要性的衡量结果来确定指标及相应的权重，这样就可以将模型法的科学性融入到更具可操作性的指标法中，从而有助于监管者准确地对金融机构的系统重要性进行持续的动态评估。

［1］黄聪，贾彦东:《金融网络视角下的宏观审慎管理——基于银行间支付结算数据的实证分析》，《金融研究》，2010年第4期。

［2］周小川:《金融政策对金融危机的响应——宏观审慎政策框架的形成背景、内在逻辑和主要内容》，《金融研究》，2011年第1期。

［3］朱元倩，苗雨峰:《关于系统性风险度量和预警的模型综述》，《国际金融研究》，2012年第1期。

［4］Acerbi C.，Nordio C.and Sirtori C.Expected shortfall as a tool for financial risk management.Working paper，2001.

［5］Acharya V.，Pedersen L.H.，Philippon T.and Richardson M.Measuring Systemic Risk.New York University working paper，2010.

［6］Adrian T.and Brunnermeier M.K.CoVaR.Princeton University working paper，2011.

［7］Basel Committee on Banking Supervision.Guidance for national authorities operating the countercyclical capital buffer，2010.

［8］Basel Committee on Banking Supervision.Global systemically important banks:Assessment methodology and the additional loss absorbency requirement，2011.

［9］Borio C.Towards a macroprudential framework for financial supervision and regulation.BIS working papers，No.128，2003.

［10］Drehmann M.and Tarashev N.Measuring the systemic importance of interconnected banks.BISworking papers，No.342，2011a.

［11］Drehmann M.and Tarashev N.Systemic importance:some simple indicators.BISquarterly review，2011b.

［12］Edge R.M.and Meisenzahl R.The unreliability of credit－to－GDP ratio gaps in real－time and the implications for countercyclical capital buffers.Mimeo，2011.

［13］Financial Services Authority.A regulatory response to the global banking crisis.Discussion Paper，2009.

［14］Financial Stability Board.Intensity and effectiveness of SIFI supervision:recommendations for enhanced supervision，2010.

［15］Gordy，M.and Howells B.Pro－cyclicality in Basel II:can we treat the disease without killing the patient.Journal of Financial Intermediation，2006(15):395－417.

［16］Hoggarth G.，Sorensen S.and Zicchino L.Stress tests of UK banks using a VARapproach.The Bank of England’s working paper series，No.282，2005.

［17］International Monetary Fund，Bank for International Settlements，and Financial Stability Board.Guidance to Assess the Systemic Importance of Financial Institutions，Markets and Instruments:Initial Considerations，2009.

［18］Orphanides A.and Van Norden S.The unreliability of output－gap estimates in real－time.Review of Economics and Statistics，2002(84):569 －583.

［19］Repullo R.，Saurina J.and Trucharte C.Mitigating the pro － cyclicality of Basel II.Economic Policy，2010(10):661－702.

［20］Repullo R.and Saurina J.The countercyclical capital buffer of Basel III:a critical assessment.SSRN working paper，2011.

［21］Staiger D.，Stock J.H.and Watson M.W.How precise are estimates of the natural rate of unemployment?Reducing inflation:motivation and strategy.Chicago:University of Chicago Press，1997.

［22］Tarashev N.，Borio C.and Tsatsaronis K.Attributing systemic risk to individual institutions.BISworking papers，No.308，2010.

［23］Wells S.Financial interlinkages in the United Kingdom’s interbank market and the risk of contagion.The Bank of England’s working paper series，No.230，2004.