HTPB推进剂低温拉伸/压缩力学性能对比①
张晓军,常新龙,赖建伟,胡 宽
(第二炮兵工程大学,西安 710025)
0 引言
固体推进剂药柱是发动机结构的重要组成部分,在贮存和使用过程中,由于自重和内压等因素影响,同时承受多种载荷,表现出复杂的力学特性,直接影响其使用性能[1]。国内外研究人员采用理论和实验方法,从拉伸和压缩角度对推进剂的力学行为开展了大量深入的研究[2-4]。由于推进剂材料拉/压力学性能差异明显,而目前针对推进剂单轴拉伸和压缩两种状态力学性能对比研究较少[5],特别是针对低温条件下的对比分析尚未见公开报道,温度和应变率对推进剂拉伸和压缩性能影响的差异性并不清楚。因此,有必要进行相同温度和应变率条件下HTPB推进剂单轴拉伸和压缩力学性能对比研究。
本文开展了HTPB推进剂在不同低温和应变率条件下的单轴拉伸/压缩试验,对比分析了拉伸/压缩力学性能及其主曲线差异特点,并探讨了低温和应变率对力学性能拉压比值的影响,可为低温点火瞬态条件下固体火箭发动机药柱结构完整性分析提供参考。
1 试验内容
1.1 试样
HTPB复合固体推进剂的固体填充颗粒(AP/Al)质量分数为0.84,其他组分质量分数为0.16。根据QJ 924—85《复合固体推进剂单向拉伸试验方法》,将推进剂制成标准哑铃形试样用于单轴拉伸试验;制成φ20 mm×20 mm圆柱形试样用于单轴压缩试验。
1.2 试验方法
将试样放入设定温度的低温箱中保温1 h后,进行不同温度和应变率条件下的单轴力学性能试验,试验在电子万能材料试验机上进行,每个试验条件进行3组重复试验。试验温度分别为 25、-10、-20、-30、-40、-50 ℃,拉伸速率分别为 14、35、140、200 mm/min(1/300、1/120、1/30、1/21 s-1),压缩速率分别为 4、10、40、100 mm/min(1/300、1/120、1/30、1/12 s-1)。
2 试验结果与分析
2.1 低温拉伸/压缩应力-应变曲线对比分析
根据单轴试验结果,得到不同温度和应变率条件下推进剂应力-应变曲线,-40℃时推进剂的拉伸/压缩应力-应变曲线如图1所示。
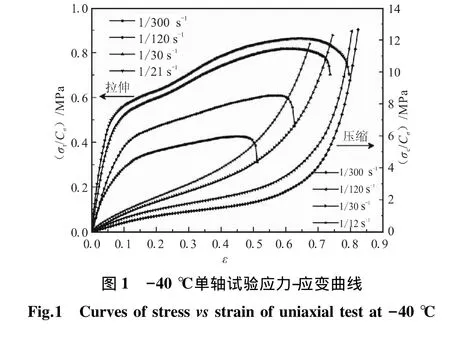
由图1可知,推进剂在-40℃拉伸/压缩时具有良好的粘弹特性,应力随着应变的增加逐渐增加,拉伸条件下前期应力增加较快,后期(应变高于10%)应力增加逐渐变缓直至破坏;压缩条件下前期应力增加较慢,后期(应变高于50%)应力增加较快,而且压缩应力显著高于拉伸应力。随着应变率的增加,最大抗拉强度和断裂伸长率逐渐增加。这是因为应变率越高,推进剂受载时间越短,内部裂纹没有时间发生扩展,推进剂仍能承受较大的载荷而不破坏,因而抗拉强度较大。而高应变率相对于低应变率时“脱湿”现象发生更少,载荷主要由推进剂基体承受,而且内部缺陷对高应变率不敏感。因此,高应变率条件下延伸率较大。由于相同原因,压缩条件下压缩强度随应变率的增加也逐渐增加,而由于压缩时没有最大载荷值,最大抗压强度和断裂伸长率无法准确衡量。
推进剂拉伸曲线表现出明显的弹性段、“脱湿”损伤段和破坏段3阶段变化规律,而推进剂压缩曲线只表现出明显的非线性,没有呈现出拉伸时的3阶段规律。为进一步分析压缩曲线特征,考虑压缩时的大变形情况,利用式(1)将工程应力转化为真应力进行处理,得到准静态压缩下典型真应力-应变曲线如图2所示。

式中 σ为真应力;F为加载力;S为试样的原始横截面积;ε为应变。

由图2可知,利用转折点A和B可将压缩真应力-应变曲线划分为弹性压缩、应力硬化和失稳破坏3个阶段,表现出和拉伸曲线类似的变形破坏过程。这是因为压缩过程中圆柱体试样周向承受拉伸载荷,最终失稳破坏是由周向拉伸载荷的纵向裂纹引起,这和推进剂拉伸具有类似性。为此,可参考推进剂单轴拉伸时力学参量的定义方法,将弹性阶段的线性段斜率定义为压缩模量,转折点B处的应力定义为压缩强度。
2.2 低温拉伸/压缩主曲线对比分析
推进剂在试验的低温和应变率范围内仍具有较好的粘弹性,符合时温等效原理,因而时间-温度移位因子 αT服从 WLF 方程[6-7]:

式中 C1、C2为材料常数,由试验数据拟合得到;T0为参考温度。
由式(2)可知,t=t0·αT,等式两边分别对 dε求导,整理得到代入式(2),可得:

式(3)反映了温度-应变率等效关系,移位因子αT与温度和应变率满足等式两边同取对数,得到:

根据试验数据,可得到不同温度和应变率条件下HTPB推进剂拉伸/压缩力学性能参量,参照 QJ 2487—93《复合固体推进剂单向拉伸应力松弛模量以及主曲线测定方法》,并结合式(3)和式(4),得到温度与移位因子lgαT的曲线和拉伸/压缩力学性能-温度-应变率主曲线,如图3和图4所示。

由图3可知,拉伸/压缩强度性能对应的WLF曲线基本重合,而模量性能对应的WLF曲线表现出较大差异,这说明温度和应变率对推进剂拉伸和压缩时的模量性能影响差异明显,而对强度性能影响相同,这为强度理论中一般采用强度比作为拉压特征值分析提供了理论依据[8]。通过图4可看出,拉伸力学性能主曲线的lg(αT·)相比于压缩主曲线较窄,而lg(αT·)反映的是温度和应变率范围,lg(αT·)范围越宽,说明可预测的应变率或温度范围就越宽。因此,不论是采用拉伸,还是压缩强度进行预测,其应变率范围较窄,参考温度下(25℃)应变率最大大约可预测至10 s-1,而采用模量进行预测则可达到 102、103s-1,对于常温低速拉伸预测能力则基本相同,达到 10-2.5s-1。由此可见,采用模量主曲线可对更高应变率的力学性能进行预测,相比于强度主曲线预测范围更宽。
根据图4中拉伸/压缩强度和模量与温度和应变率的关系,采用二次函数对其进行拟合,拟合结果见表1。

表1 不同温度下拉/压强度及模量与应变率关系Table 1 Relationships of tensile and compression strength and modulus with strain rate
由表1可知,拉伸/压缩主曲线关系式拟合相关性都较高,说明力学性能的温度和应变率效应都十分显著。主曲线关系式包含力学性能与温度和应变率的关系,利用主曲线关系式,可对不同温度和应变率条件下的力学性能进行预测,结合相关强度理论,可用于推进剂失效评价。
2.3 低温力学性能拉压比分析
相对于单一的拉伸或者压缩性能,拉压比可反映推进剂的抗拉和抗压能力的差异性。为此,选择相同温度(-50~25 ℃)和应变率条件下(1/300~1/30 s-1)拉/压试验结果用于对比分析,计算得到推进剂拉伸/压缩模量比(Et/Ec)和强度比(σt/σc)结果见表2。
由表2可看出,拉压模量比和强度比与温度和应变率条件有关,其值均小于1,说明推进剂在常温和低温条件下抗压能力较强,不易出现压缩破坏。拉压模量比大于强度比,在低温和高应变率条件下接近1,说明温度越低和应变率越高,推进剂拉伸和压缩模量越接近。随着应变率增加和温度降低,模量比和强度比没有呈现出规律性的变化趋势。
图4表明,推进剂拉伸/压缩强度曲线基本保持平行,而拉伸/压缩模量曲线相交,说明了温度和应变率对强度比和模量比的影响具有一定差别。为定量表征温度和应变率对强度比和模量比的影响规律,采用双因素方差分析方法对其进行分析。取显著性水平为0.05,方差分析结果见表3。其中,Fcrit为F统计量的临界值。

表2 拉伸/压缩模量比和强度比结果Table 2 Results of strength ratio and modulus ratio

表3 双因素方差分析结果Table 3 Results of variance analysis
由方差分析理论可知,F值大于Fcrit,说明因素对性能影响显著,反之影响不明显。由表3可看出,温度对应的模量比 F值(25.269)大于 Fcrit(3.326),应变率对应的模量比F 值(7.485)大于Fcrit(4.103),说明温度和应变率对模量比具有显著影响;温度对应的强度比F 值(4.493)大于 Fcrit(3.326),应变率对应的强度比 F值(0.87)小于 Fcrit(4.103),说明温度对强度比影响较大,而应变率对其影响较小。文中的模量比是指弹性模量比值,此时推进剂处于弹性段,并未发生损伤和破坏,其值与破坏行为关系较小,而主要由材料本身性质决定。温度越低,应变率越高,材料越硬,模量也就越大,但压缩不能与拉伸一起同步增长,导致拉压模量比变化较大。而推进剂强度除了与材料本身性质有关外,还与破坏行为有关。当推进剂受拉时,裂纹方向与载荷方向垂直,促进裂纹扩展;而推进剂受压时,周向载荷促进垂直裂纹扩展,轴向载荷却抑制水平裂纹的扩展。另外,温度和应变率还直接影响“脱湿”损伤的程度,会对拉伸/压缩强度造成显著影响,因而强度比表现出和模量比不同的变化规律。
3 结论
(1)推进剂在低温拉伸和压缩条件下,应力-应变曲线均表现出显著的3阶段变化规律,但其破坏机理有一定差别;
(2)拉伸/压缩模量主曲线比强度主曲线具有更强的预测能力,采用模量主曲线进行预测应变率可达到102、103s-1,比强度主曲线高出一个数量级。拉伸/压缩模量和强度主曲线拓宽了应变率和温度范围,均适合低温点火瞬态高应变率条件下推进剂性能预测和失效分析;
(3)低温对拉压强度比和模量比影响显著,应变率对模量比影响显著,而对强度比影响不明显,这与推进剂材料性能和破坏机理有关。
[1]侯林法.复合固体推进剂[M].北京:中国宇航出版社,2009.
[2]杨凤林,庞爱民,张小平.复合固体推进剂单向拉伸曲线分析[J].固体火箭技术,2001,24(3):54-57.
[3]王玉峰,李高春,刘著卿,等.应变率和加载方式对HTPB推进剂力学性能及耗散特性的影响[J].含能材料,2010,18(4):377-382.
[4]成曙,路廷镇,蔡国飙,等.含I型裂纹复合固体推进剂双轴拉伸实验研究[J].宇航材料工艺,2007(5):63-66.
[5]Ren Ping,Hou Xiao,He Gao-rang,et al.Comparative research of tensile and compressive modulus of composite solid propellant for solid rocket motor[J].Journal of Astronautics,2010,31(10):2354-2359.
[6]Radun J.Some aspects of time-temperature superposition principle applied for predicting mechanical properties of solid rocket propellants[J].Propellants,Explosives,Pyrotechnics,1999,24:221-223.
[7]Ho S Y.High strain-rate constitutive models for solid rocket propellants[J].Journal of Propulsion and Power,2002,18(5):1106-1111.
[8]强洪夫,曹大志,张亚.基于统一强度理论的修正M准则及其在药柱裂纹预测中的应用[J].固体火箭技术,2008,31(4):340-343.

