大功率全桥串联谐振充电电源理论设计

马 勋 ， 李洪涛

（1.中国工程物理研究院 流体物理研究所，四川 绵阳 621900；

2.中国工程物理研究院 脉冲功率科学与技术重点实验室，四川 绵阳 621900）

在脉冲功率技术领域，对初级储能电容常见的充电方式有恒压充电和恒流充电两种方式。前者基于大体积的工频变压器实现，常采用充电电阻限制充电功率，充电电阻消耗的能量为50%[1]；后者多采用全桥串联谐振充电电路，以“等台阶”升压方式实现对电容的恒流充电，具有体积小、效率高、功率密度大、适合宽范围变化的负载等优点，是较为理想的电容充电电源[2-5]。

构成全桥串联谐振充电电源的主要单元有：谐振电感和电容、功率器件、脉冲变压器。本文通过数值计算和模拟两种方法确定了这些单元参数的设计，并基于Pspice电路仿真软件对设计的全桥串联谐振充电电源进行了全电路模拟。

1 电路设计

全桥串联谐振充电电源由直流电源 V，逆变开关S1～S4，谐振电容 Cs和电感 Ls，变压器 TX，高压整流桥 D1～D4， 负载电容CL等组成，如图1所示。

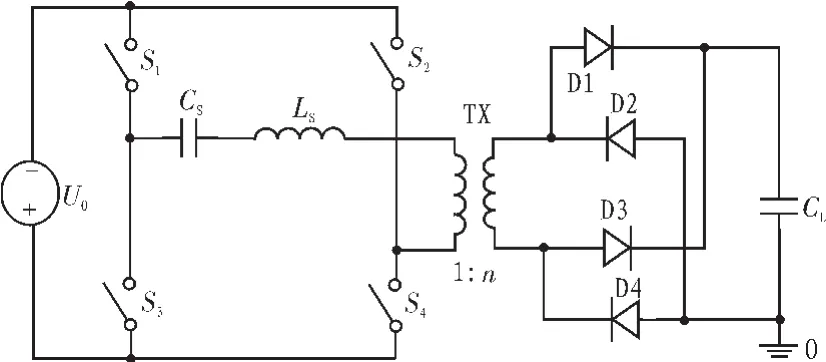
图1 串联谐振充电电路原理Fig.1 Schematic diagram of series resonant charge power supply

充电过程中，两组逆变开关 S1，S4和 S2，S3交替导通，完成一个开关周期。一个开关周期又可分为2个谐振周期，并根据逆变开关和高压整流二极管的导通情况分为4种工作模式，如图2所示。

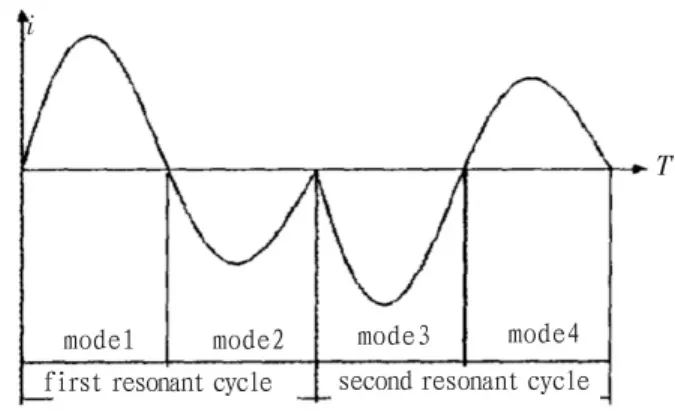
图2 串联谐振充电的初级电流波形Fig.2 Primary loop's current waveform of series resonant circuit

设计要达到的目标是对110 nF容值的负载电容充电至30 kV，充电重复频率1 kHz。逆变开关采用单只IGBT或其组件，从现有商业IGBT器件的经济性出发，逆变谐振重频设计为33 kHz。初级储能电容C0充电电压为1 kV。

1.1 谐振电路设计

调谐电容和谐振电感的计算分别如下[6]：

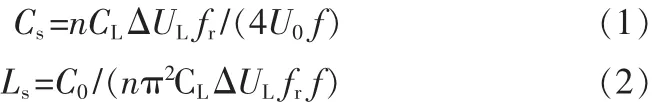
式中，Cs：调谐电容；n：脉冲变压器变比；CL：负载电容；ΔUL：每次放电负载电容电压降低值；U0：初级储能电容充电电压；fr：充电重复频率；f：谐振频率；Ls：谐振电感。

考虑到充电回路的电压效率损失，在设计时令初级充电电压U0=1.2 kV，每次放电ΔUL=30 kV。则计算出Cs=625 nF；Ls=37 μH；

1.2 功率器件设计

计算出通过IGBT组件的最大谐振电流和平均电流为：

则17个开关周期的时间约为：17×2T=1.03 ms，则充电周期接近1 kHz，满足设计要求。

1.3 脉冲变压器设计

脉冲变压器设计中，需要考虑的参数主要是[7]：伏秒数，励磁电感，漏感，耐压，功率。在本设计中，由于变压器初级输入电压为1.2 kV，次级期望输出电压达到36 kV，因此，变比设计为30。

在充电过程中，负载电容实质是一个变阻抗负载，随着充电电压增加，其阻抗不断降低，因此，变压器达到最大伏秒数应该在充电的后期。因此，伏秒数为：

V0T=1.2k×30.2 μs=36.24 mV.s （9）

在实际设计中，考虑一定裕量，伏秒数取45 mV.s。

由于负载阻抗不断变化，很难获得励磁电感和漏感计算的解析表达式，可采用数值模拟方法。忽略初次级绕组电阻，脉冲变压器以励磁电感和漏感等效[8]，则全桥串联谐振充电电源的等效电路如图3所示，其中L4为励磁电感；L3为折算后的次级漏感，其值为次级漏感的1/n2；C4为折算后的负载电容，其值为负载电容的n2，n=30。

Z：谐振回路阻抗。则：Z=7.69 Ω；Imax=312 A；Iavg=99.4 A。即选用的IGBT其耐压不应低于1.2 kV，峰值电流不低于300 A。

每一个开关周期，负载电容升压为：

计算出每个开关周期的ΔUe=1.8 kV，即总共需要17个开关周期才能将负载电容充至30 kV。

每个谐振周期为：

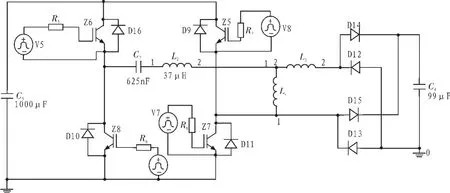
图3 谐振充电等效电路Fig.3 Equivalent circuit of series resonant charger

使用参数扫描的方法，先假定忽略次级漏感，令励磁电感的值分别为：10 μH，100 μH，1 mH，10 mH。 模拟结果如图4所示。

从图可见，当励磁电感值为1 mH，10 mH时，输出电压波形结果一致，而励磁电感为10 μH时，输出电压明显较低，说明励磁电感10 μH时变压器次级输出的脉宽和平顶度均不能满足要求。进一步模拟表明本设计所用变压器的励磁电感值不低于200 μH就可满足要求。对于磁芯变压器，该条件

容易满足。

1.4 散热设计

脉冲变压器的峰值功率为：

据此，计算获得Pmax=116 kW。平均功率为：

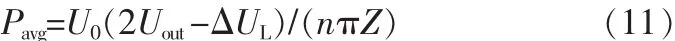
据此，计算Pavg=66 kW。但考虑到脉冲变压器工作时间短，仅几个ms，因此，变压器可不设计额外的散热装置。

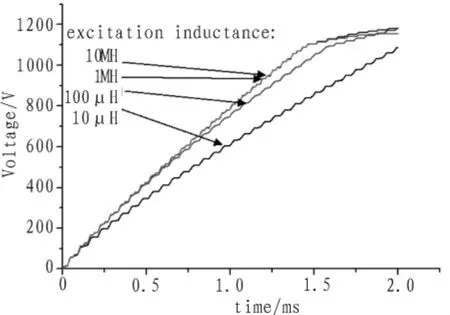
图4 不同励磁电感的输出波形Fig.4 Output voltage with different exciting inductances

2 电路仿真

根据以上设计参数，获得全电路以及仿真结果，分别如图 5，6。

根据模拟结果，电流谐振周期约30.2 μs，每个开关周期负载电压增量接近1.8 kV，则经历34个谐振周期，即1.03 ms后可完成对负载电容的充电，与设计预期一致。在对110 nF负载电容充电时，输出电压为等台阶，每个驱动电流半周期产生一个幅值1.8 kV台阶。

3 结 论

全桥谐振充电电源的谐振电感和电容决定谐振频率，功率开关的耐压和电流决定该器件的型号，脉冲变压器决定谐振功率脉冲高效率且低畸变地向负载传输，励磁电感和伏秒数是该脉冲变压器的最关键参数，脉冲峰值功率和平均功率参数决定散热系统设计。结合数值计算和模拟的方法[9]开展了全桥谐振充电电源的理论设计，确定了谐振回路的参数和脉冲变压器电感值，全电路仿真验证了设计的合理性，为该电源下一步实验工作奠定了基础。

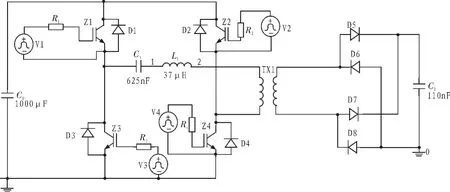
图5 设计的全桥串联谐振充电电源Fig.5 Circuit model of series resonant charging power supply

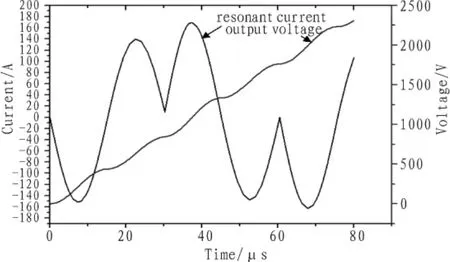
图6 全电路仿真结果Fig.6 Result of stimulant circuit

[1]刘锡三.高功率脉冲技术[M].北京：国防工业出版社，2005.

[2]Goebel D M.High powermodulatorforplasmaion implantation[J].Vacuum Science Technology，1994，12（2）：838-842.

[3]Kim J H，Rim G H，Jin H M.IGBT Stacks based pulse power generator for PIII&D [C]//IEEE Pulse Power Conf，2005:1012-1017.

[4]Rim G H，Kim T K.Semiconductor switch based pulse power generatorforPlasmasourceion implantation[C]//IEEE International Power Modulator Conference，2004:290-293.

[5]Rim G H，Kim T K.Solid state marx generator using series connected IGBTs[C]//IEEE International Power Modulator Conference，2004:567-571.

[6]苏建仓，王利民，丁永忠，等.串联谐振充电电源分析及设计[J].强激光与粒子束，2004，16（12）:1611-1614.SU Jian-cang，WANG Li-min，DING Yong-zhong，et al.Analysis and design of series resonant charging power supply[J].High Power Laser&Particle Beams，2004，16（12）:1611-1614.

[7]ZHANG Zhao，TAN Xiao-hua.Review of High Power Pulse Transformer Design[C]//18th International Vacuum Congress，2012:566-574.

[8]王瑞华.脉冲变压器设计[M].北京：科学出版社，1996.

[9]朱子勇，孙万民，王占林.某试验台LH2贮箱气体置换过程数值模拟[J].火箭推进，2012（4）：52-60，66.

ZHU Zi-yong，SUN Wan-min，WANG Zhan-lin.Numerical simulation of gas replacement process in LH2 tank of testbed[J].Journal of Rocket Propulsion，2012（4）：52-60，66.