多项式非负分拆算法的若干改进和补充
刘保乾
(西藏自治区组织编制信息管理中心,西藏 拉萨 850000)
0 引言
由文献[1-7]知,不等式自动发现与判定程序agl2012,能够通过输入简单且毫无联系的数据材料,自动发现三角形几何不等式、代数不等式、条件不等式(变元取值范围受限制或者给定约束条件)、四边形不等式等不等式类型,而且能够实现对多项式进行非负分拆,进而得到半正定多项式的配平方和.本文通过引入文献[8]中解线性方程组的算法和程序LPSOLVE,对agl2012程序的非负分拆模块agl2012_lsos进行改进和补充,从而进一步完善了程序的功能,拓宽其应用范围,同时将改进后的程序模块升级为新版本,即agl2013_lsos.
1 多项式非负分拆的数据构造及程序
多项式非负分拆,或者配平方和的数据构造有两方面的含义,其一是构造分拆项集合;其二是构造分拆表达式,不同的构造方案将决定分拆的成败及分拆结果的形式.在基于文献[8]程序LPSOLVE的情况下(而不是文献[7]中的随机数验证程序),多项式非负分拆的主要算法便集中在数据的组织和构造上.下面介绍三种数据构造方案:
1.1 数据构造方案A
3元多项式f(x,y,z)的分拆项一般式可表示为g(x,y,z)(h(x,y,z))2的形式,文献[7]中的注7称h(x,y,z)为基本对称项,为了叙述方便,这里称h(x,y,z)为基本项,称g(x,y,z)为附加项.由此可知分拆项是由基本项和附加项相乘得到的,基本项决定分拆项的基本形式和特征.显然多项式f(x,y,z)和基本项h(x,y,z)以及附加项g(x,y,z)的次数应满足等式

其中∂f表示f的次数.式(1)是构造分拆项的基本关系式.对分拆项取和即可得到分拆表达式.
为了省去大量的叙述,这里通过对程序作注释的办法来说明数据构造方案A.构造3元4次分拆项集的主要程序段如下:
temp:=lbxcun(zzz(0),cf(d1c(qd,sx),4));
temp:=temp union lbxcun(zzz(2),cf(d1c(qd,sx),2));
temp:=temp union lbxcun(zzz(0),cf(d2c(qd,sx),2));
temp:=temp union zzz(4);
temp:=bc3g(temp);
temp:=glcs(temp);
在上述程序段中,cf(d1c(qd,sx),4)表示一个基本项,其中d1c(qd,sx)表示一个系数在[qd,sx]内取值的一次式,cf(f,n)表示对f进行n次方,故cf(d1c(qd,sx),4)的次数是4,zzz(0)表示一个次数是0的附加项,lbxcun是数据运算命令,表示两个集合中的元素依次相乘,这样表达式lbxcun(zzz(0),cf(d1c(qd,sx),4))的运算结果是一个4次分拆项.
类似,表达式lbxcun(zzz(0),cf(d2c(qd,sx),2))也表示一个4次分拆项,只不过此时基本项是一个二次式的平方而已,注意d2c(qd,sx)得到的是一个系数在[qd,sx]内取值的二次式.
bc3g的含义是"变成3个",即根据对称性,由一个分拆项p(x,y,z),得到另外两项p(y,z,x)和p(z,x,y).
glcs的作用是过滤掉分拆项前面的常数.
语句temp:=factor(temp)的作用是过滤掉集合中等价的重复项.
例1 试写出系数在[-1,1]内取值的3元3次分拆项集合.
解 在Maple环境中,在读入agl2013_lsos程序的情况下,键入命令zgc3(-1,1),立即输出由40个分拆项构成的集合:
{y(x+y-z)2,z3,y(y-z)2,y(z+x)2,y(y+x)2,…,x(x-z)2,xz2}.
1.2 数据构造方案B
在数据构造方案A中,如果将语句cf(d1c(qd,sx),4)改为
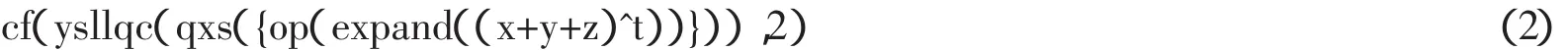
则可得到数据构造方案B,具体含义是(这里取t=3):
a.展开(x+y+z)3,并将展开式中的各单项式前的系数变为1,并置入一个集合,得
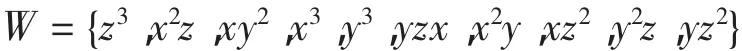
b.对W集中的元素作给定的运算S(这里取S为W中元素两两取差),并平方得
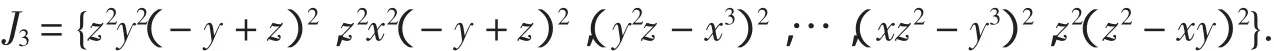
c.改变(2)式中的t值,并重复a-c过程,从而得到集合Jt(t=1,2,3,4,…).
d.取不同的t值,并将得到的Jt进行相乘(目的是为了得到交叉项),再将相乘结果相并,得到分拆项总集合.
根据分拆需要,还可将运算S取为其他特定的运算,从而得到更庞大的分拆项集合.
注1 在数据构造方案B中,得到的分拆项总集合中各元素的次数是不相等的.
1.3 数据构造方案C
在方案C中,n次分拆项集W可由两部分构造:一是由分拆项通式
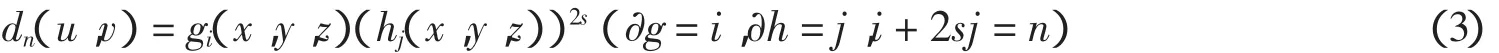
直接构造n次分拆项集D,在(3)式中u,v表示基本项hj(x,y,z)的系数取值范围是[u,v];二是由诸次分拆项集D相乘构造分拆项集Q,Q的构成公式是
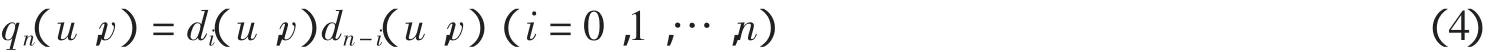
D和Q相并即得到n次分拆项集W.
方案C的优点是由公式(4)可以产生丰富的交叉项,且构造方案与系数范围[u,v]有关,这使得数据覆盖面大大拓广了.
在agl2013_lsos程序中,主要的分拆项集构造命令有zgc,zll以及scd等,还有一些预先计算出来的分拆项库(为了节约时间),几乎每一个分拆操作都要涉及到这些构造命令.
2 agl2012_lsos程序改进的若干思路和途径
除过上述数据构造方案外,agl2013_lsos的主要算法还体现在下面的思路和途径中:
1.没有零点(1,1,…,1)的多项式非负分拆.要实现没有零点(1,1,…,1)的多项式非负分拆,只要保证分拆项集合中含有正的分拆项即可.其实,agl2012_lsos程序中的ak_3y系列命令已经能够对没有零点(1,1,…,1)的多项式进行非负分拆,其依据是文献[7]中的算法lsos_zj和lsos_bd,但其分拆效率不高;而对对称式和轮换对称式,由于将分拆表达式设为
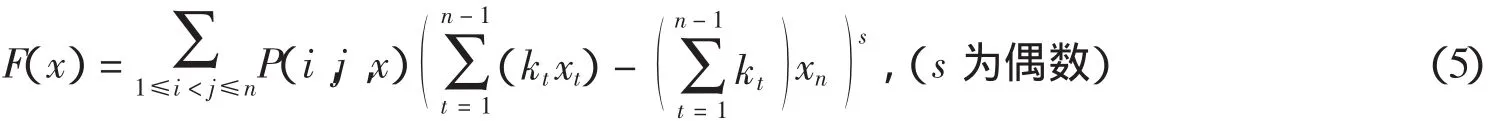
的形式,故由文献[7]中的算法lsos_pf(相应命令是dca)不能分拆没有零点(1,1,…,1)的多项式.其实,对对称式和轮换对称式,可将分拆表达式(5)改为一般式

这样就可以分拆没有零点(1,1,…,1)的多项式了,而且这样做就完全兼容了文献[7]中的算法lsos_pf.而对不对称式,按文献[7]中的算法lsos_dxs,把分拆项集中的每v个元素分成一组,但不再做多项式线性无关性检验,而直接调用文献[8]中解线性方程组的程序LPSOLVE进行求解.为了能够保证尽可能的有分拆解,v的值要取的足够大,甚至可以用整个分拆项集建立分拆表达式,这样做的好处是可靠,缺点是效率低下,且结果可能会很复杂.
2.为了提高分拆效率,减少无效分拆项,可用随机数验证程序对分拆项集进行过滤.过滤的依据是:如果e是多项式f的分拆项,则存在正数k使不等式f≥ke成立.
3.当分拆项集中的元素较多时,可采用如下算法:先取出分拆项集中两个元素构成分拆表达式,如果拆不出,则再取出1个元素进行分拆,以后每次增加一个元素,直到拆出,或者将分拆项集中的元素全部用完为止.这是一个较为实用的分拆算法.
4.对一个分拆项集,可尝试对变元作特定的代换,如作代换x→y+z,y→z+x,z→x+y等,从而得到新的分拆项集.将新的分拆项集与原来的分拆项集相并,这样可以扩大分拆范围.
5.文献[8]中的LPSOLVE是一款方便实用的求方程组正解的程序,但是它还是受变量数目限制的.为了解决这个问题,一个可行的办法就是对分拆项集进行分块.不同于文献[7]的分块策略,本文采用按分拆项字符长度进行分块,这不仅提高了分拆效率,而且还由于分拆项字符长度相同,分拆出的结果更简洁工整.在分拆程序设计中,还可对诸分块进行组合,从而得到更加丰富多彩的分拆结果.
6.另一个解决LPSOLVE受变量数目限制的办法是对分拆项集进行随机过滤,其算法是:先计算出分拆项集W的元素数目n,用n去除一个随机数得到一个在[0,n-1]内取值的余数i,以i作为下标取出W中的一个元素W[i],这样就过滤出了分拆项集W中的一个元素W[i].将这样的过滤共进行n次,就得到W的一个随机过滤集.由于每次过滤时得到的元素下标可能相同,这样能够保证随机过滤集总是的W的真子集,从而达到简体计算的目的.主要语句是:for i to gs do if gs>1 then temp:=`union`(temp,{ex[irem(rand(),gs-1)+1]})end if end do.
依据上述算法和思路,可以对agl2012_lsos程序进行一系列改进,从而得到若干agl2013_lsos新命令.限于篇幅,下面仅举一例.
例2 设x,y,z≥0,t≤2证明不等式(以下用∑表示循环求和)
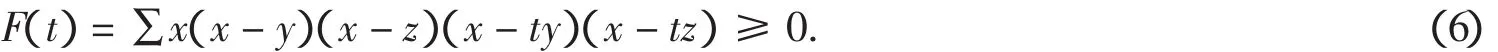
证明 用dca命令易得
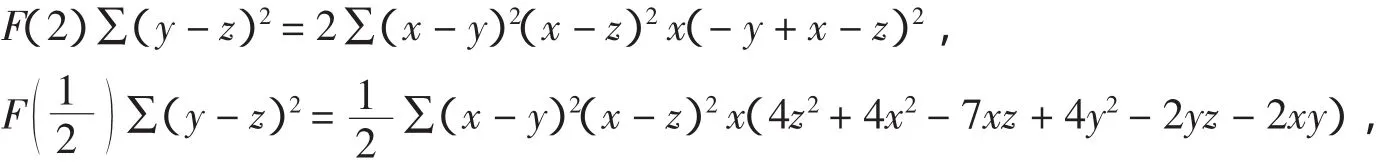
根据这个分拆结构,用待定系数法易得恒等式
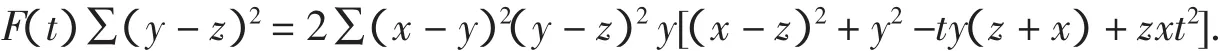
显然当t<0时F(t)≥0成立.当0 把实系数半正定齐次多项式表示为实系数齐次多项式的平方和,通常称为SOS[9].通过两种方式可以实现半正定多项式的SOS表示:一是直接构造多项式完全平方型分拆项集,以分拆项集中的元素构造分拆表达式,然后调用文献[8]的LPSOLVE程序进行求解.这种情形比较简单,这里不做详细讨论.二是构造SOS型分拆式,然后对分拆式待定求解.下面以3元多项式为例说明第二种方法. 一般情况下,3元多项式f的分拆项表达式可表示为: 的形式,其中(gc_ex(2,t,[x,y,z]))^2是基本项,gc_ex(1,degree(f)-2*t,[x,y,z])是附加项,gc_ex是表达式构造命令[7].由于基本项已经是一个完全平方因式,故要得到SOS表示,必须保证附加项gc_ex(1,degree(f)-2*t,[x,y,z])中各单项式的变元为偶次方,为此,要将gc_ex命令改进为zzr函数,即分拆项通式要写为: zzr((n-2*t)/2,i)*(gc_ex(2,t,[x,y,z]))^2 的形式,函数zzr的作用是产生一个不含变元奇次方项的附加式.为了直观说明构造过程,先看一下zzr函数的运行效果: 命令zzr((6-2*1)/2,1)*(gc_ex(2,1,[x,y,z]))^2的执行效果是: 命令gc_ex(1,6-2*1,[x,y,z])*(gc_ex(2,1,[x,y,z]))^2的执行效果则是 可以看出,zzr函数已经达到了设计要求.限于篇幅,zzr函数的具体设计思路此略. 注2 为了拆出含有负系数的分拆项,可将zzr函数改进为zzr_c函数,zzr_c的功能是可在附加项中增加一些完全平方项,如键入zzr_c(1,1)命令可输出: 在实际编程时可将zzr_c函数与过滤字符长度函数glcd结果起来,也可与随机数函数rand结合起来,从而做到附加项中完全平方项的灵活选取. SOS表示程序的设计关键是构造完全平方型分拆项集,下面以3元4次为例说明分拆项集的构造过程.有关程序模块和主要语句如下: a)bd1:=rgc2(qd,sx); b)bd0:=lbxcun(bd1,bd1); c)temp:={}; d)for k11 from qd to sx do… e)for k16 from qd to sx do f)temp:=temp union{(k11*x^2+k12*y^2+k13*z^2+k14*x*y+k15*x*z+k16*y*z)^2}od od od od od od; g)temp:=temp union bd0; h)temp:=temp union bd1 minus{0}. 语句a)是构造3元2次分拆项集,主要由集合{x2,y2,z2}和集合{(ix+jy+qz)2}相并而成;语句b)将两个3元2次分拆项集中的元素相乘,其中lbxcun是数据构造命令;语句c)到f)产生由表达式(k11x2+k12y2+k13z2+k14xy+k15xz+k16yz)2决定的分拆项集;语句g)和h)将各次集合相并得到总集合temp.按照这个程序模块的思想,可以构造更高次的分拆项集合. 很显然,这里构造的分拆项集合中的元素次数是不相等的.为了用temp集合中的元素表示出多项式expr,需要运行如下程序模块: 1.n:=degree(expr); 2.temp1:=0; 3.forifrom 1 to nops(temp) do 4.ifdegree(temp[i])<=degree(expr)then 5.temp1:=temp1+temp[i]*zzr((n-degree(temp[i]))/2,i) end ifod; 6.yan:=temp1; 7.ex-yan; 8.collect(%,[x1,x2,x3],distributed,factor); 9.{op(subs(x1=1,x2=1,x3=1,[op(%)]))}; 10.ls:=solve(%); 11.iffactor(subs(ls,yan)-ex)=0 then 12.var:=indets(ls); 13.je:=lpsolve(ls,var); 14.ifje<>{}then dtm:=subs(je,yan);jg:=jg union {dtm} end if end if; 其中语句3-5根据分拆项集temp中元素的次数构造多项式expr的分拆表达式,如果分拆项temp[i]的次数大于多项式expr的次数,则为无效分拆项,此时temp[i]不参与构造,否则temp[i]将与zzr函数结合,产生形如(9)式的表达式,最终得到分拆表达式yan;语句6-12完成待定求解;语句13调用LPSOLVE解方程组,最后完成分拆.不同次的分拆项构成分拆项集合,这为分拆各种可能的复杂情形提供了便利.据此思路就可以得到相应的SOS表示命令. 例4(文献[9])试将f=x4+2x2y2+x3z+z4表示为SOS. 解 键入命令bqrj4r(-1,1,f),很快输出100多个结果,其中较简洁的是 例5 设x,y,z∈R,证明不等式(http://www.aoshoo.com/bbs1/dispbbs.asp?boardid=48&id=23707&page=1&star=1) 证 不等式(10)是文献[10]中的例4.文献[10]两次用ak_3y命令得到分拆结果,现用agl2013_lsos命令进行新证:键入realh(f,16)命令,直接输出分拆结果 对称多项式SOS表示的另一个算法是用dca命令,即用dca命令得到普通平方分拆,然后用实数反例库lsos_3y_tfx_cs_r对分拆项中的附加项进行测试,如果附加项当变元为实数时非负,则对附加项进一步调用相关程序做SOS分拆,由于与原多项式相比已经降低了次数,故这种算法效率还是比较高的.具体例子此略. 设ΔABC三边为a,b,c,构造锐角三角形不等式分拆项集,要注意其数据特征是 用此特征不论是构造分拆项集还是构造分拆表达式,均容易实现分拆,此不详述. 例6 在锐角ΔABC中,证明不等式f=a3+b3-c3+ac2>0 证 键入命令bqrj3(-1,1,f),很快输出一批分拆结果,现选出其中的一个: 文献[11]提出了智能模拟的概念.智能模拟就是尽可能多地把人的探索行为及推理过程用机器全部或部分代替,以提高效率,减少低级重复劳动,在一个较高的起点上使用数据和材料,发现研究线索和规律.下面以自动发现多项式不等式并配平方和为背景,设计2个智能模拟案例. 例7 试设计一个不等式发现器及处理程序,它能够自动输出3元4次多项式不等式,对输出的不等式能够配出平方和,并将不能配出的多项式置入一个集合. 解 通过以下3步可以完成题目所给的任务:1.发现器的设计.由gc_ex命令建立表达式然后取系数变化范围为[-1,1]建立循环程序,对每一个具体的多项式,调用文献[2]中的随机数验证程序进行非负性测试,从而得到一个自动发现器. 2.对发现结果进行处理.由于最初的发现结果往往比较粗糙,其中有不少是平凡的,这样就需要设计若干个过滤器,以得到高品质的研究材料.另外,大量的发现结果中隐藏着一些特殊性质的多项式(如零点特性,差分代换特性等),对这类多项式也需要用过滤器进行挑选.对于多项式不等式,常见的过滤器有: (1)完全平方过滤器.这类多项式显然是没有意义的,需要过滤掉.主要通过Maple的op命令和type命令实现. (2)结果表达式字符长度过滤.在众多的发现结果中,如何把最简洁的结果挑选出来?此时就要用到此过滤器.主要实现命令是maple的length函数. (3)过滤常数.自动发现结果中往往混有一些常数,此时需要过滤掉,主要用Maple的indets函数,语句是if indets(expr[i])<>{} then temp:=temp union{expr[i]}end if. (4)过滤字母.简单,略. (5)过滤有零点(1,1,1)的多项式.此设计简单,略. (6)按对称性进行过滤,用symmfunc命令实现. (7)过滤只含有一个负系数项的多项式. (8)过滤有特殊零点多项式,如x=y=kz时取值为零的半正定3元多项式. (9)过滤等价式,此略. (10)过滤二次函数.自动发现结果中,有些以某变元整理可得到一个二次函数,有时需要把这类多项式挑出来(如编写竞赛题目),此时就需要此过滤器. (11)过滤系数全部为正的多项式.如果多项式系数全部是正数,则显然是平凡的,此时就需要过滤掉,用has(-1,map(signum,[coeffs(expand(ex[i]))]))等命令即可实现. (12)过滤差分代换不终止者.一些多项式用逐次差分代换[12]方法证明时不终止,这类多项式往往有比较特殊的性质.对变元较少的多项式,可用文献[13]中的差分代换及公式设计过滤器. (13)过滤Si类多项式[14]. (14)随机过滤命令.以随机方式减少分拆项集,以解决LPSOLVE程序对方程组变元个数的瓶颈,实现分拆结果的随机输出.在分拆高次多项式时,由于分拆集十分庞大,此时可采用随机过滤命令叠套的方式进行过滤. 经过以上过滤器过滤后,就可实现自动发现结果的分类输出. 3.配平方和.对自动发现的多项式,用本文中的配平方和命令逐个检验,能够配出来的就直接显示,不能够配出的置入一个集合变量之中.对于不能配出的多项式有两种情况:要么是由于程序功能局限不能配出,要么是多项式本身就不能表示为SOS.不论何种情况,都为进一步研究提出了努力方向. 例8 如果3元多项式f(x,y,z)取值为零的条件是x=y=z和x=uy=vz(u,v不全为1),或者这些条件式的轮换,则称f(x,y,z)是3元扩展S类多项式;如果满足u≠v≠1,则称f(x,y,z)是3元非平凡扩展S类多项式.试寻找若干3元4次非平凡扩展S类多项式. 解 键入以下命令: >d:=map(sgm,qxs({op(expand(sgm(x)^4))})); >temp:=0;for i to nops(d) do temp:=temp+k||i*d[i]end do; >solve(subs(x=1,y=1,z=1,temp),k5); >dd:=subs(k5=-k1-k2-k3-k4,temp); >ls:=solve(factor(subs(x=u*y,y=v*z,dd)),k4); >bd:=subs(k4=ls,dd); >jg:=subs(u=2,v=4,bd);#给u,v赋具体的值; >jjg:=fxb(-100,100,jg);#fxb是agl2012程序的自动发现命令; 则程序运行2个多小时后输出(如果取参数为200,则运行时间是53 742.189秒) 故不等式(12)成立,此不等式取等号的条件是 此条件可化为{x=3y,z=6y},{y=y=z}及其轮换,故f1是一个半正定扩展S类多项式.另外,由上述发现不等式(12)的命令序列可知,不等式(12)的另一个取等号条件是{x=2y,y=3z}. 在上述命令中,不断改变u,v的值,可找到其他的扩展S类多项式,如 就是一个半正定扩展S类多项式. 接触过agl2012或者agl2012_lsos程序的用户可能会有一个很深的印象:就是程序有太多的命令.为什么会出现这种情况?主要原因是:我们的程序是一个验证程序,只能通过一些特殊情形来对付一般,这样每一个具体的命令就只能解决某种特定范围内的问题,对另一些问题可能就无解.为了解决这个问题,可以设计若干自助命令,同时给出自助命令具有的一般性规则或使用方法即可,这样就可以根据具体的问题设定解决的条件和范围.下面介绍一组自助命令,这些自助命令的使用格式是:命令保留字(分拆项集,欲分拆多项式). 例9 (http://www.artofproblemsolving.com/Forum/viewtopic.php?f=52&t=516785&p=2910105#p2910105)证明不等式. 解 由于f是4次式,故可采用诸次分拆项集相乘的办法构造数据: >dat2:=ezgc2(-2,2);#构造2次分拆项,系数范围取为[-2,2]# >dat4:=ezgc4(-1,1);#构造4次分拆项,系数范围取为[-1,1]# >qd:=lbxcun(dat2,dat2);#2次分拆项集中元素自乘,以产生与f对应的4次数据# >jg4:=qd union dat4;#两个4次分拆项集相并# >lpsolve_e(jg4,f);#调用自助命令求解# 则很快输出分拆结果f=4x(2x-1)2+(x2-1+x)2+4x2(2x-1)2. 自助命令的好处是明显的:当我们得不到解时,可以对设定的数据范围进行调整,直到解决问题为止(如上述数据准备过程中完全可以考虑ezgc1(-2,2)和ezgc3(-2,2)相乘产生的4次分拆项集),这种对用户开放的使用形式,无疑可以弥补程序算法的不足或缺陷. 在agl2013_lsos程序中,自助命令还有elpsolve,lp_c等,这里不再举例了. 本文对agl2012_lsos程序模块进行了若干改进,扩大了程序的功能和应用范围.尤其是引入了文献[8]中的解线性方程组命令LPSOLVE,使程序运行效率大大提高.反观文献[7]、文献[8]和本文,我们有如下体会和认识: 1.由文献[7]知,随机数验证程序是多项式非负分拆的一个支撑;由文献[8]及本文知,解线性方程组的高效算法LPSOLVE是另一个支撑.事实上,本文新增的许多命令调用了LPSOLVE程序.文献[15]中的例11表明,得到一个多项式的平方和表达式是容易的,但要得到它的一个具体分拆解却有一定困难,原因就是因为当时没有象LPSOLVE那样的解线性方程组的算法和程序,也没有随机数验证算法和程序. 2.LPSOLVE程序得到的是系数全部为正数的分拆式,而用随机数验证程序可以得到含有负系数项的非负分拆式.对于高次的对称式或轮换对称式,可先用dca等命令降次,然后再调用本文的有关分拆命令,这样做可以提高分拆效率.有些问题用随机数验 而用本文中与LPSOLVE有关的命令却未能够做出.所以说LPSOLVE算法和随机数验证算法的结合和互补是很有必要的. 3.笔者在测试过程中发现一些情况下LPSOLVE会出现死循环不出结果,建议在LPSOLVE中设置时间开关,这样可以保证在批量验证中保持自动性和连续性. 4.由网站http://www.aoshoo.com/bbs1/index.asp?boardid=48上的系列贴可以看出,不等式自动发现与判定程序agl2012发现的各次多项式不等式,不论对完善本文中的算法还是对完善LPSOLVE程序均起到了有益的促进作用. 5.本文例8提出的扩展S类多项式,可以看作是S类多项式的推广,是一个十分重要的多项式类型,它和Si类多项式一样,都有特殊的零点.由于半正定非平凡扩展S类多项式的分布似乎更加稀少,这使人们对它的性质了解更少,尤其是3元以上的非平凡扩展S类多项式目前还未找到实例.希望有更多的人关注扩展S类多项式尤其是4元以上的扩展S类多项式的研究. 最后提1个待解决的问题:如何对涉及两组变元的多项式进行平方和分解?这对解决涉及两个三角形不等式的一类问题是很有意义的. [1]刘保乾.三角形不等式判定程序agl2009的改进及应用[J].佛山科学技术学院学报:自然科学版,2011,29(1):24-32. [2]刘保乾.不等式的自动发现原理及其实现[J].汕头大学学报:自然科学版,2011,26(2):3-11. [3]刘保乾.不等式自动发现和判定程序agl2010的若干改进及应用[J].广东教育学院学报,2011,31(3):13-22. [4]刘保乾.再谈不等式自动发现与判定程序agl2010的改进和应用 [J].汕头大学学报:自然科学版,2012,27(1):14-23. [5]刘保乾.用agl2010程序研究涉及两个三角形的不等式[J].佛山科学技术学院学报:自然科学版,2012,30(2):11-21. [6]刘保乾.四边形不等式的自动发现[J].汕头大学学报:自然科学版,2012,27(2):9-17. [7]刘保乾.随机数验证程序在多项式非负分拆中的应用[J].汕头大学学报:自然科学版,2012,27(3):27-37. [8]隋振林.一个求线性方程组非负解的通用程序[J].广东教育学院学报,2013,33(3):In press. [9]李轶.一类半正定多项式的配平方和算法[J].系统科学与数学,2008,28(4):490-504. [10]刘保乾.一些常见不等式的配平方和[J].不等式研究通,2012,19(1):49-58. [11]刘保乾.用不等式自动发现和判定程序agl2010的研究n元不等式 [J].广东教育学院学报,2012,32(3):13-21. [12]杨路.差分代换与不等式机器证明[J].广州大学学报:自然科学版,2006,5(2):1-7. [13]刘保乾.再谈第二类差分代换[J].佛山科学技术学院学报:自然科学版,2009,27(2):25-30. [14]刘保乾.类多项式初探[J].广东教育学院学报,2007,27(5):6-13. [15]刘保乾.多项式的一般表示式及其应用[J].广东教育学院学报,2010,30(3):17-24. [16]徐国辉,舒红霞.分式不等式中的"四朵金花"[A].见:杨学枝编,不等式研究(第2辑)[C].哈尔滨:哈尔滨工业大学出版社,2012:189-192.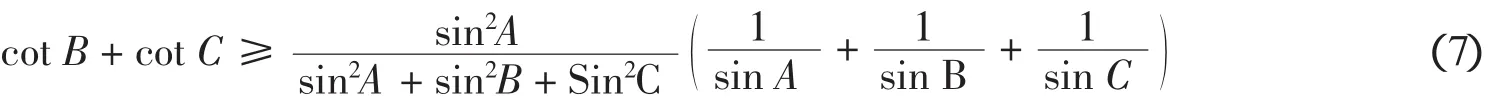
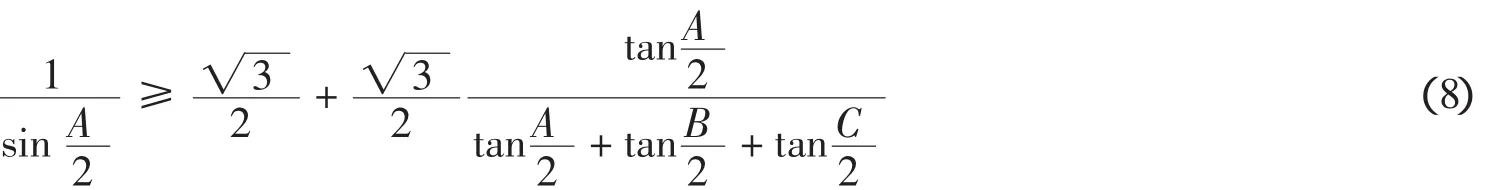
3 寻求多项式的SOS表示
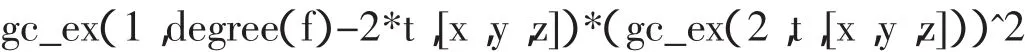
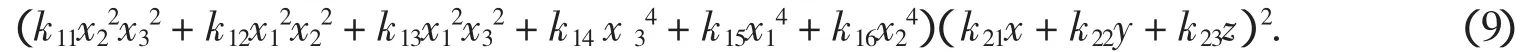
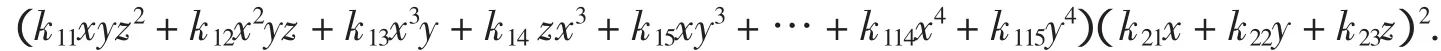
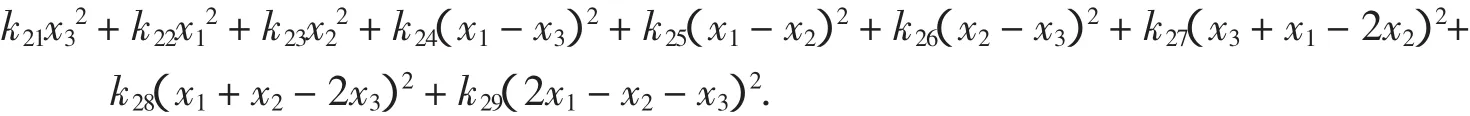
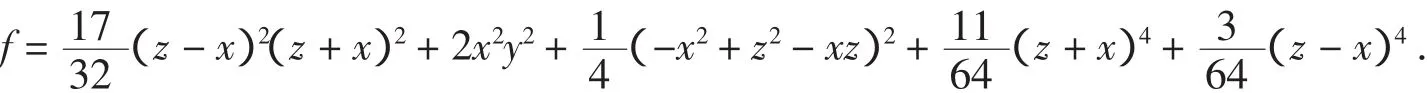
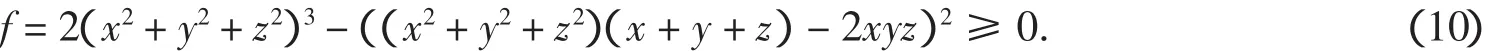
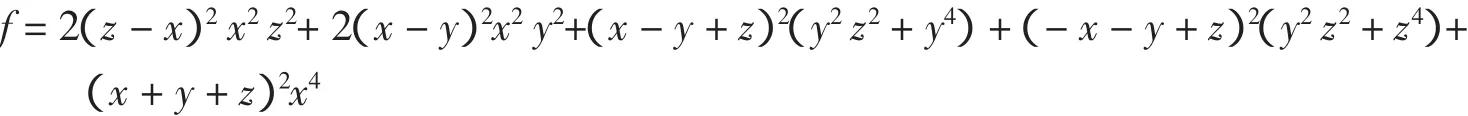
4 锐角三角形不等式的分拆证明
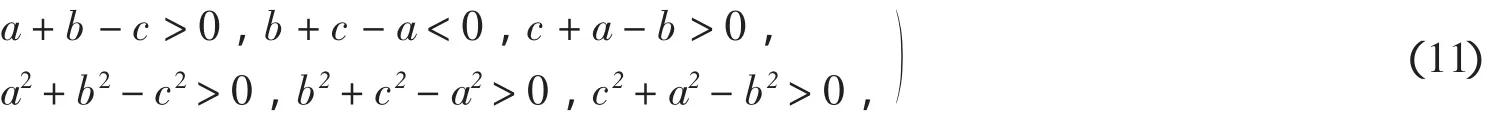
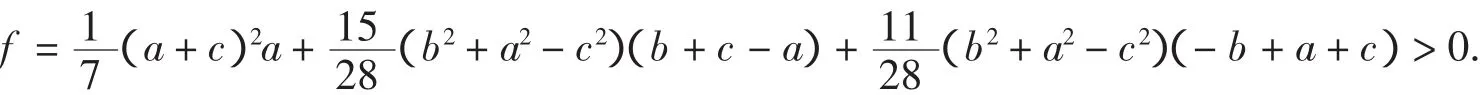
5 智能模拟的2个案例
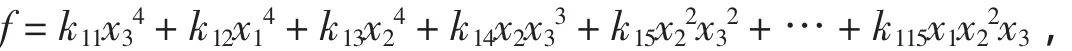
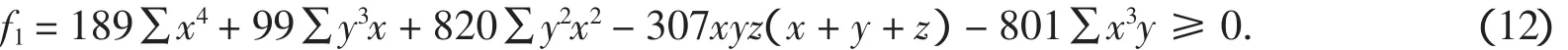
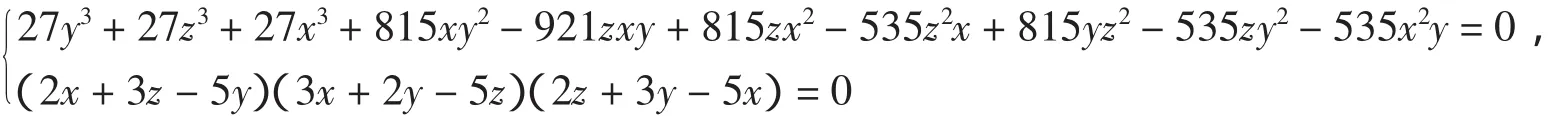
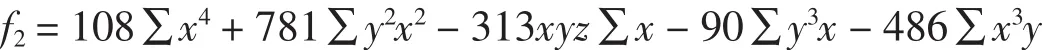
6 自助命令
7 结语和问题

