高含水期油田水驱特征曲线关系式的理论推导
宋兆杰,李治平,赖枫鹏,刘刚,甘火华
(1. 中国地质大学(北京)能源学院;2. 延长石油集团研究院;3. 中国石油天然气勘探开发公司)
0 引言
水驱特征曲线可以根据油田累计产油量、累计产水量、累计产液量及水油比等生产数据有效预测油田可采储量,在国内油田中得到广泛应用。目前水驱特征曲线多达数十种,常用的主要有甲型、乙型、丙型和丁型4种,陈元千[1]和俞启泰[2]从不同角度完成了对上述曲线关系式的理论推导,另外张金庆[3]推导出了适用范围更广的水驱特征曲线。实际应用发现,水驱特征曲线在油田开发后期常表现出上翘现象,针对这一问题,陈元千[4]基于油水两相流动基本原理,推导认为甲型、乙型水驱特征曲线在开发后期存在第 2条直线段,并提出甲型和乙型水驱特征曲线的第 2种表达式。从实际应用看,由于不同方法的理论基础不同,预测的可采储量数值明显不同。一般认为,甲型和丙型水驱特征曲线预测结果较为可靠,丁型水驱特征曲线结果明显偏高[5]。不同开发阶段预测可采储量使用的方法原则上应该具有一致性,以便分析对比,同时应选择与生产动态较吻合的计算结果,而不能把所有方法计算结果的平均值作为标定值。
在前人研究的基础上,本文分析了常用水驱特征曲线的适应性,重点研究了油水相对渗透率比(Kro/Krw)与含水饱和度(Sw)在半对数坐标中的直线偏移段,拟合适合高含水阶段的Kro/Krw-Sw关系的新型表达式,推导出新型水驱特征曲线关系式。实例分析表明新表达式计算简便可行,对高含水期油田水驱评价方法发展和完善具有一定意义。
1 水驱特征曲线方法评价
表 1是常用水驱特征曲线表达式和水驱可采储量预测表达式。水驱特征曲线法一般通过拟合直线段进行可采储量标定,因此确定直线段起始点是方法应用的关键。普遍认为当油田含水率超过 50%之后,不同方法都能出现直线段[6]。为了使水驱特征曲线方法的应用规范化,文献[6]中提出油田开发过程中每次进行可采储量标定应保持直线段起始点不变,避免出现预测可采储量由大变小的现象。

表1 常用水驱特征曲线及水驱可采储量表达式
传统水驱特征曲线推导的假设条件是在油、水两相渗流条件下,中含水阶段Kro/Krw与Sw呈半对数直线关系[7],即:

在油田开发后期,水驱特征曲线常出现上翘现象。文献[8]利用流管法计算并绘制的水驱特征曲线(见图1)呈现出后期上翘特征。假定极限水油比为49,应用乙型水驱特征曲线计算的理论可采储量比实际可采储量明显偏高,因此对于高含水期油田,不能直接应用传统方法。
2 高含水阶段Kro/Krw-Sw新型关系式
(1)式描述的 Kro/Krw与 Sw关系在中含水阶段具有很好的代表性,但在高含水阶段曲线明显偏离直线,导致(1)式无法准确表达二者的关系[4,9]。本文利用大庆贝尔油田某区块8块岩心和榆树林油田东14区块5块岩心相对渗透率数据资料,应用平均相对渗透率方法[10]分别进行归一化处理,并借鉴长庆西峰油田庄19井区[11]岩心数据(见表 2),绘制出 Kro/Krw随 Sw变化的半对数曲线(见图2)。
由图2可以看出,在高含水阶段,Kro/Krw-Sw曲线均不同程度地偏离半对数直线关系。为推导高含水期油田水驱特征曲线关系式,对图 2中高含水阶段曲线偏移段进行拟合(见图3),并回归得到Kro/Krw-Sw的新型关系式(见表3)。
由图3和表3可知,应用二项式拟合高含水阶段ln(Kro/Krw)与Sw关系式吻合度很高,表明应用二项式可以更加准确地描述高含水阶段 Kro/Krw与 Sw的曲线关系,即:

为便于直观认识和公式推导,将(2)式转化为:
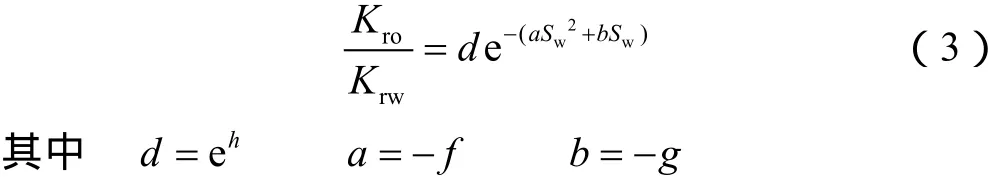
可以看出,本文推导的高含水阶段 Kro/Krw与 Sw关系式((3)式)与中含水阶段关系式((1)式)有较大差异。
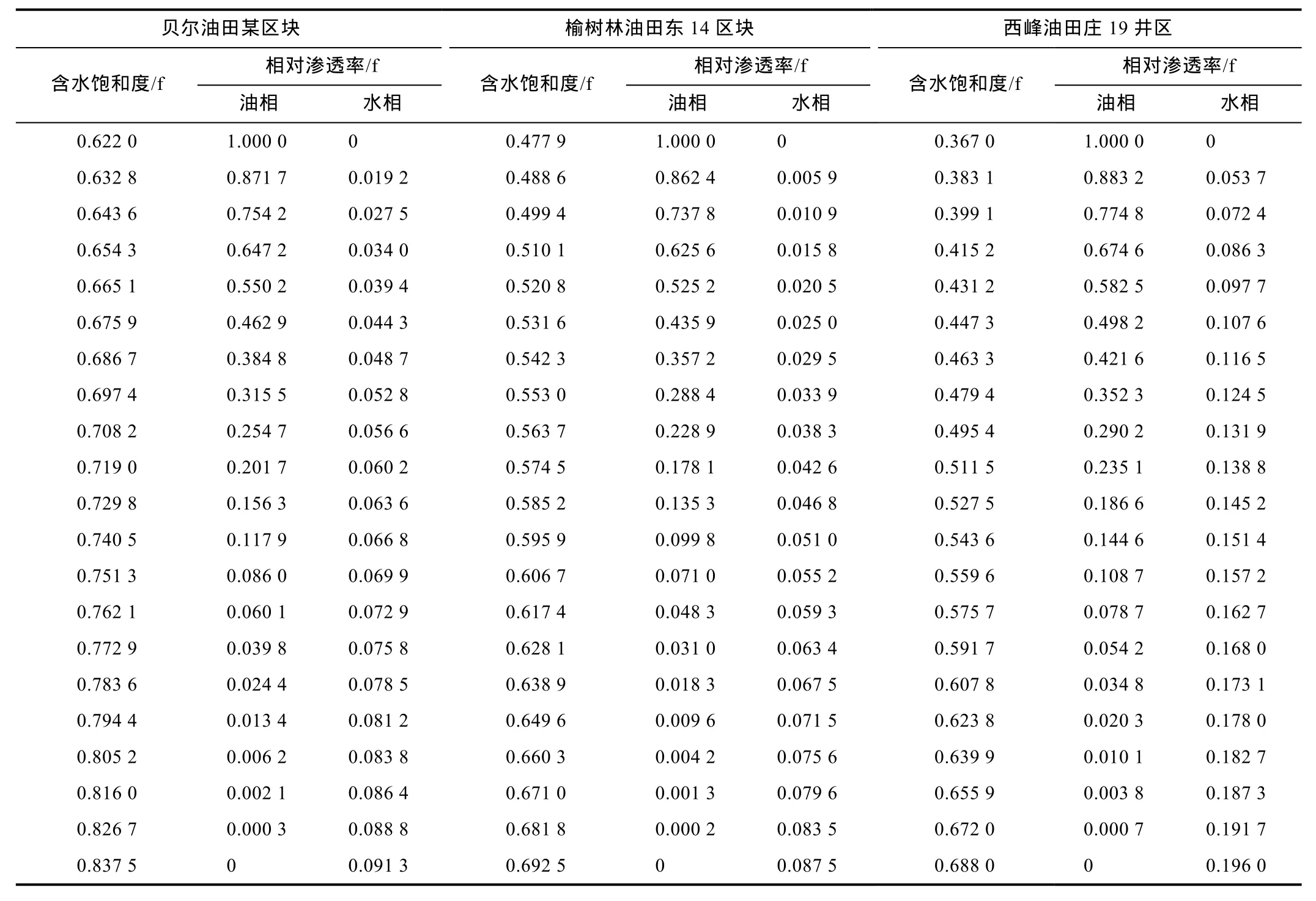
表2 不同区块岩心相对渗透率数据

图2 不同区块岩心Kro/Krw随Sw变化曲线
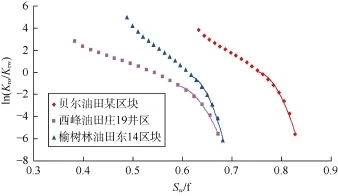
图3 Kro/Krw-Sw曲线偏移段拟合图

表3 Kro/Krw-Sw曲线偏移段拟合结果
3 新型水驱特征曲线关系式理论推导
根据以上对高含水阶段Kro/Krw与Sw关系曲线的描述和二者关系式的拟合,推导了高含水期油田水驱特征曲线关系式。
由岩心相对渗透率数据拟合得出油水两相流动出口端 Kroe/Krwe与出口端 Swe在高含水阶段满足以下关系:
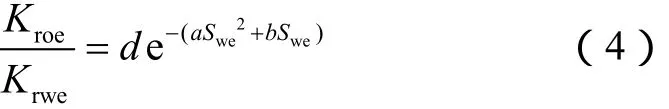
若不考虑重力和毛管力的影响,在水驱稳定渗流条件下,油水两相流动出口端 Kroe/Krwe与油、水瞬时产量存在如下关系[12]:
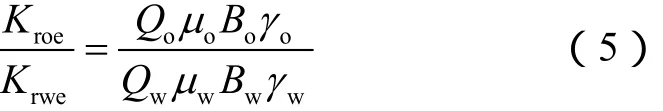
由(4)式和(5)式可得出水油比WOR的表达式为:

文献[1]应用 Buckley-Leverett前沿推进方程[13]、Welge平均含水饱和度方程[14]和艾福罗斯实验理论研究成果,推导得到出口端含水饱和度和采出程度的关系:

对(6)式取常用对数,并将(7)式代入可得:

即可得出高含水期油田水驱特征曲线关系式:

由R = Np/ N可得高含水期油田水油比与累计产油量关系式为:
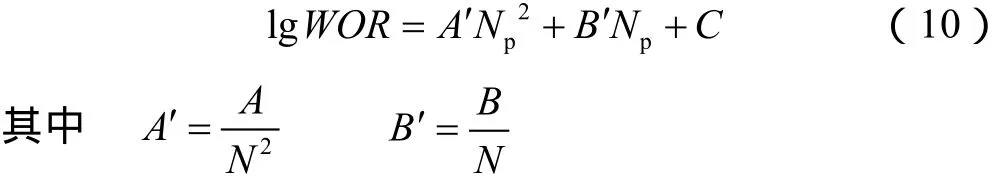
当油田开发达到废弃条件的经济极限水油比WORmax时,由(10)式可得计算水驱可采储量的公式为:

4 实例验证
为验证高含水期油田新型水驱特征曲线的实用性和适用性,选取文献[15]和[16]中油藏实际数据进行应用计算与结果分析。
4.1 Craig F F Jr文献算例
文献[15]中某油藏油水相对渗透率和水相分流量(即含水率)随含水饱和度的变化关系与见水后油藏生产动态数据分别见表4和表5(前4列)。由文献[1]可知,水驱油藏采出程度解析计算公式为:

由此可以计算出文献[15]中油藏出口端不同含水饱和度对应的采出程度、累计产油量和累计产水量等生产数据。其中油藏原始含水饱和度为0.1;当油藏开始见水时,出口端含水饱和度为0.469,累计产水量为0。

表4 某油藏相对渗透率和水相分流量随含水饱和度变化表[15]
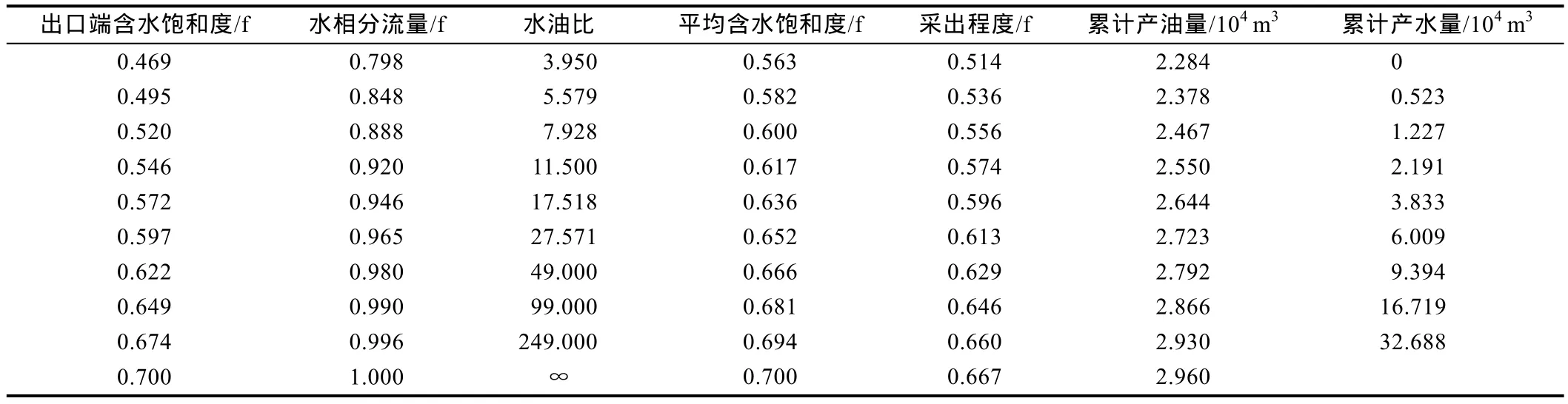
表5 见水后油藏生产动态数据
基于以上计算结果,本文绘制了lgWOR随累计产油量Np的变化关系曲线(见图4)。图中水驱特征曲线前半段符合传统的直线关系,而后半段出现明显上翘现象。分别利用乙型水驱特征曲线关系式和高含水期油田水驱特征曲线关系式对该曲线前、后两段进行拟合,并利用常用的甲型、乙型、丙型、丁型、张金庆型和陈元千两段直线式水驱特征曲线方法对该油藏水驱极限可采储量进行预测(见表6)。
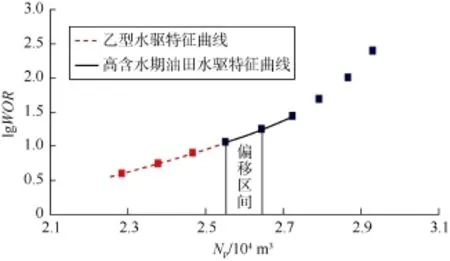
图4 文献[15]中油藏水油比随累计产油量变化曲线

表6 不同水驱特征曲线方法预测水驱可采储量结果
由图 4可见,乙型水驱特征曲线拟合前期曲线效果较好,后期曲线明显出现上翘现象,因此拟合效果较差。高含水期油田水驱特征曲线形态为抛物线,因此应用新水驱特征曲线拟合后期上翘点效果较好。在本算例中,由于利用(12)式计算生产数据,应用水驱特征曲线方法进行数据点拟合和可采储量预测,因此选用(12)式计算的含水率为0.98时的累计产油量(2.792×104m3)作为水驱可采储量标准值,进行水驱特征曲线方法预测结果对比分析。由表 6可见,利用高含水期油田水驱特征曲线预测的水驱极限可采储量与(12)式计算的结果吻合程度较好,表明针对高含水期油田,新方法相对而言具有较强的适用性。
为对水驱特征曲线在开发后期上翘的原因进行理论分析,本文绘制了该算例中岩心Kro/Krw随Sw变化曲线(见图 5),并与水驱特征曲线上翘现象(见图 4)进行对比分析。

图5 文献[15]中Kro/Krw随Sw变化曲线
由于原文献提供的均为散点值,因此无法准确确定图4和图5中直线段偏离点,但可以确定,图4中水驱特征曲线偏移直线段的转折点所处区间累计产油量为(2.550~2.644)×104m3(对应含水率为0.920~0.946),与图5中曲线偏离直线段的转折点所处含水饱和度区间0.55~0.60(对应含水率为0.925 0~0.966 5)基本吻合。由此可以说明,常见的油田开发后期水驱特征曲线上翘现象主要是由高含水阶段 Kro/Krw-Sw关系偏离半对数直线关系导致的,该分析结果同时证明了新型水驱特征曲线关系式推导基础的合理性。
4.2 濮城油田沙一段油藏实例
濮城油田沙一段油藏实际地下生产数据见文献[16]。已知沙一段油藏原油体积系数为1.429 9 m3/m3,地层水体积系数为1 m3/m3,可以计算出沙一段油藏地面累计产油量、地面累计产水量、地面累计产液量和含水率等生产数据(见表 7),其中地下与地面累计产水量数值相等。
基于以上计算结果,绘制了濮城油田沙一段油藏lgWOR随Np的变化关系曲线(见图6),其中1984年含水率仅为0.180 4,水驱特征曲线尚未表现出直线段特征,因此本研究中未考虑该数据。
由图 6可以看出,曲线前半段符合传统的直线关系,而在开发后期出现明显上翘现象。利用高含水期油田水驱特征曲线关系式对曲线后半段进行拟合,得到水油比与累计产油量的关系式:
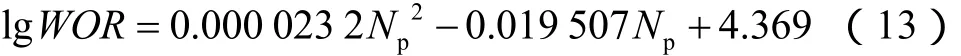
将相关系数带入(11)式计算得到濮城油田沙一段油藏水驱可采储量为667.95×104m3。
水驱开发效果评价方法较多[17-20],产量递减法是应用最普遍的方法之一。为验证新方法的计算结果,利用广义递减类型中的扩展Arps方法计算该油藏可采储量,进行对比分析。扩展Arps递减方法由陈元千教授于1994年提出,该方法将指数递减和调和递减看作双曲线递减的两种特定递减类型,进而以双曲线递减为基础推导出的可用于预测可采储量的广义递减类型方法[21-22]。

表7 濮城油田沙一段油藏实际开发数据表

图6 濮城油田沙一段油藏水油比随累计产油量变化曲线
由濮城油田沙一段油藏开发动态曲线可以看出(见图7),该油藏于1986年进入递减阶段。为了准确预测油藏可采储量,选取1988年作为预测递减阶段最大累计产量的起始点。濮城油田沙一段油藏递减阶段选取段生产数据见表8。
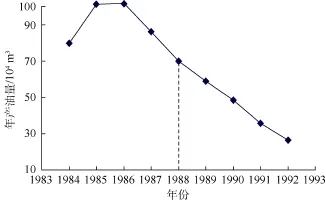
图7 濮城油田沙一段油藏开发动态曲线
根据线性回归试差法求解,取递减指数等于 0可以得到一条拟合相关系数为 0.999的直线(见图 8),表明该油藏递减阶段年产油量按照指数递减规律变化。通过拟合得出自1988年开始递减阶段累计产油量与年产油量的关系式为:

表8 濮城油田沙一段油藏递减阶段选取段产量数据表

图8 扩展Arps方法线性试差结果图

由文献[22]查表得出递减率时间换算系数为 1.0,从而得出递减阶段的最大累计产油量为 141.88×104m3。已知递减阶段选取段前累计产油量为530.32×104m3,故濮城油田沙一段油藏可采储量为 672.2×104m3。
通过对比分析,利用高含水期油田水驱特征曲线关系式计算的濮城油田沙一段油藏可采储量(667.95×104m3)与广义递减类型扩展 Arps方法计算结果(672.2×104m3)吻合程度较好,从而验证了新方法的实用性。
但是,针对递减指数等于 0、0.5或 1.0的常用递减类型之外的产量递减规律,扩展 Arps递减法需要利用电脑程序,在0~1的区间,以一定的步长(如0.01)给定不同的递减指数数值,进行线性试差,从而确定相关系数和拟合直线效果最佳的递减指数[22],计算过程较为复杂。高含水期油田水驱特征曲线方法避免了线性试差法确定递减指数的复杂过程,同时较好地解决了水驱特征曲线后期上翘导致的可采储量预测难题。
5 结论
传统水驱特征曲线推导的理论基础是中含水阶段Kro/Krw与Sw在半对数坐标中成直线关系,因此较适用于中含水期油田开发指标预测,若将该方法应用于高含水期油田,预测可采储量结果存在一定误差,以至于影响了传统方法的应用。
高含水阶段Kro/Krw与Sw在半对数坐标中偏离直线关系,是水驱特征曲线在开发后期经常出现上翘现象的主要原因。
高含水期油田水驱特征曲线表达式为二项式,曲线形态为抛物线,而甲、乙型水驱特征曲线形态为直线,因此新方法能够较好地拟合油田开发后期水驱特征曲线的上翘数据点。
当油田开发后期水驱特征曲线出现上翘特征时,建议选用新型水驱特征曲线关系式进行开发动态预测,可以较好地解决因水驱特征曲线上翘导致的可采储量预测难题。实例计算结果表明新方法具有较好的实用性。
符号注释:
Kro,Krw——油、水的相对渗透率,f;Sw——含水饱和度,f;Wp——累计产水量,104m3;Np——累计产油量,104m3;Npmax——水驱可采储量,104m3;fwmax——经济极限含水率,f;WOR——水油比,f;WORmax——经济极限水油比,f;Lp——累计产液量,104m3;a1,a2,a3,a4,a5,b1,b2,b3,b4,b5,A1,A2,B1,B2,a,b,d,f,g,h,m,n,A,B,A′,B′,C,E——系数;Kroe,Krwe——油水两相流动出口端油、水的相对渗透率,f;Swe——油水两相流动出口端含水饱和度,f;Qo,Qw——油水两相流动出口端油、水的产量,m3/d;μo,μw——地层原油、地层水的黏度,mPa·s;Bo,Bw——地层原油、地层水的体积系数,m3/m3;γo,γw——地层原油、地层水的相对密度,f;N——原油地质储量,104m3;Soi——原始含油饱和度,f;Swi——原始含水饱和度,f;Sor——残余油饱和度,f;R——采出程度,f;Swa——平均含水饱和度,f;t——时间,a;Q——递减t时间的产油量,104m3/a。
[1] 陈元千. 水驱曲线关系式的推导[J]. 石油学报, 1985, 6(2): 69-78.Chen Yuanqian. Derivation of relationship of water drive curves[J].Acta Petrolei Sinica, 1985, 6(2): 69-78.
[2] 俞启泰. 几种重要水驱特征曲线的油水渗流特征[J]. 石油学报,1999, 20(1): 56-60.Yu Qitai. Characteristic of oil-water seepage flow for several important water drive curves[J]. Acta Petrolei Sinica, 1990, 20(1):56-60.
[3] 俞启泰. 张金庆水驱特征曲线的应用及其油水渗流特征[J]. 新疆石油地质, 1998, 19(6): 507-511.Yu Qitai. Application of Zhang’s water drive curve and its characteristics of oil-water seepage flow[J]. Xinjiang Petroleum Geology, 1998, 19(6): 507-511.
[4] 陈元千, 陶自强. 高含水期水驱曲线的推导及上翘问题的分析[J].断块油气田, 1997, 4(3): 19-24.Chen Yuanqian, Tao Ziqiang. Derivation of water drive curve at high water-cut stage and its analysis of upwarding problem[J].Fault-Block Oil & Gas Field, 1997, 4(3): 19-24.
[5] 陈元千. 油田可采储量计算方法[J]. 新疆石油地质, 2000, 21(2):130-137.Chen Yuanqian. Calculation methods of recoverable reserves of oilfields[J]. Xinjiang Petroleum Geology, 2000, 21(2): 130-137.
[6] 陈元千. 水驱曲线法的分类、对比与评价[J]. 新疆石油地质, 1994,15(4): 348-356.Chen Yuanqian. Classification, correlation and evaluation of water-drive performance curve analysis method[J]. Xinjiang Petroleum Geology, 1994, 15(4): 348-356.
[7] Craft B, Hawkins M F. Applied petroleum reservoirs engineering[M].New Jersey: Prentice-Hall Inc., 1991: 340-341.
[8] 于波, 孙新敏, 杨勇, 等. 高含水期水驱特征曲线上翘时机的影响因素研究[J]. 石油天然气学报, 2008, 30(2): 127-131.Yu Bo, Sun Xinmin, Yang Yong, et al. Influential factor of upwarping moment of water-flooding characteristic curve at high water-cut stage[J]. Journal of Oil and Gas Technology, 2008, 30(2): 127-131.
[9] 高丽, 宋考平, 马春华, 等. 二段直线法预测高含水期油田开发指标[J]. 石油钻探技术, 2008, 36(5): 72-74.Gao Li, Song Kaoping, Ma Chunhua, et al. Two straight lines to forecast development index of high water-cut oilfield[J]. Petroleum Drilling Techniques, 2008, 36(5): 72-74.
[10] 陈元千. 平均相对渗透率曲线的标准化方法[J]. 石油工业标准与计量, 1990, 6(3): 6-9.Chen Yuanqian. Standardized method of average relative permeability curve[J]. Oil Industry Standard and Measurement, 1990,6(3): 6-9.
[11] 董大鹏. 低渗透油田油水两相渗流机理研究[D]. 成都: 成都理工大学, 2007: 60-62.Dong Dapeng. A study of percolation rules of oil-water two-phase flow in low-permeability reservoirs[D]. Chengdu: Chengdu University of Technology, 2007: 60-62.
[12] 姜汉桥, 姚军, 姜瑞忠. 油藏工程原理与方法[M]. 东营: 中国石油大学出版社, 2006: 239-241.Jiang Hanqiao, Yao Jun, Jiang Ruizhong. The fundamental and practice of reservoir engineering[M]. Dongying: China University of Petroleum Press, 2006: 239-241.
[13] Buckley S E, Leverett M C. Mechanism of fluid displacement in sands[J]. Trans AIME, 1942, 146(1): 107-116.
[14] Welge H J. A simplified method for computing oil recovery by gas or water drive[J]. JPT, 1952, 4(4): 91-98.
[15] Craig F F Jr. The reservoir engineering aspects of waterflooding[M].New York: Society of Petroleum Engineers of AIME, 1971: 112-114.
[16] 高文君, 徐冰涛, 王谦, 等. 利用水驱特征曲线确定活塞式驱程度指数的方法[J]. 新疆石油地质, 2000, 21(4): 311-314.Gao Wenjun, Xu Bingtao, Wang Qian, et al. Using water drive curves for determination of piston displacement degree index[J]. Xinjiang Petroleum Geology, 2000, 21(4): 311-314.
[17] 纪淑红, 田昌炳, 石成方, 等. 高含水阶段重新认识水驱油效率[J]. 石油勘探与开发, 2011, 38(3): 338-345.Ji Shuhong, Tian Changbing, Shi Chengfang, et al. New understanding on water-oil displacement eficiency in a high water-cut stage[J]. Petroleum Exploration and Development, 2011,38(3): 338-345.
[18] 李巧云, 张吉群, 邓宝荣, 等. 高含水油田层系重组方案的灰色决策优选法[J]. 石油勘探与开发, 2011, 38(4): 463-468.Li Qiaoyun, Zhang Jiqun, Deng Baorong, et al. Grey decision-making theory in the optimization of strata series recombination programs of high water-cut oilfields[J]. Petroleum Exploration and Development, 2011, 38(4): 463-468.
[19] 邹存友, 常毓文, 王国辉, 等. 水驱开发油田合理油水井数比的计算[J]. 石油勘探与开发, 2011, 38(2): 211-215.Zou Cunyou, Chang Yuwen, Wang Guohui, et al. Calculation on a reasonable production-injection well ratio in waterflooding oilfields[J]. Petroleum Exploration and Development, 2011, 38(2):211-215.
[20] 许长福, 刘红现, 钱根宝, 等. 克拉玛依砾岩储集层微观水驱油机理[J]. 石油勘探与开发, 2011, 38(6): 725-732.Xu Changfu, Liu Hongxian, Qian Genbao, et al. Microcosmic mechanisms of water-oil displacement in conglomerate reservoirs in Karamay Oilfield, NW China[J]. Petroleum Exploration and Development, 2011, 38(6): 725-732.
[21] 陈元千. 双曲线递减的简化及确定可采储量的截距法[J]. 天然气工业, 1994, 14(4): 32-37.Chen Yuanqian. Simplification of hyperbolic decline and the intercept method of determining recoverable reserves[J]. Natural Gas Industry, 1994, 14(4): 32-37.
[22] 陈元千, 璗李. 现代油藏工程[M]. 北京: 石油工业出版社, 2004:137-146.Chen Yuanqian, Li Dang. Modern petroleum reservoir engineering[M]. Beijing: Petroleum Industry Press, 2004: 137-146.

