大矢跨比车行索道桥结构的可行性

景天虎，莫时旭，刘丽荣，邓康成(桂林理工大学广西岩土力学与工程重点实验室，广西桂林541004)

现代车行索道桥属于简易柔性悬索桥的桥梁大类［1－3］.这种桥梁主索的矢跨比必须小于1/35，以满足跨端行车的要求.因此桥梁主索的恒载拉力占总设计拉力的比重往往很大，致使索材的利用效率较低.为了降低主索的拉力，有学者建议加大桥梁主索的矢跨比，使之大于1/35;同时，缩短桥跨两端八字形横梁的吊臂高度，凭借稳定索把桥面索吊起，达到改善桥头纵坡的目的［4］.在此，把主索矢跨比大于1/35的索道桥称为大矢跨比索道桥，至今尚未见其研究文献.

本研究以黄河白浪车行索道桥(简称旧桥)为原型，拟定了一座主跨438 m的大矢跨比车行索道桥(简称新桥).新桥结构构件的空间力学特征显著，对其内力分析不能采用近似解析法［4－5］.因此，采用考虑主索和横梁大变形力学行为的几何非线性有限元法，借助于ANSYS软件来分析新桥结构的静力性能，并简要分析了该结构的经济性与施工可行性.

1 材料与方法

1.1 新桥恒载状态线形确定的起始位形

要采用有限元法确定恒载作用下主索成桥状态线形，首先必须确定结构建模的起始位形.再以该起始位形的几何参数为依据建立结构的有限元模型.以预期的主索成桥状态线形为目标，通过迭代分析来逼近，进而最终确定各构件恒载平衡状态的几何参数，即进行一般悬索结构的找形分析［6－7］.在起始位形中设定主索曲线为互相平行的抛物线，其跨中矢高为9.131 m(图1a).但桥面索和内稳定索的线形在跨端局部区段略有变化，即在21#(21'#)横梁至支座之间的索形为水平直线，21#(21'#)横梁至19#(19'#)横梁之间的索形为倾斜线;同时它们互相平行，但不平行于外稳定索.其余区段的主索全部为互相平行的抛物线.

图1 成桥状态起始位形和桥梁横断面示意图Fig.1 Schematic graphs of initial geometrical configurations of the finished bridge under dead loads and its cross-section

1.2 新桥构件截面的拟定

初步拟定的新桥主索参数及横桥向布置与旧桥的相同，详见表1.从表1可见，每根钢丝绳的容许拉力为392.4 kN，钢丝总面积 5.8913 cm2，弹性模量为1.08 ×105MPa;木质桥面板的容许应力为17.64 MPa，弹性模量为8.83×103MPa;横梁的中部为工字形截面，吊臂为箱形变截面，弹性模量为2.06×105MPa，容许应力为333.2 MPa.本研究中所使用的旧桥结构数据见文献［4］，而实际设计桥梁时应按照最新的技术标准.

表1 旧桥上部结构参数Table 1 Structural parameters of old bridge superstructure

新桥的横梁全部采用由902钢板焊接而成的箱形截面，其布置数量和间距也与旧桥的完全相同.一般区段的横梁吊臂高度h=1.62 m(图1b)，21#(21'#)和20#(20'#)横梁吊臂高度分别为0.4358h(=0.706 m)和0.7030h(=1.139 m).经大量计算发现，不等长吊臂构造致使新桥的部分横梁受力情况极为不佳.因此，把新桥的横梁截面分为普通型和加强型两类，截面几何尺寸如图2所示.为了满足腹板的局部稳定要求，普通型横梁截面在受压区设置纵、横向加劲肋.设定桥面板与桥面索的约束作用可保证普通型横梁的整体稳定性.全桥共设39道普通型横梁，计入加劲肋后每道的质量为1.1 t.为了满足截面强度要求，加强型横梁的壁厚拟定得较大，不需设置加劲肋就能保证截面的局部稳定与整体稳定的要求;全桥共设4道加强型横梁，每道质量约为4.31 t.除21#、21'#、19#、19'#横梁采用加强型截面外，其余横梁都采用普通型截面.新桥横梁的总质量比旧桥的大11.54 t.

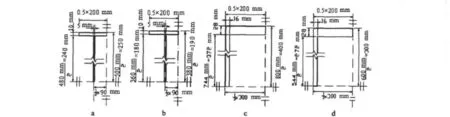
图2 横梁截面Fig.2 Cross-section of floor-beams

为了使新桥结构参数与旧桥的具有可比性，新桥的桥面板采用木板，其结构参数与旧桥的相同(表1).桥面恒载为0.254 kN·m－1(不含钢索和横梁质量).

由此可见，新、旧桥的绝大部分结构参数是相同的.

1.3 新桥的静力特性分析

对传统索道桥的静力特性分析可采用平面解析法，可取得较为精确的结果.而新桥的外稳定索与桥面索不平行，主索线形也由一整段单曲线变为多段复曲线.显然，新桥结构已经超出了平面解析法的适用范围［4］.要较为准确地把握它的结构特性，就必须采用有限元法从空间结构的角度来分析它.考虑到有限元建模和找形分析的收敛性对结构模型的要求，设定桥面系的连接构造能够保证在横梁与稳定索、桥面索之间的交点处无构件的相对滑动，因此，只建立中跨桥面索与稳定索的模型便能够较好地模拟整桥状态［7］.

1.3.1 有限元分析模型的建立 新桥整个结构是完全对称的.如图3所示，把起始位形中连接2组外稳定索曲线的跨中点所形成的直线段的中点，作为结构整体坐标系的原点，以X轴沿桥梁的纵向中轴线向右为正，以Y轴竖直向上为正，以Z轴为横桥向，正方向由坐标系的右手法则确定.结构分析采用大型通用有限元软件ANSYS.对于钢横梁中部水平段的箱形截面梁段采用空间梁单元beam 4模拟，共划分989个单元;对于箱形变截面的横梁吊臂采用空间梁单元beam 44模拟，共划分86个单元，如图3b所示.因钢箱梁属闭口薄壁杆件，大多数单元的长度比其横截面尺寸短，故在钢横梁的梁单元实常数输入时应考虑剪切变形影响项.设定横梁上密布的桥面索和桥面板与梁受压翼缘牢固相连，并能阻止受压翼缘发生侧向变位和扭转，故不考虑钢箱梁单元的翘曲自由度［8］.稳定索和桥面索采用索单元link 10模拟，单元最大长度为1.607 m，共划分6292个单元.桥面板不承受纵向拉力，但能横向联系、约束桥面索，且可传递局部车轮荷载，其力学行为用横桥向的空间梁单元beam 4模拟，共划分989个单元.整个结构有限元模型的单元节点有7346个.因横梁中部水平段截面的形心与桥面板、桥面索截面形心间的竖向距离超过了0.25 m(即横梁截面高度的一半)，三者交叉点处的节点组采用耦合约束，共2580个.同时设定横梁和桥面板在桥面索、稳定索的约束下不能绕自身中轴线转动.主索支座采用固定铰支约束.

图3 全桥计算模型及其局部放大图Fig.3 Calculation model of the whole bridge and its partial enlarged graph

以每根主索拉力157.66 kN(旧桥在成桥状态恒载作用下的水平索力为268.3 kN)所对应的索应变值(2.48×10－3)为每个索单元的初应变，求出成桥恒载作用下新桥的平衡状态.该初应变值是经大量计算得到的.

1.3.2 成桥状态恒载作用下的找形分析 在ANSYS的求解代码模块部分，打开几何非线性开关，激活应力刚化效应，荷载子步数设置为20，结构自重为Y轴方向的惯性荷载.

1.4 运营活载作用下的受力分析

1.4.1 新桥的检算荷载标准 对新桥结构进行分析时荷载标准和荷载组合的选取参考文献［4］.为了使新、旧桥结构具有可比性，对新桥结构分析时采用文献［4］中对旧桥分析所采用的荷载标准和荷载组合，即一种基本可变荷载(对应索道桥检算的坦克车或汽车荷载)与一种永久荷载(对应索道桥检算的恒载)相组合.

据此，新桥检算所采用的活载标准为:(1)3辆履带式坦克总重1177.2 kN;(2)9辆车轮式卡车总重882.9 kN.上述恒活载及其布载图式采用旧桥的数据.旧桥的构件内力检算采用容许应力法(安全系数为2.5)，计算时也不考虑4根外伸八字形简易抗风索的作用.为了使分析具有可比性，对新桥的结构分析亦如此处理.1.4.2 新桥的活载布置图式 新桥的活载加载图式采用如下6种荷载工况［4］.工况A:沿桥梁纵横向中心轴线对称布置1177.2 kN坦克荷载，纵桥向车距150 m(图4a);工况B沿桥梁纵、横向中心轴线对称加载882.9 kN卡车荷载，纵桥向车距50 m(图4b).工况C:在工况A的基础上，把跨中坦克车横桥向偏置0.3 m加载.工况D:在工况B的基础上，将跨中卡车横向偏置0.6 m加载.工况E:1177.2 kN坦克荷载在横向中心布置，但在纵向将第1辆坦克车布置于跨端横梁处(图4c).工况F:882.9 kN卡车荷载横向仍中心布置，但在纵向将第1辆卡车布置于跨端横梁处(图4d).工况A和B的目的是检算在预期的活载布置下钢索及钢横梁的强度是否满足要求;工况C和D的目的是检算在最不利的活载布置下索道桥抗横倾的能力，即检查桥面横向倾斜角是否超限(最大限值为3°);工况E和F的目的是检算在最不利的活载布置下桥梁跨端纵坡是否满足限坡要求(履带式坦克和轮式车辆的最大限坡分别为13%和10%).

图4 荷载纵向加载示意图Fig.4 Schematic diagrams of load cases acting longitudinally

每辆车荷载是按履带或车轮实际的空间分布尺寸施加到相应的桥面单元上的，故图4只表示每个车辆荷载合力的作用位置.

2 结果与分析

2.1 成桥状态恒载作用下的找形分析

采用upgeom命令将求得的节点位移值叠加到找形起始有限元模型的各节点上，更新模型后便得到成桥状态恒载作用下桥梁平衡状态的几何形状，此时，纵向桥面索为一条平顺的曲线.19#(19'#)横梁至右(左)跨端区间的桥面索也由起始位形的折线变为平滑曲线;在横桥向，每道桥面板和横梁的水平段的各相邻节点的竖向相对变位小于1 mm.由文献［4］可知，找形分析得到的桥面索线形满足索道桥桥面的行车要求.

从表2可见，主索设置的初应力(索单元的初应变)使得新桥在成桥状态恒载作用下跨中矢跨比大于旧桥.根据起始构形，在寻求恒载平衡态过程中结构以竖向变位为主.这是因为结构几何形状在水平面关于X和Z轴对称，而重力荷载只作用在竖向面内.

表2 恒载工况作用下主索跨中最大位移1)Table 2 Maximum displacements at mid-span of main cables under dead load

由理想柔性索几何线形的悬链线解析公式［4］可知，在成桥状态恒载基本不变的情况下，主索跨径所对应的等代简支梁跨中弯矩也不变，这时主索的水平索力决定其跨中矢高［1］;而不同的主索水平索力又对应于索单元不同的初应力值.因此，不同横梁位置所对应的等代简支梁的跨中弯矩相近，同时在找形分析时索单元所设置的初应力值也相同，那么最终得到的索道桥成桥平衡态的跨中矢跨比也会很接近.这为索结构找形分析时索单元初应变的合理选择提供了判据.

2.2 活载作用下的结构内力

上述6种荷载工况的部分计算结果列于表3－5.在表5中，横梁最不利截面位于其水平段端部与内稳定索形心轴交点处的截面.在荷载工况E作用下，横梁横截面的最大、最小应力值分别为329.87、－329.60 MPa，发生位置为21#(21'#)横梁水平段端部.

表3 荷载工况A作用下主索跨中的最大位移1)Table 3 Maximum displacements at mid-span of main cables under load in case A

表4 每种承重索的单根轴向拉力极值Table 4 Extremum of axial tensile force of single piece of each kind of main cables

表5 横梁受力最不利截面的内力1)Table 5 Internal forces on the most unfavorable cross-section of floor-beams kN·m－1

因为索道桥结构具有很强的几何非线性特性，不能象常规桥梁结构那样先分别求出恒载、活载的效应值，然后利用线性叠加原理求出二者的组合值(即总效应值).本文所有计算结果都为恒、活载作用下的组合值(即总效应值).从表3可知，在荷载工况A作用下新桥的矢跨比大于1/35(常规车行索道桥矢跨比的上限值)，可见，新桥是大矢跨比索道桥.从表4－5可知，其主索的水平索力(240.85 kN)比旧桥的(300.21 kN)［4］下降了19.77%.这说明主索设置较大的跨中矢跨比可产生预期的结构效应.显然，主索找形时设置的初应变越小，成桥恒载状态及满布活载状态的跨中矢跨比就越大，主索内力下降的幅度也越大.在所有荷载工况下，主索索力的极值均小于单根钢索的容许拉力(392.4 kN).

由表4可知，虽然桥面系荷载是直接作用在桥面索上的，主索的最大索力出现在外稳定索上而不是在桥面索上，并且最大值出现在跨端横梁(X=±207.75 m)的位置.这说明缩短横梁的吊臂长度能把更多的桥面荷载传向稳定索.与一般单跨悬索的索力极值分别出现在索跨跨端与跨中的情况不同，新桥的内稳定索和桥面索的索力极值出现在跨端横梁处.由此可见，截面加强型横梁对主索索力的纵、横向分布都具有显著的调配功能.

从表5可知，在各根横梁受力最不利截面上的弯矩My反映了横梁对横桥向布置的各根主索拉力的调配作用，正是各根主索的拉力差形成My.另外，My值由跨中横梁向跨端横梁逐渐增大，但在19#横梁(位于纵桥向的吊臂等长与不等长横梁所在区段的交界位置)水平段端部的最不利截面上出现了剧增，之后在20#横梁上剧降，最后在21#横梁上剧增至最大值.横梁截面上的弯矩Mz反映了横梁对局部竖向荷载具有由桥面索向内、外稳定索的传递及再分配的功能.因此，在每种荷载工况下，位于车辆荷载附近的横梁横截面上的Mz均较大;同时，在跨端附近的19#和20#横梁上Mz出现了较大的量值(21#横梁达到了极大值).这也就是对该位置的横梁采用加强型截面的原因.

与弯矩内力相比，各荷载工况下单元轴向内力N小得多.这是因为从分析结果得到的受力最不利截面位于横梁的水平段，所考察的荷载又都是竖向作用的，不会对构件产生很大的水平拉力.

由表5可知，横梁最不利的加载情况出现在荷载工况E.在该工况作用下21#(21'#)横梁受力最不利截面的应力达到了极值，但其绝对值仍小于容许值(333.2 MPa).由此可见，横梁的强度满足要求.

由图5可知，在竖向平面内桥面板挠曲变形非常小，完全满足行车要求.

即使没有考虑抗风索的横向稳定作用，当桥上的3辆坦克车中有一辆在跨中偏载行驶时(即荷载工况 C)，桥面横倾角(1.3331°)不到限值(3°)的一半，也达不到旧桥在该工况下横倾角(2.817°)［4］的一半;9辆卡车中有一辆偏载(即荷载工况D)引起的桥面横倾角则更小(新桥的为0.8307°，旧桥的为2.945°).由此可见，横梁和稳定索对车行索道桥抵抗横向倾覆、保证行车安全的作用是很显著的.

一般单跨悬索曲线的跨端斜率(索道桥的桥面纵坡)随跨中矢高的增大而增大.为了满足索道桥的行车要求，履带车的桥梁跨端的纵坡［4］应小于13%;轮式车的应小于10%.在工况E下，新、旧桥的跨端纵坡分别为10.328%、10.6%;在工况F下，新、旧桥的跨端纵坡分别为9.217%、9.7%.由此可见，虽然新桥的矢跨比大于旧桥，但新桥跨端的桥面纵坡仍满足限坡要求，且略小于旧桥.当然，桥面纵坡越小对行车越有利.由此可见，缩短跨端横梁吊臂的竖向高度，能改善大矢跨比索道桥的桥头纵坡.但应看到，为了能省去常规公路悬索桥上所设置的高大桥塔，索道桥跨端稳定索与桥面索的支座所设置的高差不会很大(新桥为1.37 m)，跨端横梁吊臂缩短的幅度也不会很大.因此，采用这种方法改善跨端桥面纵坡的效果很有限，新桥在满布活载时矢跨比不大于1/32，达不到常规公路悬索桥主索矢跨比(1/10左右).

图5 工况A作用下桥面板局部区段的斜视图Fig.5 Oblique view of partial section of pavement slabs under load in cases A

2.3 新桥结构的施工可行性

新、旧桥构件的最大区别在于后者的横梁吊臂等高，而前者的则不等高.但吊臂不等高横梁的数量很少，且只设在跨端附近.黄绍金等［4］认为一般索道桥的各根主索是等长的.采用有限元方法分析的结果表明，新桥的稳定索和桥面索的索长并不相等.例如，在成桥恒载平衡态时外稳定索的有应力和无应力索长分别为438.507和437.011 m，而桥面中心索的有应力和无应力索长则为439.486和438.129 m.这主要是由于新桥结构的全桥横梁吊臂不等长，在找形分析时所设定的索形起始位形中稳定索与桥面索的线形不平行，二者的无应力索长也就不相等了.横梁的主要作用之一就是把桥梁横断面内分布不均匀的竖向荷载在稳定索与桥面索之间进行调配.受载后长达14 m的横梁沿横桥向的竖向挠度不完全相同，经过它的调配后稳定索和桥面索的内力也不相同，从而导致二者的有应力索长不相同.另外从表1可知，虽稳定索和桥面索的长度不同，但它们的跨中矢跨比却非常接近.这主要是由于二者的长度差(1 m左右)相对于438 m的主跨径而言很小.一般来说，各种承重索的矢跨比不同，它们所受的拉力也不会相同，从而影响各根主索受力的均衡性，这对索道桥的安全稳定性是不利的.但从前面分析可知，新桥结构抵抗横向倾覆的安全稳定性优于旧桥，这说明前者的加强横梁构造对桥梁横断面内的偏载作用具有更有效的横向分配功能.除此之外，新、旧桥的其他构件的构造是基本相同的.因此，把旧桥的施工方法［4］略加修改，即可用于新桥的建造.

2.3.1 横梁安装位置的标记 确定横梁安装位置时要使用记号符合法［9］.首先根据新桥在成桥恒载平衡状态时各根钢索的单元内力和应变反算出它们的无应力长度，以及横梁与主索的交点在无应力钢索长度方向上的投影位置;然后在钢索下料时在横梁的安装位置标上记号.在主索初挂的空索状态只要让每道横梁的位置与钢索上相应记号相符合，就可固定横梁，完成安装工作.

2.3.2 横梁的展放 如图6所示，施工时展放横梁不能采用一岸展放法，而应采用两岸向桥跨中的展放法.新桥的每个跨端附近有2根横梁的吊臂缩短了，展放这些短臂横梁时，它们在主索上的滑动受到很大阻力，安装时若从一岸展放，它们要滑过主索一个整跨长度才能到达对岸的安装位置.若采用两岸展放法，短臂横梁是最后安装的，它们从主索上滑过的距离很短，因而安装也就容易得多.总之，采用现有施工技术能较容易地建造大矢跨比索道桥，该结构形式的施工可行性好.

2.4 新桥结构的经济性分析

在没有对新桥进行主要构件优化的情况下，新、旧桥的桥面板材料用量基本相同，而新桥钢横梁的总质量比旧桥的大了11.54 t.根据主索找形分析的线形结果和结构内力分析的应变结果可以求出优化设计后新桥的钢索总质量为146.491 t，比旧桥节省了36.161 t.因此，实际设计大矢跨比索道桥时，最终设计结果应该是调整优化后的桥梁结构，而不是初步拟定的结构.显然，最终实施的新桥全桥荷载相对于旧桥减小了，进而主索对鞍座的竖直拉力也比旧桥的小.

据此初步估算，当抵消横梁总质量的增量后，新桥的上部结构比旧桥的轻了241.53 kN.这里还没有考虑到钢索自身截面变小，恒载减小.通过进一步减小钢索的截面面积，节省更多索材工程量.

最后，再考虑材料价格因素，钢索的材料单价约是横梁钢板材料的2倍，因此新桥相对旧桥具有显著的经济性优势.

图6 横梁安装示意图Fig.6 Schematic diagrams for erection of floor-beams

新桥结构实际上只是对原有索道桥结构的少量构件进行了升级改造，使得前者具有显著的经济性.因此，对旧桥结构的这种改良具有很高的工程效率.

3 结论

首先拟定了大矢跨比索道桥的结构方案，并分析了它的静力特性.最后通过对比，考察了其施工可行性与经济性，得出如下结论.

(1)大矢跨比索道桥力学行为的空间效应更加显著.用于传统索道桥结构分析的平面解析法不宜用于这种结构的内力分析.只有采用能考虑到结构构件空间效应的几何非线性有限元法对其做精细分析，才能正确把握其力学特性.

(2)缩短索道桥跨端附近横梁的吊臂长度能改善桥头纵坡，但改善幅度有限.因受跨端桥面纵坡的限制，索道桥的主索跨中矢跨比很难达到常规公路悬索桥的主索矢跨比.

(3)大矢跨比索道桥的结构行为参数达到常规索道桥的技术要求;其所有构件的安装完全可采用现有的常规施工技术来实现，具有可施工性;并且该结构的经济性优势显著.由此可知该结构形式是完全可行的.

［1］周新年.工程索道与柔性吊桥——理论 设计 案例［M］.北京:人民交通出版社，2008:245－247.

［2］周新年，郑丽凤，游明兴，等.柔性吊桥设计理论及其应用研究Ⅳ.简易柔性悬索桥总体设计方案研究—福建省建瓯市慈口悬索桥例析［J］.福建林学院学报，2001，21(3):203 －206.

［3］周新年，郑丽凤，冯建祥，等.柔性吊桥设计理论及其应用研究Ⅰ.福建省简易柔性悬索桥分析研究［J］.福建林业科技，2000，27(2):72 －74.

［4］黄绍金，刘伯生.现代索道桥［M］.北京:人民交通出版社，2004:243，154－180.

［5］王小桃，周新年，冯辉荣，等.基于VB 6.0的悬链线理论单跨索道侧型图设计［J］.福建农林大学学报:自然科学版，2012，41(2):149 －152.

［6］景天虎，李青宁.悬索桥主缆成桥线形确定的有限元新算法［J］.世界桥梁，2012，40(1):42－46.

［7］田仲初，卜铭，黄宏辉，等.临时索道桥的成桥状态确定与荷载试验研究［J］.长沙交通学院学报，2005，21(2):21－25.

［8］湖北省发展计划委员会.GB 50018-2002冷弯薄壁型钢结构技术规范［S］.北京:中国计划出版社，2002:22－24.

［9］白剑，赵小星，贺栓海.悬索桥主缆施工中的温度测试及温度影响的控制［C］∥中国公路学会桥梁和结构工程学会.2003年全国桥梁学术会议论文集.北京:人民交通出版社，2003:758－761.