葡萄酒质量评价的模型分析与优化

何 舒



葡萄酒质量评价的模型分析与优化

何 舒

(安徽财经大学 统计与应用数学学院，安徽 芜湖233000)

针对葡萄酒评价的问题做出了合理分析，通过偏最小二乘回归方法建立起葡萄酒与葡萄理化指标之间的关系，对葡萄理化指标的数据进行相关性分析和正太检验(非参数检验)，通过偏最小二乘回归方程呈现出葡萄与葡萄酒有关的因素对其质量的影响，基于此方程论证了：在实际生活中，不能简单根据酿酒葡萄与葡萄酒的理化指标评价葡萄酒的质量．并给出了其它影响葡萄酒质量的因素．

葡萄酒；理化指标；非参数检验；偏最小二乘回归法

葡萄酒的历史源远流长，但在中国经济还不景气的时候，葡萄酒得不到普及，随着人民生活质量的提高，葡萄酒带来的精神层面的作用越来越大，评酒文化也在悄然发展，出现了很多评酒人士，虽然评酒人士对葡萄酒文化与葡萄酒的专业知识充分了解，但是也避免不了个人品味的差异，这就需要制定评酒的标准，并确定评酒的各个层面．在长期的积累中发现，通过对外观、香气、口感与酒的总体评价这4个方面可以对葡萄酒进行比较全面的分析，不过再加上对每个评酒员的评分，利用数学模型进行分析会更加准确地评价各种葡萄酒的质量．

随着科技不断的进步，各种物质的理化指标也能够精确的测出，此时，葡萄酒的质量不仅仅是依据评酒员的感官进行评价，而且会与酿酒葡萄的理化指标、葡萄酒的理化指标都有一定的联系，如果能清晰地分析他们之间的关系将会对葡萄酒的酿造和葡萄酒的评价意义重大，本文就是鉴于以上的葡萄酒发展的现状对葡萄酒的评价问题进行深入研究的．

1 问题的分析

首先是通过网上查得2组评酒员的数据并对数据进行检验，利用非参数检验中的-检验验证2组数据之间有无显著性差异，而哪组的数据更加可信则是根据每组数据的方差大小判别，并利用这组比较可信的数据作为后面研究葡萄酒与葡萄理化性质之间的数据来源．

酿酒葡萄与葡萄酒的理化指标多而杂，因而它们之间的联系也是复杂的，评酒员在外观、香气、口感与平衡/整体评价葡萄酒进行打分，这4个评分角度的打分分别会受到葡萄酒的各种理化指标的影响，因而可以根据评酒员的打分对葡萄酒的质量进行评判．

而对于这种研究对象复杂繁多的问题，偏最小二乘回归法中的相关性分析可以解决，此方法专门针对具有多重性关系、联系复杂的数据分析，最后可以利用得到的相关性矩阵对两组数据中各指标一一对应地分析它们的联系．

在分析出葡萄与葡萄酒的理化指标之间的关系基础上，本文又研究了芳香物质对葡萄酒的质量有没有影响，即在自变量中加入芳香物质的各指标重新求解回归方程，通过前后两种方程之间的比较，得出芳香物质对葡萄酒质量的影响并进行论证．

2 合理的假设

1) 所查的葡萄酒与葡萄的理化指标能够充分反映葡萄与葡萄酒的性质．

2) 假设葡萄酒的理化指标与它的芳香物质没有重合部分，即这2组数据相互独立．

3) 假设在酿酒的过程中没有出现异常的化学或者物理反应，即数据都能反映正常情况下葡萄与葡萄酒之间的关系．

4) 评酒员对葡萄酒的评价都是客观公正的，并通过评酒员对葡萄酒的评价作为衡量葡萄酒的一个标准．

3 相关性分析

通过matlab编程求解得到酿酒葡萄与葡萄酒的理化指标之间的相关性矩阵，由于指标的种类比较多，相关性矩阵的数据庞大，只能截取红葡萄与红葡萄酒一部分数据进行代表性分析，部分矩阵见表1．

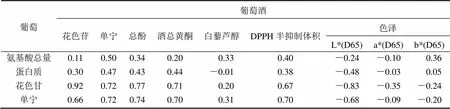
表1 红葡萄与红葡萄酒部分相关性矩阵的信息

从表1中可以看到数据有正有负，说明酿酒葡萄与葡萄酒之间的理化指标正相关与负相关的情况都有，表中每个数据的绝对值大小作为各指标之间相关程度大小分析的基础，绝对值越大说明这两个指标之间的联系越大，越小联系就越小．因此根据相关性矩阵中的所有数据就可以直观的看出葡萄与葡萄酒各理化指标之间的联系与联系程度．

4 判断葡萄酒的质量与芳香物质之间[3]的关系

1) 在酿酒葡萄与葡萄酒的理化指标中分别选择6个与2个作为自变量，这些变量分别用表示(具体的指标名称见符号说明)，葡萄酒的质量还是同样通过4个评分角度体现，即这4个评分角度的打分作为因变量，因变量用表示，建立到的回归方程，得到4个回归方程，回归方程的建立就能够确定这些自变量与因变量之间的联系．

2) 建立的方程中的系数就可以观察出每个自变量对因变量的影响程度，4个方程分别代表葡萄的质量4个方面，即酿酒葡萄与葡萄酒的理化指标对葡萄酒质量的影响问题得到解决．并可以通过多因变量的数据进行多种方式的改变会得到一系列不同的因变量的值，这也可以看出他们之间的联系与影响是复杂而多变的．

3) 在原有的8个自变量的基础上加上3个芳香物质的指标为：, 因变量依然不变，求解新的偏最小二乘的回归方程，最后通过对2种方程的系数与方程的差异大小论证，2种方程差别较大，则影响葡萄酒质量的不仅仅是2组理化指标，而是更多的数据．

根据模型建立的步骤求解没有加入芳香物质作为自变量求得系数，得到偏最小二乘的回归方程．

只含有红葡萄及红葡萄酒的指标：

.

.

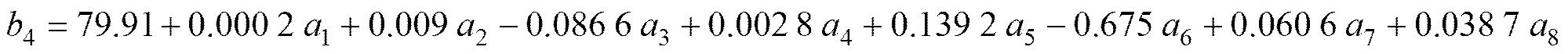
各指标对葡萄酒质量的影响有效益型也有成本型，根据方程中各指标的系数分析，从各方程中的系数大小可以看出各个指标对葡萄酒的影响差别比较大，并且每个方程的最前方都有一个常数，是因为为了反映原始数据的特征，以上的方程都是没有进行标准化处理的方程，能够更清楚的看出每个指标对数据的影响．

4) 加入芳香物质的3种指标作为自变量，求解得到红葡萄和红葡萄酒的回归方程为：

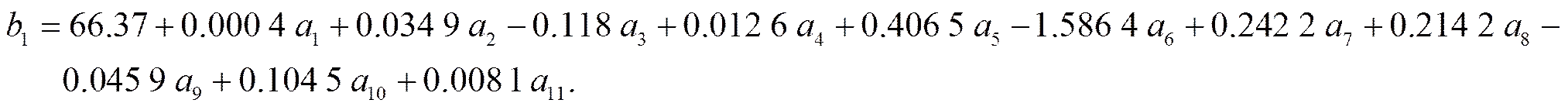
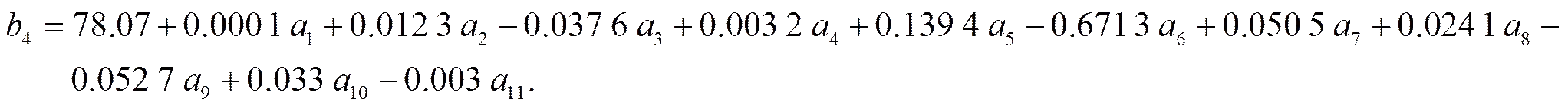
如图2回归系数的直方图能够更加直观地分析芳香物质对葡萄酒质量的影响，观察图形，不加入芳香物质时，总酚和柠檬酸(对应图1中柱形最高的两条)对两种葡萄的质量的影响较大，加入芳香物质后，总酚和柠檬酸对葡萄质量的影响仍然较大，芳香物质对两种葡萄质量的影响也相对较高．

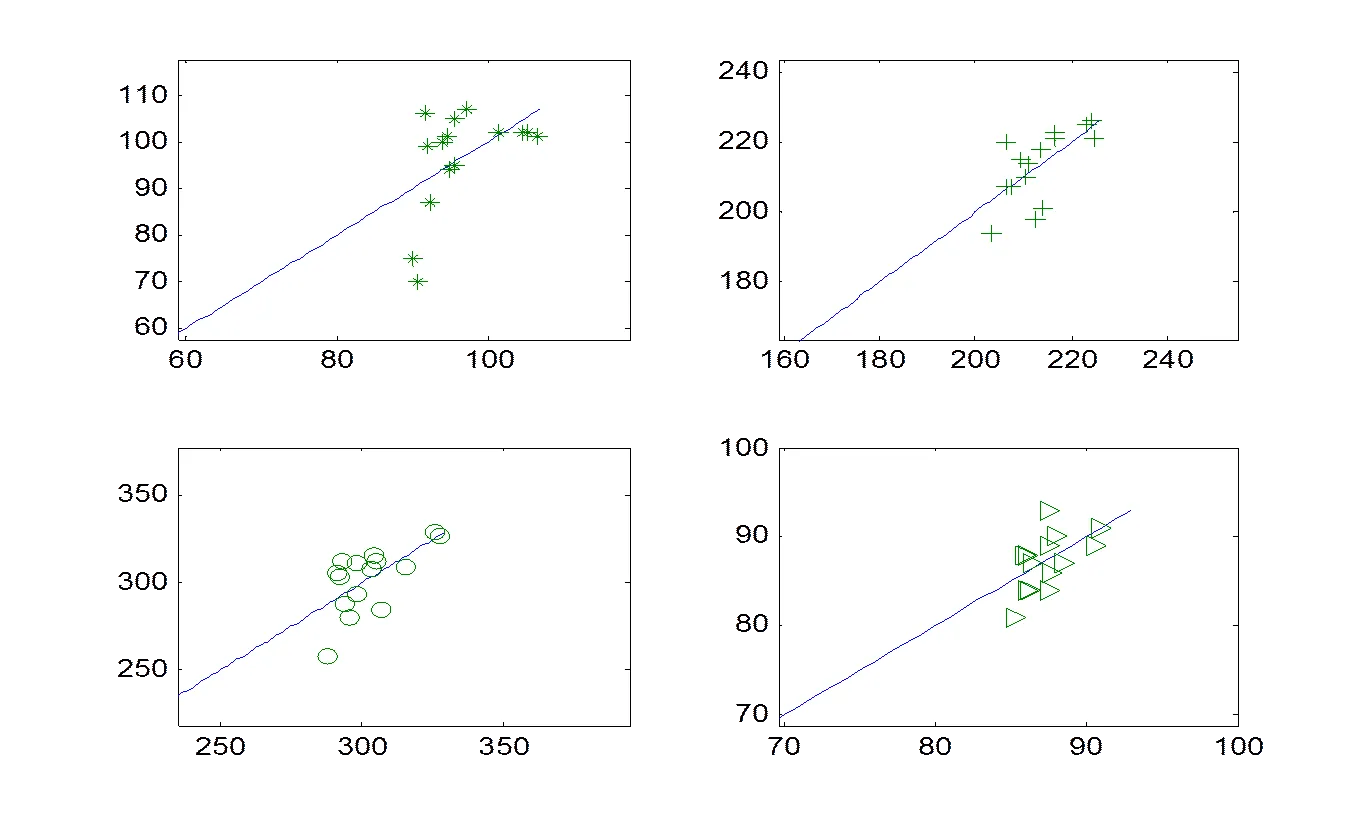
图2 葡萄酒质量预测图

那么，通过图与公式的结合分析，只用酿酒葡萄和葡萄酒的理化指标评价葡萄酒的质量不具有代表性与全面性，这两种指标只能说明原始材料对葡萄酒的影响，不能说明加工工艺及陈酿技术对葡萄酒质量的影响，也说明这一问题的论证结果是符合实际情况的．(注：分别表示外观分析、香气分析，口感分析与平衡/整体分析这4个方面的葡萄酒质量；方程中有的系数的绝对值大于1，是因为化学反应很复杂，系数绝对值大于1代表经过它的影响葡萄酒中可以有其它的物质转化为该中物质，即这种物质比初始的要多．)

5 偏最小二乘回归模型的检验

为了考察在使用偏最小二乘法得到的回归方程的模型精度，对回归方程绘制预测图，预测图是根据在matlab中改变自变量的数据，求得更多的数据，如果这些包含这些数据的点均匀地分布在参考线(检验点的线分布)的两旁，说明方程的拟合值与原值差异很小，拟合效果比较好，即回归方程具有较高的可信度，图2是以检验红葡萄没有加入芳香物质的回归方程为例．

4个回归方程的预测图都均匀分布在参考线的两侧，说明这4个回归方程的拟合效果很好，能够提供有用的数据．

6 结论

本文最主要是利用偏最小二乘回归模型对葡萄酒的评价问题进行分析．在平时的实践中，大多数的都是研究数据较多并且相关性比较复杂的问题，所以这种方法针对个数很多、存在多重相关性、观测数据的数量(样本量)又较少的数据分析有重要的作用，偏最小二乘法集中了传统的回归分析等方法的优点，是建模中数据处理不错的选择．并且得到的结论比较符合实际情况，即在实际生活中葡萄酒的质量与葡萄酒制作的原材料、酿造技术及其他的因素都有关系，不仅仅只是与葡萄或者葡萄酒的理化性质有关，具体的问题需要进一步的分析才能得出更加正确的结论．

[1] 岳俊波,杨冬松,贾旻.浅谈葡萄酒陈酿中游离氨基酸的含量对风味的影响[J].酿酒,2001,28(3):2-3.

[2] 王惠文,吴载斌,孟洁,等.偏最小二乘回归的线性与非线性方法[M].北京:国防工业出版社,2006:201-203.

[3] 于静,李景明,吴继红,等.葡萄酒芳香物质研究进展[J].中外葡萄与葡萄酒,2005,4(3):48-51.

[4] 刘闽碧.用excel做-检验与-检验[J].海峡预防医学杂志,2002,8(5):67-68.

Wine Quality Evaluation Model Analysis and Optimization

HE Shu

(College of Statistics and Applied Mathematics, Anhui University of Finance and Economy, Wuhu, Anhui 233000, China)

In this paper, we make a reasonable analysis on wine evaluation, establishing the relationship between the physical and chemical indicators of the wine and grape by the method of partial least squares regression, making correlation analysis and normal test (non-parametric tests) on the data of physicochemical index of grape. Through the partial least squares regression equation, it shows the related factors of grape and wine which affect its quality. The argument based on this equation: In real life, we can not simply evaluate wine quality based on physical and chemical indicators of wine grapes and wine. And we give some other factors that affect the quality of the wine.

wine; physicochemical index; non-parametric tests; partial least squares regression

(责任编校：李建明 英文校对：李玉玲)

O29

A

1673-2065(2013)04-0012-04

2013-03-09

何 舒(1992-),女,安徽芜湖人,安徽财经大学统计与应用数学学院本科生.