基于小波变换和支持向量机的电能质量扰动识别

陈华丰 乔 磊 柳双林

（西南交通大学电气工程学院，成都 610031）

随着工业的发展，大量非线性、冲击性和不平衡负荷在电力系统中投入使用，带来一系列电能质量扰动问题。电能质量扰动会导致设备过热、电机停转、保护失灵等后果，造成严重的经济损失和社会影响。对电能质量扰动的准确识别，能为电能质量的管理和治理提供辅助决策，可提高供电质量[1]。

电能质量扰动的识别过程一般包括特征提取和模式识别分类两个环节。特征提取是对原始信号进行变换提取出有效的分类特征，特征提取方法有时域、频域和时频域方法。时域分析方法主要分析以时域特征为主的信号，很难知道信号中含有的频率分量；同理频域方法不能给出信号某种频率分量随时间变化的情况。由于电能质量扰动信号绝大多数是非平稳信号，传统的FFT变换方法不能反映信号的时变特征，即信号频率随时间变化的情况，因此时频域分析方法[2]得到了广泛应用。常用的有短时傅里叶变换[1]、小波变换[3-6]、和 S-变换[7]。STFT是在非平稳信号分析中应用得最广泛的方法之一。但是其窗口固定，因此其时频分辨率固定，要改变其时频分辨率必须重新选择窗口。而小波变换克服了 STFT窗口固定的缺陷，具有变化的分辨率，在信号高频部分具有较好的时间分辨率，在低频部分具有较好的频率分辨率，因此小波变换具有良好的时频局部性能。本文采用小波变换提取扰动信号的特征，小波变换提取的特征输入到模式识别分类器中，就能实现扰动信号自动分类。常用的分类器有神经网络[4]、决策树[9]和支持向量机[3]等。神经网络方法训练时间长，容易陷入局部极值；决策树方法通过模拟人类的思维构建分类规则，但其规则建立起来比较复杂；SVM 是近年来提出的统计学习方法，在解决小样本、分线性以及高维模式识别问题中表现出良好的结果，本来选择SVM作为分类器。

以前文献采用小波变换提取能量分布特征时，一般做 10层或以上[3-6]的小波分解或者根据经验确定分解层数。本文根据扰动信号的采样率来确定小波分解的层数，只需做6层小波分解，减少了特征提取时间和特征维数，提取的特征输入到训练好的SVM 中就能实现扰动信号的自动分类；SVM训练过程中，其训练样本添加SNR在较大范围内分布比较均匀的噪声。测试结果表明，改进的方法提高了识别准确率。

1 小波变换提取特征向量

扰动信号小波变换多尺度分解的直接结果是各个尺度对应的一系列系数，这些系数是小波变换提取扰动信号特征的基础。利用小波变换提取的特征主要有：小波系数的平均值、方差、扰动持续时间及信号奇异点位置，依据 Parseval理论得到的各尺度能量或者其和正常信号的能量差值等。利用小波变换提取的特征通常很难根据“IF-THEN”的规则形式构建扰动信号分类系统。本文利用小波变换提取能量分布差特征，选用人工智能分类器—SVM进行分类。

1.1 小波变换原理

小波变换具有可变的窗口大小，可以信号频率的不同进行调整，具有良好的时频局部性能。小波变换的实质是利用小波函数及小波变换系数表达一个信号函数。设时域信号为 f(x)，其小波变换表达式可以表示为

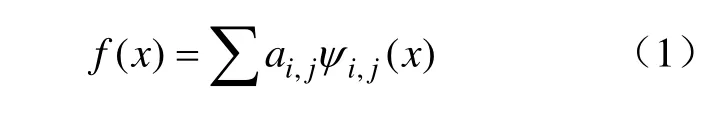
式中，i、j为整数，分别为伸缩因子、平移因子；ai,j为离散小波变换系数；ψi,j(x)为小波函数。离散小波变换系数可以通过式（2）得到：

小波函数ψi,j(x)可以通过小波母函数ψ(x)经过平移和伸缩变换得到：

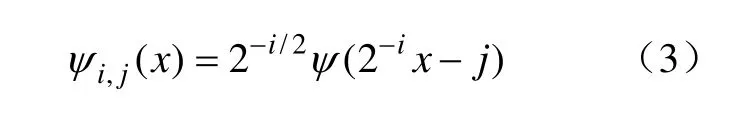
在进行多分辨分析的情况下，小波母函数必须满足下列方程：

利用小波变换分析扰动信号时，小波基的选择对信号处理起着关键作用。在对扰动信号分析处理时，目前还没有一个统一的小波函数对所有电能质量问题达到最佳效果。在众多的小波中，Daubechies（db）系列小波具有正交，时频紧支撑，高正则性和具有Mallat快速算法等特性[8-10]。db4小波具有最短的时窗和最高的时间分辨率，在非平稳信号检测中效果较好[11]。本文选择db4小波作为扰动特征提取的小波基。

1.2 能量分布特征提取

1）小波分解层次的确定

本文考虑6种扰动类型：电压暂升、电压暂降、电压闪变、谐波、电磁脉冲和振荡暂态，其数学模型方程来自于文献[12]，扰动信号的采用率为 fs为6400Hz，信号基频为 50Hz，即每个信号周波采样128点，总共采样10个电压周波。

已有文献在用小波能量分布做特征提取时，基本是做 10层或者以上的小波分解，并没有理论依据。本文根据信号采样率确定小波分解层数，使得基频位于最低子频带的中心，这样可以限制基频分量对其他子频带的影响。小波分解频带划分数目[13]为

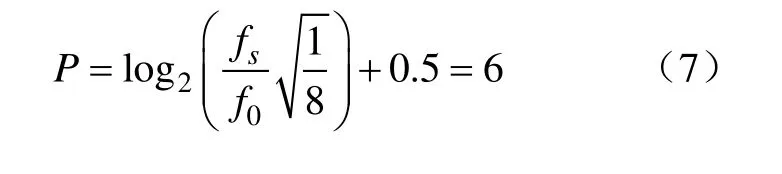
式中，fs为扰动信号采样率；f0为信号基频。这样只需对扰动信号进行6层小波分解。

2）能量分布差特征提取

根据Parseval定理，输入能量载入小波系数[2]，如下式：

式中，f(t)为待分解的信号，cj(k)为小波分解第 j层的近似系数，dj(k)为小波分解第j层的细节系数。

假如对获得的电能质量扰动信号进行 J层分解，小波变换的能量分布[3]定义为

式中，j=1, 2, …, J，这样经过 层小波分解，可以得到一个特征向量 作为后续支持向量机的输入向量，即：

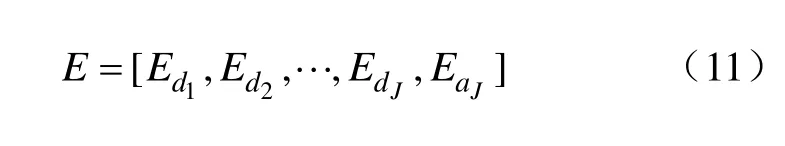
根据上述方法求出的6种扰动信号的能量分布特征向量差异较小，造成分类困难，因此首先用 E减去理想电压信号的能量分布特征向量Eref，得到能量差分布特征向量ΔE，然后把此向量作为 SVM 的输入向量。6层小波分解得到的是7维特征向量，6种电能质量扰动的能量差分布情况如图1所示。

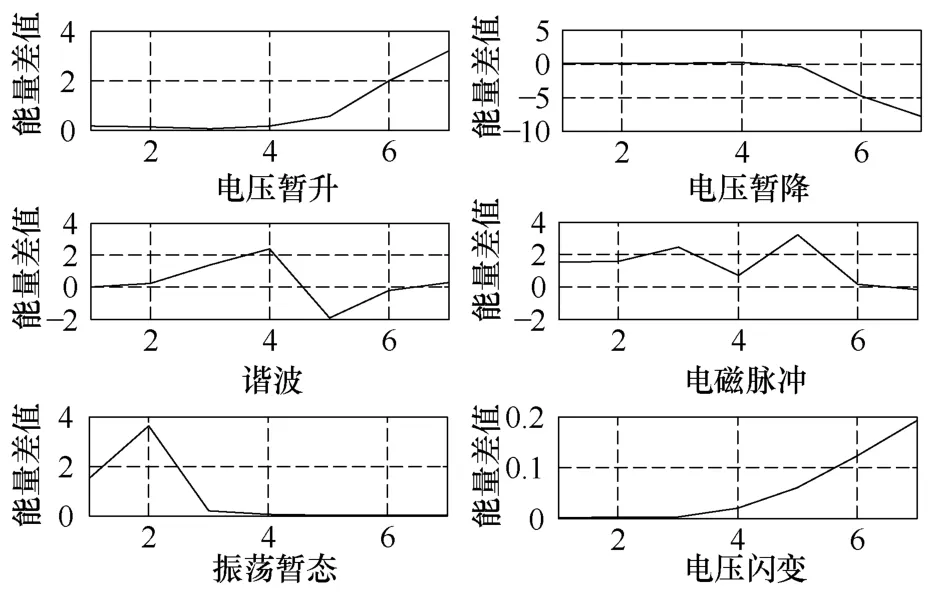
图1 6种电能质量扰动的能量差分布

2 支持向量机分类器

支持向量机（SVM）是针对分类和回归问题。

在小样本情况下提出的学习算法，它能把输入空间中线性不可分问题通过映射到高维空间，变成线性可分问题。通过建立一个超平面，使得正例和反例之间的隔离边缘被最大化[14]。

在二类模式分类问题中，SVM根据训练样本集(xi, yi)，i=1, 2, …, l（l为样本个数），由二次规划问题：

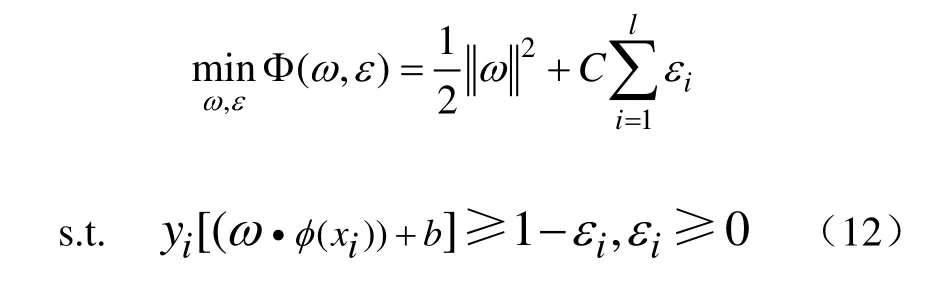
寻找最优分类超平面，其中，C为惩罚因子、ω为权向量，εi为松弛变量、b为分类阈值，φ (·)为非线性变换；由分类决策函数：

SVM是为解决二分类问题而设计的，不能直接用于解决多分类问题。而在实际应用中遇到的大多数为多分类问题，可以将多分类问题看成二分类问题的组合，最终将多分类问题转化为二分类问题。本文采用一对多（One-against-the rest）SVM这种多分类支持向量机[14]对6种电能质量扰动进行分类，SVM采用LibSVM和Matlab7.0共同建立。

3 仿真实验

3.1 小波分解层数对分类结果的影响

已有的文献对扰动信号做小波分解提取能量分布特征时一般做10层或者以上的小波分解，本文只做6层小波分解，可以减少特征提取时间和特征维数，以下通过实验来验证小波分解层数对扰动信号识别准确率的影响。本文实验中的支持向量机核函数选择高斯径向基核函数，即式中，σ为控制核函数宽度的高斯参数。通过交叉验证和网格搜索，高斯参数σ和惩罚因子 C分别取为10.56和32。

本文的扰动信号根据文献[13]中给出的数学模型随机产生。首先每种扰动信号在 20dB、30dB、40dB、50dB共 4种信噪比条件下各产生训练样本25个，即每种扰动训练样本100个，总的训练样本数是600个；然后提取7维的小波能量分布差向量ΔE，用来训练SVM。每种扰动测试样本1000个。6层小波分解和10层小波分解的6种电能质量扰动识别情况见表1。

表1 不同小波分解层数下的分类准确率对比

从表1可以看出，6小波分解的分类准确率略比10层小波分解的准确率高，6层是可以行的，并且可以减少特征提取时间，特征维数。

3.2 训练样本信噪比分布对分类结果的影响

采用SVM做分类时，首先要用训练样本对其进行训练。SVM的训练样本选择很重要，只有选择合适的训练样本才能增强其泛化能力，这样对未知样本的分类准确率才高。已有文献中SVM分类中通常只考虑某一信噪比条件下的训练样本。本文的每种扰动训练样本考虑以下两种SNR情况：①按3.1中添加分布比较均匀的4种SNR条件下的白噪声，每种SNR条件下的训练样本25个，即每种扰动信号训练样本100个；②只添加信噪30dB[3]条件下的白噪声，即每种扰动只添加单一信噪比条件下的噪声，每种扰动信号训练样本100个。因此情况①和情况②下每种扰动训练样本个数相同。两种SNR条件下扰动识别准确率对比实验的其他实验条件相同，且与3.1节相同，且只做6层小波分解。对比实验情况如表2所示，表2中每种SNR条件下每种测试样本1000个。

表2 训练样本不同信噪比分布时分类准确率对比

从表2可以看出，情况①的分类情况好于情况②，因此训练样本添加在较大范围内分布比较均匀的白噪声时，支持向量机的范化能力较强，特别是添加低信噪比的噪声；同时表2中情况②，测试样本在20dB情况下的分类准确率为 58.58%，因为训练样本中没有涵盖 20dB的噪声。分类结果很不理想，可能还由于高斯参数σ和惩罚因子 C同 3.1选择为32和10.56的结果；如果按照一般情况下选择σ和C分别选择为 1和 100，则训练样本不同信噪比分布时分类对比结果如表3所示。

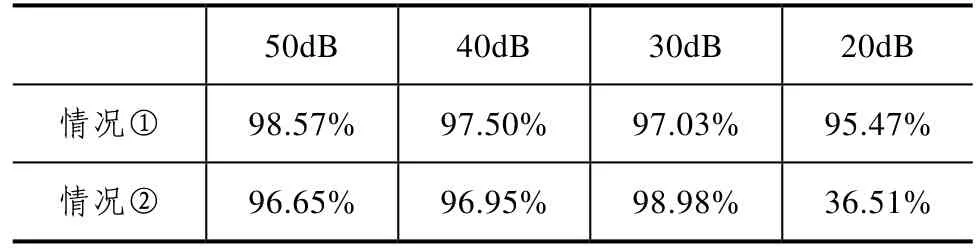
表3 训练样本不同信噪比分布时分类准确率对比

从表3同样可以看出，当训练样本信噪比较大范围内分布比较均匀时，支持向量机的范化能力较强，和表2的情形一样，因此表明了本文中增强SVM范化能力，提高分类准确率的措施是有效的。

4 结论

改进了基于小波能量差分布和 SVM 的电能质量扰动识别方法，在特征提取过程中，根据信号采样率确定小波分解层次，减少了特征提取时间，但是没有降低扰动信号的识别准确率。SVM 做分类时，采用信噪比较大范围内分布较均匀的训练样本来训练SVM，增强了SVM的范化能力，从而提高了扰动的识别准确率。仿真实验表明改进的方法的有效性，在信噪比低至20 dB时的分类准确率仍能达到95.20%。

[1] 覃思师,刘前进.基于STFT变换和DAGSVMs的电能质量扰动识别[J].电力系统保护与控制, 2011, 39(1):83-86, 103.

[2] 赵凤展,杨仁刚.时频分析方法在电能质量扰动检测与识别中的应用[J].华北电力大学学报, 2006, 33(5):33-37.

[3] 陈珍萍,欧阳名三,刘淮霞.小波能量差分布和SVM结合的PQD识别[J].计算机工程与应用, 2011, 47(20):241-244.

[4] 秦英林,田立军,常学飞.基于小波变换能量分布和神经网络的电能质量扰动分类[J].电力自动化设备,2009, 29(7): 64-67.

[5] 胡为兵,李开成,张明,等.基于小波变换和分形理论的电能质量扰动监控系统[J].电网技术, 2008, 32(12):51-55.

[6] 罗滇生,何洪英,姚建刚.短时电能质量分类方法研究[J].计算机工程与应用, 2008, 44(17): 238-241.

[7] LU G Y, FANG Q P. Classification of power quality disturbances using RVM and S-transform[J]. High Voltage Engineering, 2010, 36(10): 2565-2569.

[8] BISWAL B, PANIGRAHI B K. Power quality disturbance classification using fuzzy C-Means algorithm and adaptive particle swarm optimization[J].IEEE Transactions on Industrial Electronics, 2009,56(1): 212-220.

[9] LIAO Y, LEE J B. A fuzzy-expert system for classifying power quality disturbances[J]. International Journal of Electrical Power & Energy Systems, 2004,26(2): 199-205.

[10] 刘慧,刘国海,沈跃.采用提升小波包和相关向量机的电能质量扰动分类[J].高电压技术, 2010, 36(3):782-788.

[11] 许童羽,朴在林,陈春玲.提升小波在暂态电能质量扰动检测与定位中的应用[J].农业工程学报, 2011,27(5): 282-286.

[12] 赵静,何正友,王丽霞,等.基于数学形态学与动态时间扭曲的电压扰动分类[J].西南交通大学学报, 2009,44(2): 208-214.

[13] 张斌,孙静.基于 Mallat算法和快速傅里叶变换的电能质量分析方法[J].电网技术, 2007, 31(19): 35-40.

[14] 郑勇涛,刘玉树.支持向量机解决多分类问题研究[J].计算机工程与应用, 2005, 30(23): 190-192.