有限元法计算三相管型母线的短路电动力

廖宝文 曾 奕 杨皓宇

（1.上海交通大学电子信息与电气工程学院电气工程系，上海 200030；2.河北工业大学电气工程学院，天津 300130）

母线是电站内部的电力线路，它连接着各种电机和电器，以及传输电流和功率，并通过配电装置分配电能。由于管型母线的肌肤效应小，提高了载流量，因此目前大量使用管型母线。

当母线发生短路故障时，短路电流比正常工作电流大许多倍，产生巨大的力效应。不仅危及母线系统本身的运行，而且给整个电力系统的安全稳定带来了隐患。为了避免母线导体收到过大的电动力而发生形变或损坏，精确的计算短路电动力至关重要。

传统的方法采用的是公式法来计算母线的电动力，这种方法所计算的母线电动力与实际母线所受电动力存在一点偏差，为了得到较精确的结果，本文用有限元法来求解电磁场微分方程，以求得场量、电流和电动力。

1 管型母线短路电动力的计算

一般三相管型母线的排列形式是三根管型母线导体在同一平面内相互平行，这种形式是计算短路电动力的基础。三相管型母线通过50Hz的交流电，电流以相量形式给出，即

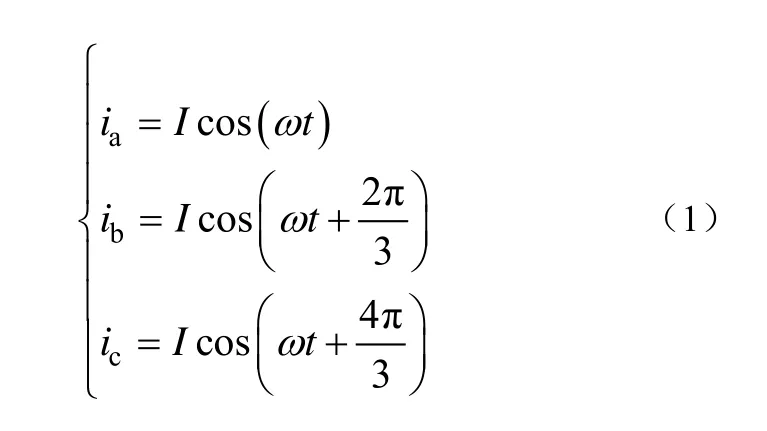
式中，I为短路电流有效值。假设短路故障为三相对称短路，因为三相对称短路的电动力最大。母线相间距离远远小于导体长度，这样母线导体可被视为无限长。母线材质为铜或者铝。

1.1 按照设计手册电动力计算公式计算

短路时母线所受电动力取决于母线导体的几何排列和外形尺寸。可以证明，当三相母线导体敷设在同一平面内，中间母线导体所受到的短路电动力最大，其受力为式中，a是相间距离（cm）。F是所产生的电动力（N）。Kfm为形状系数，在实际计算中，不论导体截面形状如何，只要当导体间距足够大时就可取Kfm=1，例如配电装置各相母线的间距有几百毫米便可取为1。

1.2 有限元方法计算

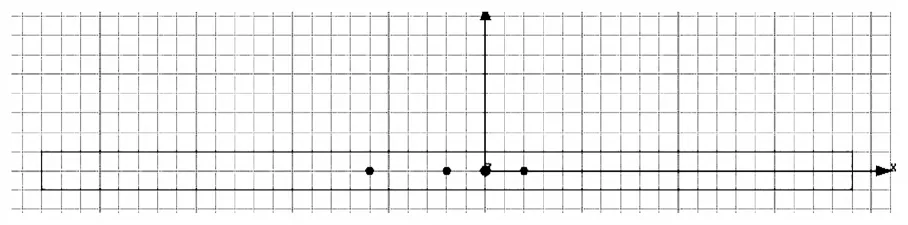
图1 三相母线在X-Y平面上的模型

如图1所示，在Ansoft Maxwell中建立在X-Y平面的 2D模型，三相母线通过三相电流，相位相差120°。

如图1所示，母线截面位于X-Y平面内，矢量磁位Az满足二维电磁场微分方程式（3）

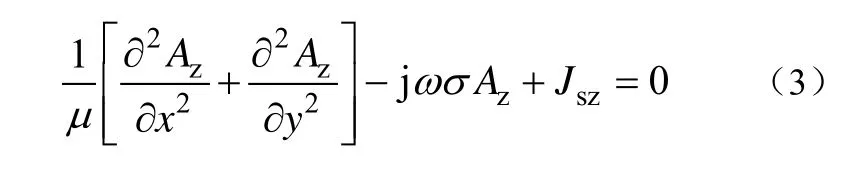
其中 - jω σAz+ Jsz= Jz。

式中，Jsz为源电流密度；Jz为z方向的全电流密度，

将管型母线截面离散化后如图 2所示，在 X-Y平面内对进行网格剖分，使用剖分方法为母线及其周围剖分密度大，网格较小，远离母线的地方网格较大，这样子剖分可以提高计算速度的同时又可以不影响计算精度。图3为母线附近较精密的网格剖分，从图3中可以看到，离母线越近，剖分越细致。

图2 三相母线在X-Y平面上的整体网格剖分模型

图3 三相母线在X-Y平面上的局部网格剖分模型

将管型母线截面离散化后，经过有限元分析计算，可求得离散区域内每个节点矢量磁位Az和源电流密度Jsz的值。因此，对于任意一个单元e中的涡流密度可以由式（4）得到

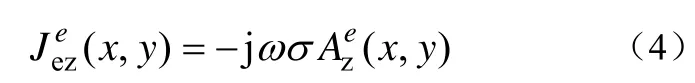
式中，对任一导体截面积的积分就是通过这一导体的全电流。

为了计算作用在每个单元导体上的电动力，必须求得单元e内的磁通密度。磁通密度可由矢量磁位的分布按下面的关系求得

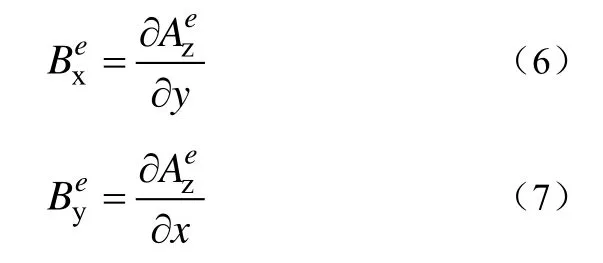
设体积元 dv内的全电流密度为 J，作用在 dv上的力dF为

因电流密度仅只有z方向的分量，所以磁通密度B位于整个X-Y平面。又由于对称性，电动力只有x方向的分量，故i相导体单元e所受到的电动力为

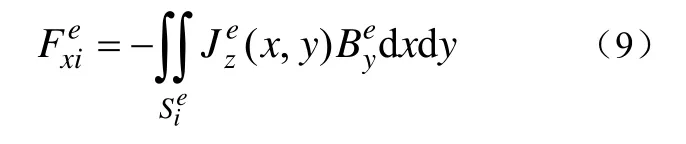
将单元e中的磁通密度视为常数，并且把单元e中的全电流 Ie和磁通密度写成向量形式带入式10得单元e所受

x方向力的时间函数

所有单元所受 x方向力之和，即为导体 i所受电动力为

2 计算机仿真计算机数据分析

2.1 参数的选择

几种硬导体的最大允许应力选择如下：铝（AL）：700kg/cm2；铜（Cu）：1400kg/cm2，母线相间距离为40cm，母线跨距为250cm。

2.2 计算结果

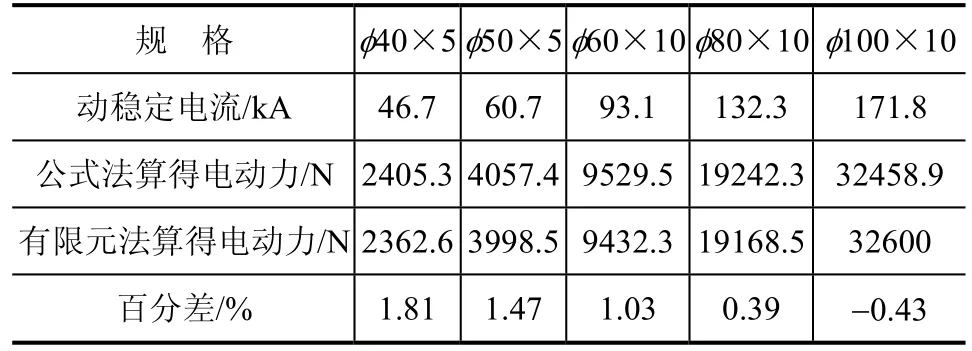
表1 铜管型母线电动力对比

表2 铝管型母线电动力对比

从表1、表2可以看出，不管对于铜母线还是铝母线，管径越小，公式法计算的结果误差越大，而且是正误差，即公式法的结果会比较大。而管径增大到一定程度，公式法的计算结果会比有限元法小，而且随着管径的增大误差越来越大。

3 结论

在计算三相管型母线短路电动力时，在管径较小时，即铜母线和铝母线管径在100mm以下，有限元法所得的结果始终要比设计手册中公式法所得的结果要的小更接近导体的实际受力，这对于母线的设计更为经济；而在管径达到 100mm及以上时候，有限元法算得的电动力比设计手册的公式法来的大，这时如果采用公式法所设计出来的母线可能会不能满足要求，这时候最好能过采用有限元法。

[1] 弋东方,钟大文.电力工程设计手册[M].北京:水利水电出版社, 1985.

[2] 吴励坚.大电流母线的理论基础与设计[M].北京:水利水电出版社, 1985.

[3] 《钢铁电力设计手册》编委会.钢铁电力设计手册[M].北京:冶金工业出版社, 1996.

[4] 赵博,张洪亮,等. Ansoft 12在工程电磁场中的应用[M].北京:中国水利水电出版社, 2010.