发电量提升技术在兆瓦级风力发电机组中的应用

丁 祥 兰志杰

（广东明阳风电产业集团有限公司, 广东 中山 528437）

风电作为一种可再生的绿色能源当前在电网中所占的比例越来越大。现有的变速运行风力机以其理论上能最大限度地实现最大风能捕获的优点正在并一直备受国内外学者的青睐，在过去的几十年里发展出了许多理论，诸如最大功率点跟踪MPPT算法等，也有一些有关转换效率的理论研究文[1]证明变速风力发电系统比恒速系统效率要高38%。然而到目前为止也没有实验能证明某个系统能一直捕获最大风能，这说明了风力发电系统本身具有一种不确定性。

目前，全国范围内可利用的低风速资源面积约占全国风能资源区的68%，且均接近电网负荷的受端地区。在风能资源较好地区的风电开发受限于并网瓶颈而不断“弃风”的背景下，低风速区风场开发逐渐引起各方关注。因此，进一步推进了机组发电性能的提升，为低风速风场客户创造了价值就显得尤为迫切。低风速机组由于其额定风速低，若要达到与普通机组同样的功率输出，就必须加大叶片以捕获更多的风能。

受多种因素的影响，传统变速恒频变桨矩风力发电机组往往没有运行在最佳CP-λ曲线上，也就是说未能真正实现理论上的最大风能捕获，尽管应用了类似最大功率点跟踪MPPT算法。

本文提出的低风速微调桨叶提升发电量技术能在不增加成本的基础上，充分发挥叶片空气动力学固有性能，在风电机组运行在低于额定转速时，通过桨叶调节维持最佳叶尖速比，追踪最大风能利用系数来实现最大风能捕获，从而达到提高风电机组发电量的目的。

1 微调桨叶控制算法

1.1 风能利用系数CP

通常，我们将风力涡轮机从自然风能中吸取能量的大小程度用风能利用系数CP来表示：

式中，PM为风力涡轮实际获得的轴功率；ρ为空气密度；A为叶轮的扫风面积；υ为叶轮的上游风速。

CP表示了风电机组将风能转化成电能的转换效率。根据贝兹（Betz）理论可以推导得出理论最大值为：CPmax=0.593。风能利用系数大小与叶尖速比和桨叶节距角有关系，如图1所示。

图1 叶片厂家提供的CP-λ曲线示意图

一个机组的Cpmax大小在很大程度上取决于叶片的翼型，叶片的工艺等，而一旦叶片成形后，Cpmax将无法改变。一般情况下，Cpmax取值范围为[0.45,0.49]。

1.2 最佳CP推导

为了表示风轮在不同风速中的状态，用叶片的叶尖圆周速度（线速度）与风速之比来衡量，称为叶尖速比，用λ来表示如下：

式中，ω为叶轮角速度，R为叶轮半径，N为叶轮转速，n为发电机转速，G为齿轮箱变比，υ为风速。

为了使机组产生最大的机械功率，应使CP达到其最大值CPmax不变，当风速变化时就必须使机组的转速随风速正比变化，即有多大风速才能驱动多大的转速，并保持一个恒定的最佳叶尖速比λopt，由（2）式可得

因而，由式（1）可得机组最大输出功率：

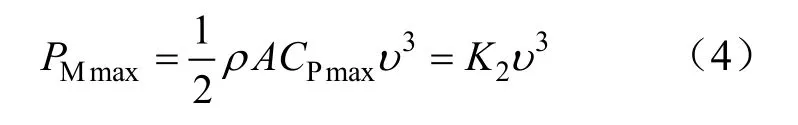
根据λ与CP的关系及CP与PM之间关系，在风速固定时，不同的转速即对应不同的λ，对应不同的CP，对应不同的PM，若设定不同的风速，就可以得到机组在不同风速下PM与转速的关系，机组输出的PMmax与风速的三次方成正比，也与转速的三次方成正比。

因此，在按λopt或按PMmax运行的情况下，机组在各种风速下均可以保持CPmax不变，有下列关系式成立：

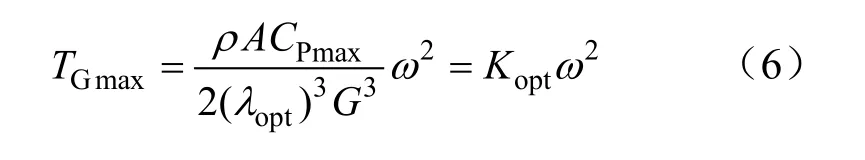
式中，TW为叶轮转矩，Ω为叶轮角速度，TG为发电机转矩，n为发电机角速度，在ρ不变时为常数。

由式（6）可知，Kopt受到空气密度ρ的影响，当ρ变化时，若继续维持λopt运行，则需动态调整Kopt跟上ρ的变化，实现CPmax。

1.3 追踪最佳CP

当风机运行在低于额定转速区间时，通过调节桨叶桨距角来控制叶轮转速，维持λopt，追踪CPmax来捕获最大的风能，从而提高风机的实时发电功率。由图1可知，为了实现最大风能捕获，成功追踪CPmax，就要将λ区间分段处理，取每一段λ区间对应的最大风能利用系数曲线，此时对应的桨叶角度即为所调。理论上，要将λ区间分为无穷小段，每一微元段对应的风能利用系数为此段最大值，对应的桨叶角度也是去穷多个。事实上，桨叶角度的调节是需要一定的响应时间和足够的动作时间，因而实际上为了防止叶片的频繁变桨给变桨系统带来的不良影响，我们一般将λ区间分为3段来处理。

设定三个桨叶工作区间，λn1和λn2分别为桨距角分别为α1、α2和α3时对应CP-λ曲线的交点。根据λn1和λn2来划分桨叶实际工作区间，即

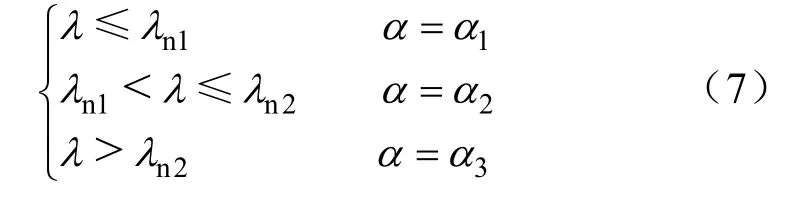
如图2所示，在λ＞λn1时，将桨距角调节到α2让机组CP从曲线 1运行到曲线 2上以获得更大的CP；同样，在λ＞λn2时，将桨距角调节到α3让机组CP从曲线2运行到曲线3上以获得更大的CP，从而达到提升机组发电量的目的。

图2 典型CP-λ曲线

由于两个λ值的临界点的存在，若是风速较小且不稳定，λ值在小区间[-0.5, 0.5]内不停变动，导致频繁变桨，所以必须选取合理的λ值，真正识别是否需要进行变桨调节。

为避免桨叶频繁动作，需在CP-λ曲线的交点λn1和λn2处设置一个回滞区间值。

2 仿真分析

为了验证控制策略的可靠性和有效性，以明阳MY1.5型双馈风力发电机组为对象搭建模型进行仿真分析，额定功率1500kW，额定电压690V，额定转速1750r/min，切入风速3m/s，切出风速25m/s，取标准空气密度（ρ=1.225kg/m3），额定风速10.8m/s，仿真结果如图3、图4所示。

由不同桨距角对应的CP-λ曲线可知，当风速ν＜5m/s时，风轮转速Ω不变，则风速v越小，叶尖速比λ越大，此时大桨距角对应的CP反而变大。根据当前风速值调整最佳桨距角（通常情况下为0°）为[0°, 1.5°]。

如图3所示，仿真结果表明当机组运行在ν＜5m/s风速段时，桨叶角度α[0°, 1.5°]越大，功率曲线越好，桨叶角度从0°调到0.5°提升效果较好，提升比例约为3%，再继续增大桨叶角度α，功率提升效果并不明显。

如图4所示，仿真结果表明当机组运行在风速8＜v＜11m/s风速段时，桨叶角度[-1.5°, 0°]越小，功率曲线越好，桨叶角度从 0°调到-0.5°提升效果较好，提升比例约为3%，再继续减小桨叶角度α，功率提升效果并不明显。

图3 风速（ν＜5m/s）微调桨叶功率曲线对比

图4 风速（8m/s ＜ν＜11m/s）微调桨叶功率曲线对比

3 现场测试及结果分析

为了验证控制算法在实际运行中对发电量的提升效果，我们分别在华能南方某风场和大唐北方某风场进行了现场测试。

南方某风场选用66台明阳MY1.5S型南方抗台风型双馈风力发电机组，选取其中的3台机组进行了现场测试。

图5 南方某风场测试前后功率曲线对比

初步测试结果表明发电量提升比例大约为2.22%。

北方某风场选用267台明阳风电MY1.5Se型北方低温型风电机组，选取其中的4台机组进行了现场测试。

图6 北方某风场测试前后功率曲线对比

初步测试结果表明发电量提升比例大约为2.57%。

4 结论

本文针对低风速地区风电场提升发电量的紧迫需求，制定了通过微调桨叶来捕获最大风能的控制策略，并通过仿真分析和现场测试验证了该控制策略的可靠性和有效性，为低风速地区发电量提升技术的研究提供了参考。

[1]叶杭冶.风力发电机组的控制技术[M].北京： 机械工业出版社, 2006.

[2]ZINGER D S, MUJADI E.Annualized wind energy improvement using variable speeds[J].IEEE Trans.on Ind.Appl, 1997, 33： 1444-1447.

[3]刘剑, 李建林, 潘磊, 等.最大风能捕获策略研究[A].中国电工技术学会电力电子第十届年会, 西安,2006.9： 24-26.

[4]刘其辉, 贺益康, 赵仁德.变速恒频风力发电系统最大风能追踪控制[J].电力系统自动化, 2003,27(20)： 62-67.